Указания по технике безопасности. При выполнении работы студенты должны руководствоваться общими для учебных аудиторий правилами техники безопасности.

При выполнении работы студенты должны руководствоваться общими для учебных аудиторий правилами техники безопасности.

Методика и порядок выполнения работы

Получить вариант задания (таблица 6.1).

Таблица 6.1 – Исходные данные

Вари-ант	Целевая функция и ограничения	Вари-ант	Целевая функция и ограничения

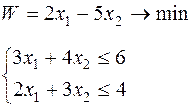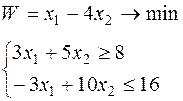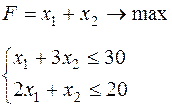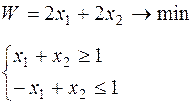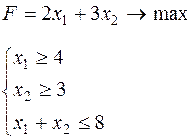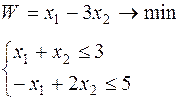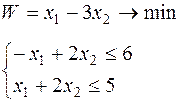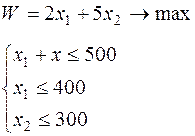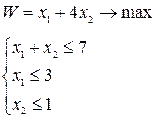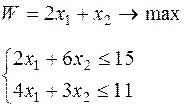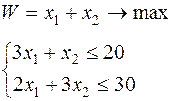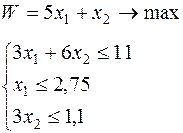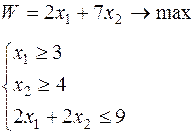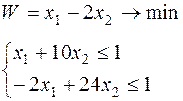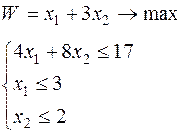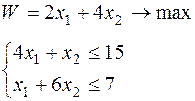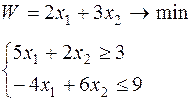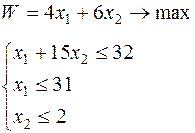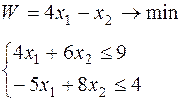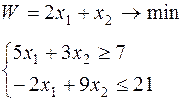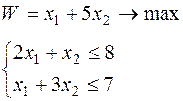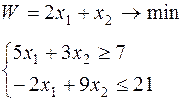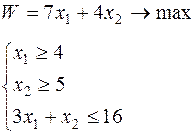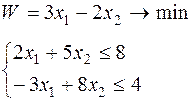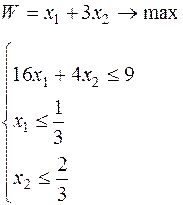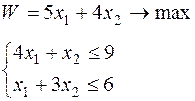Во всех задачах .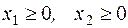

Порядок выполнения рассмотрим на примере решения задачи геометрическим способом.

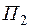Предприятие изготавливает два вида продукции и , которая поступает в оптовую продажу. Для производства продукции используются два вида сырья А и В. Максимально возможные запасы сырья в сутки составляют 9 и 13 единиц соответственно. Расход сырья каждого вида на единицу продукции вида 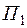и вида 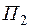приведены в таблице 6.2

Таблица 6.2 – Данные о расходе сырья

Сырье	Расход сырья на единицу продукции, ед.	Запас сырья,
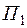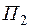			ед.
А
В

Опыт работы показал, что суточный спрос на продукцию 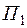никогда не превышает спроса на продукцию 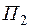более чем на 1 единицу. Кроме того, известно, что спрос на продукцию 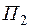никогда не превышает 2 единицы в сутки.

Оптовые цены единицы продукции равны 3 у. д. е. для 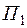и 4 у. д.е. для .

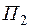Какое количество продукции каждого вида должно производить предприятие, чтобы доход от реализации продукции был максимальным?

Решение

Построим многоугольник решений (рисунок 6.5). Для этого в системе координат Х1OХ2на плоскости изобразим граничные прямые:

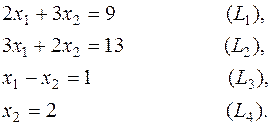
Взяв какую-либо точку, например, начало координат, установим, какую полуплоскость определяет соответствующее неравенство. Полуплоскости, определяемые неравенствами, на рисунке 6.5 показаны стрелками. Областью решений является многоугольник ОАВСD.

Для построения прямой 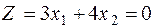строим вектор-градиент 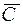=(3;4) и через точку 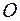проводим прямую, перпендикулярную ему. Построенную прямую Z=0 перемещаем параллельно самой себе в направлении вектора 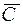. Из рисунка 6.5 следует, что опорной по отношению к многоугольнику решений эта прямая становится в точке 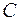, где функция принимает максимальное значение. Точка 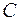лежит на пересечении прямых 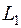и 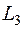. Для определения ее координат решим систему уравнений:

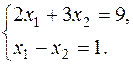
Оптимальный план задачи 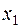=2,4; 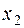=1,4. Подставляя значения 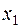и 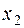в линейную функцию, получаем:

.

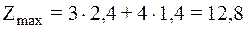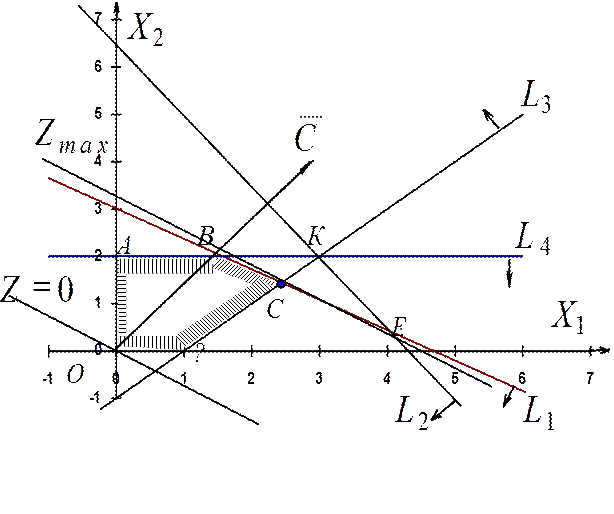
Рисунок 6.5 – Графическое решение задачи

Полученное решение означает, что объем производства продукции 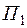должен быть равен 2,4 единицы, а продукции 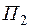– 1,4 единицы. Доход, получаемый в этом случае, составит Z=12,8 у. д. е.

Содержание отчета и его форма

Отчет должен содержать:

6.1 Прямые уравнений, вектор 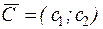,прямую ;

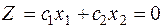6.2 Многоугольник решений;

6.3 Координаты точки максимума функции и вычислить значение целевой функции в этой точке;

6.4 Выводы.

Контрольные вопросы и защита работы

7.1 Что необходимо для практического решения задачи линейного программирования?

7.2 Какие частные случаи встречаются при решении задачи линейного программирования графическим методом?

7.3 Что определяет целевая функция на плоскости?

7.4 Что может быть областью допустимых решений в задаче линейного программирования при решении ее графическим методом?

Защита работы проводится в устной форме, состоит в предоставлении студентом правильно выполненного отчета по работе, коротком докладе и в ответах на вопросы, представленные выше.

Практическое занятие 18.

Симплексный метод решения задачи

Цель и содержание

Цель работы – приобрести навыки решения задач линейного программирования симплекс-методом.

В результате выполнения работы студенты должны:

1. Привести задачу к виду, допускающему применение симплекс-алгоритма;

2. Составить симплекс-таблицу;

3. Найти оптимальное решение;

4. Сделать выводы.

Теоретическое обоснование

Общая идея симплекс-метода.Для начала работы требуется, чтобы заданная система ограничений выражалась равенствами, причем в этой системе ограничений должны быть выделены базисные неизвестные. Решение задачи при помощи симплекс-метода распадается на ряд шагов. На каждом шаге от данного базиса 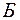переходят к другому новому базису 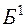c таким расчетом, чтобы значение функции 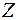уменьшалось, т. е. 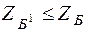. Для перехода к новому базису из старого базиса удаляется одна из переменных и взамен нее вводится другая из числа свободных. После конечного числа шагов находится некоторый базис 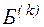, для которого 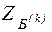есть искомый минимум для линейной функции 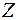, а соответствующее базисное решение является оптимальным, либо выясняется, что задача не имеет решения.

Алгоритм симплекс-метода

Рассмотрим систему ограничений и линейную форму вида:

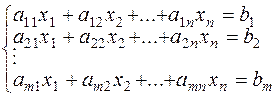	(7.1)
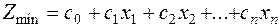	(7.2)
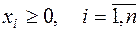	(7.3)

Используя метод Жордана-Гаусса, приведем записанную систему к виду, где выделены базисные переменные.

Условные обозначения:

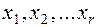– базисные переменные;

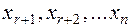– свободные переменные.

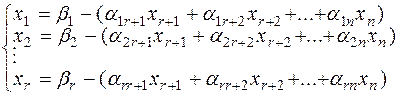	(7.4)
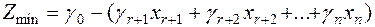	(7.5)

По последней системе ограничений и целевой функции 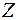построим таблицу вида:

Базисные	Свободные
Свобод­ный член			...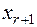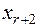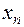
				...
				...
...	...	...	...	...	...
				...
				...

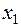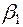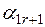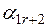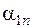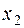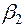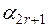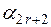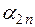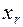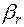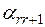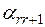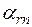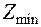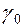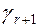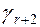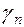Данная таблица называется симплекс-таблицей. Все дальнейшие преобразования связаны с изменением содержания этой таблицы.

Алгоритм симплекс-метода сводится к следующему:

1. В последней строке симплекс-таблицы находим наименьший положительный элемент, не считая свободного члена. Столбец, соответствующий этому элементу, считается разрешающим.

2. Вычисляют отношение свободных членов к положительным элементам разрешающего столбца (симплекс-отношение). Находят наименьшее из этих симплекс-отношений, оно соответствует разрешающей строке.

3. На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент.

4. Если имеется несколько одинаковых по величине симплекс - отношений, то выбирают любое из них. То же самое относится к положительным элементам последней строки таблицы.

5. После нахождения разрешающего элемента переходят к следующей таблице. Неизвестные переменные, соответствующие разрешающей строке и столбцу меняют местами. При этом базисная переменная становится свободной переменной и наоборот.

Базисные	Свободные
Свобод-ный член			...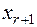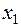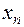
				...
				...
...	...	...	...	...	...
				...
				...

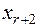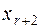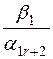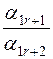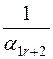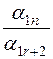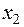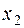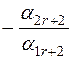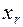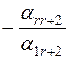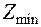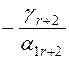6. Элемент таблицы 2, соответствующий разрешающему элементу таблицы 1, равен обратной величине разрешающего элемента.

7. Элементы строки таблицы 2, соответствующие элементам разрешающей строки таблицы 1, получаются путем деления соответствующих элементов таблицы 1 на разрешающий элемент.

8. Элементы столбца таблицы 2,соответствующие элементам разрешающего столбца таблицы 1, получаются путем деления соответствующих элементов таблицы 1 на разрешающий элемент и берутся с противоположным знаком.

9. Остальные элементы вычисляются по правилу прямоугольника: мысленно вычерчиваем прямоугольник в таблице 1, одна вершина которого совпадает с разрешающим элементом, а другая с элементом, образ которого мы ищем; две другие вершины определяются однозначно. Тогда искомый элемент из таблицы 2 будет равен соответствующему элементу таблицы 1 минус дробь, в знаменателе которой стоит разрешающий элемент, а в числителе – произведение элементов из двух неиспользованных вершин прямоугольника.

10. Как только получится таблица, в которой в последней строке все элементы отрицательны, считается, что минимум найден. Минимальное значение функции равно свободному члену в строке целевой функции, а оптимальное решение определяется свободными членами при базисных переменных. Все свободные переменные в этом случае равны нулю.

11. Если в разрешающем столбце все элементы отрицательны, то задача не имеет решений (минимум не достигается)

Аппаратура и материалы

Микрокалькулятор, программное обеспечение MS Excel.