Предел последовательности
Число а называется пределом последовательности (хn), если для любого положительного числа  найдётся такой номер
найдётся такой номер  (зависящий от
(зависящий от  ), что, начиная с этого номера (т.е. для всех
), что, начиная с этого номера (т.е. для всех  ), будет выполняется неравенство
), будет выполняется неравенство
 (1)
(1)
Обозначают:
 .
.
Последовательность, имеющая предел, называется сходящейся, а не имеющая предела – расходящейся. Геометрическая интерпретация предела: если число а является пределом последовательности (хn), то в произвольную, сколь угодно малую  -окрестность точки а, попадают все члены данной последовательности начиная с некоторого номера
-окрестность точки а, попадают все члены данной последовательности начиная с некоторого номера  .
.
Всякая сходящаяся последовательность является ограниченной.
Всякая монотонная и ограниченная последовательность сходится.
Если последовательность не является ограниченной, то она не имеет предела.
Если предел последовательности равен нулю, то её называют бесконечно малой.
Свойства бесконечно малых последовательностей:
1) сумма и произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью;
2) произведение ограниченной последовательности на бесконечно малую является бесконечно малой;
3) для того чтобы выполнялось равенство  , необходимо и достаточно, чтобы выполнялось равенство
, необходимо и достаточно, чтобы выполнялось равенство  , где
, где  – бесконечно малая последовательность.
– бесконечно малая последовательность.
Последовательность называется бесконечно большой, если для любого сколь угодно большого числа М найдётся такой номер  , что для всех n, начиная с этого номера
, что для всех n, начиная с этого номера  , выполняется неравенство
, выполняется неравенство
 .
.
Если последовательность (хn) – бесконечно большая, то говорят, что она стремится к бесконечности, и пишут  .
.
Последовательность не имеет предела в 2-х случаях:
1) предел не определён;
2) последовательность является бесконечно большой.
Если 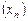 - бесконечно большая последовательность, то
- бесконечно большая последовательность, то  – бесконечно малая последовательность.
– бесконечно малая последовательность.
Если 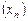 – бесконечно малая последовательность, то
– бесконечно малая последовательность, то  – бесконечно большая.
– бесконечно большая.
Если последовательности 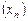 ,
,  имеют пределы, то справедливы следующие свойства:
имеют пределы, то справедливы следующие свойства:
1)  где
где  ;
;
2)  ;
;
3)  ;
;
4)  где
где  .
.
Свойства 2) и 3) обобщаются, соответственно, на любое конечное число слагаемых и множителей.
При вычислении пределов числовых последовательностей могут возникнуть неопределённости вида 
 . Для того чтобы вычислить предел в случае неопределенности, необходимо тождественно преобразовать выражение, стоящее под знаком предела.
. Для того чтобы вычислить предел в случае неопределенности, необходимо тождественно преобразовать выражение, стоящее под знаком предела.
Пример 1. Пользуясь определением предела последовательности, доказать, что  .
.
Решение. Выбираем произвольное число  . Согласно определению, число 3 является пределом последовательности
. Согласно определению, число 3 является пределом последовательности 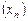 , если сможем указать такой номер
, если сможем указать такой номер  , что для всех членов последовательности с номерами
, что для всех членов последовательности с номерами  выполняется неравенство (1), которое в нашем случае имеет вид
выполняется неравенство (1), которое в нашем случае имеет вид
 . (2)
. (2)
Неравенство (2) равносильно неравенству
 ,
,
т.е.
 или
или  .
.
Поскольку  и
и  , из последнего неравенства получаем
, из последнего неравенства получаем
 ;
;  .
.
В качестве номера  члена последовательности, начиная с которого выполняется неравенство (2), может быть выбрано натуральное число
члена последовательности, начиная с которого выполняется неравенство (2), может быть выбрано натуральное число
 .
.
Этим мы доказали, что существует номер члена последовательности, начиная с которого выполняется неравенство (1) для заданной последовательности. Значит, число 3 – предел этой последовательности.
Пример 2. Вычислить предел последовательности:
1)  2)
2)  ;
;
3)  .
.
Решение. 1. Преобразуем выражение, стоящее под знаком предела, т.к. непосредственно вычисление приводит к неопределенности типа 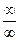 .
.

Разделим далее числитель и знаменатель дроби на старшую степень, т.е. на  и получим
и получим
 ,
,
так как при  последовательности
последовательности  стремятся к нулю.
стремятся к нулю.
Таким образом, приходим к ответу:
 .
.
2. Так как по определению факториала

 ,
,

то получаем

Делением на старшую степень выражения, т.е. на  , убеждаемся, что
, убеждаемся, что

3. Поскольку при  имеем
имеем  и
и  , то выражение
, то выражение  даёт неопределённость типа
даёт неопределённость типа 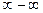 . Умножив и разделив выражение
. Умножив и разделив выражение  на сопряжённый множитель
на сопряжённый множитель  , получим:
, получим:

Разделим числитель и знаменатель на старшую степень, т.е. на  тогда
тогда

Таким образом, получаем ответ:

