Несобственные интегралы

Если функция f(x) непрерывна при 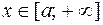, то несобственным интегралам 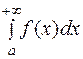называется 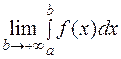. Если этот предел существует и конечен, то интеграл называется сходящимся. В противном случае интеграл называется расходящимся.

Аналогично определяются интегралы

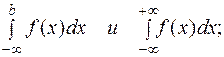
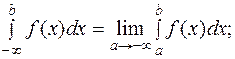
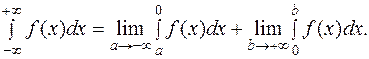
Если функция f(x) непрерывна при 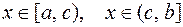и имеет разрыв II рода в точке c, то несобственным интегралом 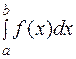называется

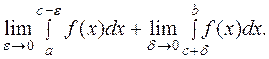
Так же, как и выше, несобственный интеграл называется сходящимся, если оба предела существуют и конечны. В противном случае несобственный интеграл называется расходящимся.

Если же точка разрыва находится в конце промежутка, то:

в) при c=a

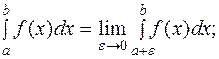
г) при c=b

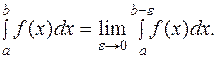
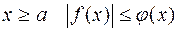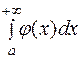Если при и сходится, то 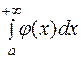сходится. Такая сходимость называется абсолютной.

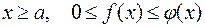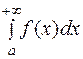Если при и расходится, то 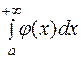расходится.

Если при 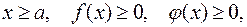предел 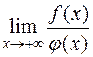конечен и не равен нулю, то оба интеграла 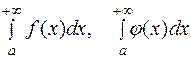одновременно либо сходятся, либо расходятся.

Аналогичные признаки сходимости можно указать и для несобственных интегралов от разрывных функций.

Р Я Д Ы

ВВЕДЕНИЕ

Настоящее пособие является кратким изложением свойств бесконечных рядов, а также представление функций в виде бесконечных рядов более простых функций. Последнее делает бесконечные ряды одним из важнейших численных методов в математике и находит широкое практическое применение.

Рядом в математике называется бесконечная сумма чисел или функций, составленная по определенному закону:

u₁ + u₂ + u₃ + … + u_n +……… (1),

где u_n - члены ряда; многоточие указывает на то, что выражение (1) не имеет последнего слагаемого, т.е. ряд – бесконечная сумма. Поэтому вместо (1), пользуясь знаком суммы, часто пишут так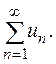

Числовые ряды

Ряд называется числовым, если члены этого ряда – числа u_n, которые задаются только функциями номера n, т.е. u_n = f(n). Последовательно складывая члены ряда, составим (в бесконечном количестве) суммы:

S₁ = u₁ , S₂ = u₁+ u₂ , …, S_n = u₁+ u₂+ u₃+…+ u_n

Их называют частичными суммами ряда.

Конечный или бесконечный предел S частичной суммы S_n ряда (1) при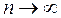

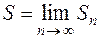(2)

называют суммой ряда и записывают

S = u₁+ u₂+ u₃+…+ u_n+… =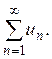

Если ряд имеет конечную сумму, то его называют сходящимся; в противном случае (т.е. если сумма равна ±¥, либо же суммы вовсе нет) – расходящимся.

Поясним понятие суммы ряда на конкретном примере. Пусть задан числовой ряд

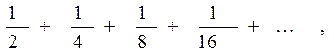(3)

каждый последующий член которого равен половине предыдущего.

Подсчитаем суммы одного, двух, трех, четырех, пяти его членов:

S₁ = ,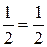

S₂ = ,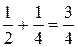

S₃ = ,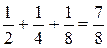

S₄ = ,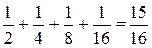

S₅ = .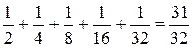

Значения этих сумм отличаются от 1 на 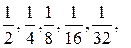т.е. при увеличении числа слагаемых получаем для их сумм значения все меньше отличающиеся от 1. Поясним сказанное на рис. 1.

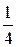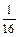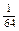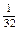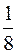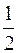Рис. 1

Прямоугольник площадью в одну квадратную единицу разобьем на два прямоугольника. Один из них вновь разобьем на два прямоугольника одинаковой площади. Продолжая этот процесс деления, получим прямоугольники, площади которых равны 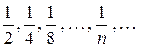квадратных единиц. Объединение этих прямоугольников приближает нас к исходному. Следовательно, и сумма их площадей приближается к площади исходного прямоугольника, т.е. к 1. Число 1 называют суммой ряда (3).

Пример 1.

u_n= 1, S_n = 1 + 1 + 1 + ¼ + 1 = n,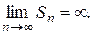

Пример 2.

u_n= (-1)ⁿ, S_n = - 1 + 1 - 1 + 1 – 1 + ¼ + (-1)ⁿ.

Такой ряд предела не имеет, т.к. его верхний предел равен 0, а нижний предел равен –1.

Пример 3.

u_n= u₁ q^n-1, S_n = u₁ + u₁ q + u₁ q² + ¼ + u₁ q^n-1.

Этот ряд – геометрическая прогрессия со знаменателем q – называется геометрическим рядом. Умножим S_n на q и вычтем полученное выражение почленно из S_n

S_n q = u₁ q + u₁ q² + u₁ q³ + ¼ + u₁ qⁿ,

S_n - S_n q = u₁ - u₁ qⁿ, S_n (1-q) = u₁ (1-qⁿ).

Для частичной суммы S_n геометрического ряда получаем

S_n = u₁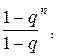

предел которого и представляет сумму геометрического ряда

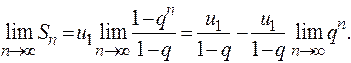
При |q| < 1, 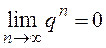и 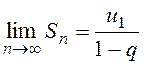, ряд сходится;

при |q| > 1 ряд геометрической прогрессии расходится;

при q = 1 см. пример 1;

при q = -1 см. пример 2.

Пример 4.

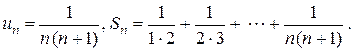
Запишем

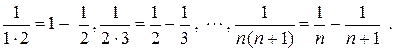
Представим сумму п членов исследуемого ряда в виде:

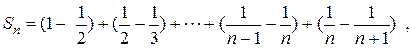
тогда 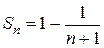и 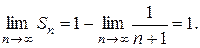Следовательно, ряд сходится.