Билет 40. Линейные дифференциальные уравнения порядка выше 1-го с постоянными коэффициентами и специальной правой частью

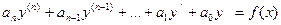
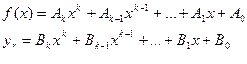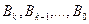а) , где методом неопределённых коэффициентов.

Б)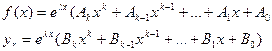

Если λ несовпадает с корнями характеристического уравнения.

В)Если λ совпадает с корнями хар-го уравнения .

s-степень кратности

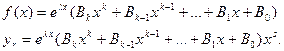
г )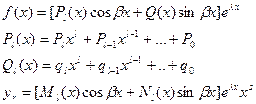

s- степень кратности.

Теорема:Если 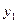-решение уравнения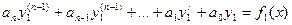

Если 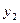-решение уравнения .

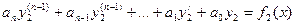Тогда y= 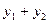-будет решением уравнения

.

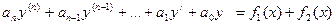Док-во: y= .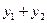

-

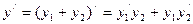
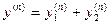
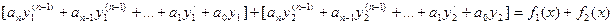Принцип суперпозиции.

Билет 41. . Основные понятия функции нескольких переменных

Если каждой паре (x,y) значений двух, независимых друг от друга , переменных величин x и y , из некоторой области их изменения D соответствует определённое значение величины z , то мы говорим, что z есть функция двух независимых переменных x и y, определённая в области D.

Обозначение:z=f(x,y), z=F(x,y) и т.д.

Совокупность пар (x,y) значений x и y , при которых определяется функция z=f(x,y), называется областью определения этой функции.

Область определения наглядно иллюстрируется геометрически. Если каждую пару значений x ,y мы будем изображать точкой M(x,y) в плоскости Oxy,то область определения функции изобразится в виде некоторой совокупности точек на плоскости.Эту совокупность называют также областью определения. Линию , ограничивающую данную область называют границей области. Точки, не лежащие на границе- внутренние.

Область, состоящая из одних внутренних точек –открытая или незамкнутая. Если к области относятся и точки границы , то область замкнутая.

Область называется ограниченной, если существует такое постоянное C, что расстояние до любой точки M области от начала координат O меньше С, т.е. |OM|<C.

Функция нескольких переменных может быть задана с помощью таблицы или формулы.

№43Непрерывность функции в точке

Пусть функция y=f(x) определена в некоторой окрестности

точки х₀.

Определение 1. Функция y=f(x) называется непрерывной в точке х₀, если для любого 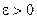найдется 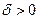такое, что при всех х, удовлетворяющих неравенству 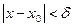, будет выполняться неравенство

.

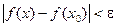Определение 2. Функция y=f(x) называется непрерывной на множестве АÌR, если она непрерывна в каждой точке множества А.

Сравнивая определение 1 с определением предела функции(Определение. Число А называется пределом функци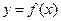и при 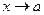, если для любого e>0 найдется 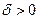такое, что при всех х, удовлетворяющих неравенству 0< 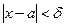, будет выполняться неравенство 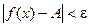. Кратко это можно записать так:

.

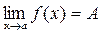), можно получить, что функция y=f(x) непрерывна в точке х₀ тогда и только тогда, когда ее предел при x ® х₀ равен значению функции в этой точке:

.

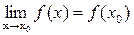Определение 3. Приращением аргумента называется разность двух значений переменной х и обозначается Dх. Приращением функции, соответствующим данному приращению аргумента, называется разность двух значений функции от соответствующих аргументов и обозначается Dу:

Dх=х-х_{0 ,} Dу=f(x)-f(x₀).

Из определения 1 следует:

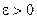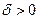" $ , для 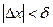будет выполняться 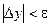, т.е.

.

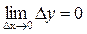Таким образом, функция непрерывна в точке тогда и только тогда, когда малому приращению аргумента соответствует малое приращение функции.

№44