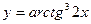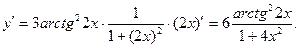Производная сложной функции. Пусть у = f(u) – функция от переменной u, а - функция от переменной х
Пусть у = f(u) – функция от переменной u, а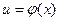 
- функция от переменной х, тогда 
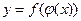- сложная функция.
Теорема.Если у = f(u) и 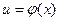- дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу u, умноженной на производную самого промежуточного аргумента по независимой переменной х, т.е. 
.
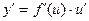Эта теорема распространяется и на сложные функции, которые состоят из нескольких вложенных функций. Например, если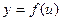 
, 
, 
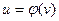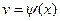, т.е. 
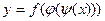, то 
.
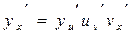Найти производные функций:
1) 
.
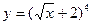Представим данную функцию как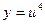 
, где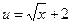 
, тогда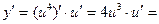 
= 
.
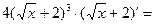
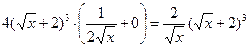2) 
.
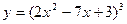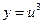, где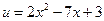 
, тогда
.
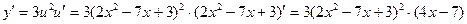Можно не вводить промежуточную переменную, а сразу находить производную по внешней функции, и умножать ее на производную внутренней функции:
. 
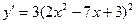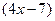
производная производная
степенной основания
ф-и степени.
3) 
.
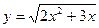Обозначим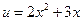 
; 
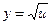, тогда 
.
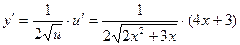4) 
.
; 
. 
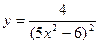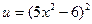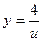Воспользуемся формулой (2) из таблицы, и результат умножим на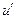 
. Видно, что обозначенная нами через 
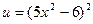функция сама является сложной: степенная функция, у которой основание тоже является функцией.
,
.
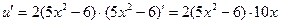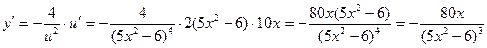Эту же производную можно найти другим способом. Перепишем условие:
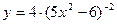, тогда как производная степенной функции:
.
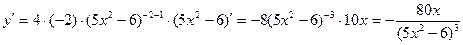5) 
.
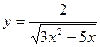Обозначим: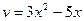 
; 
; 
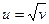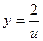, тогда 
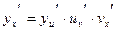, где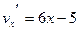 
; 
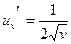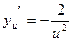, подставим:
.
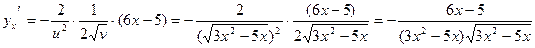Эту же производную можно найти другим способом. Перепишем условие:
.
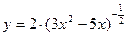
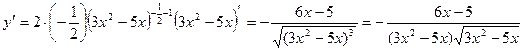Производная произведения и частного
Найти производные функций:
1) 
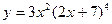
Обозначим через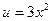 
; 
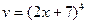, тогда y=u. v , т.е. нужно найти производную произведения двух функций. Применим формулу: 
;
; 
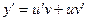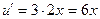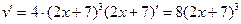, тогда 
.
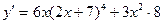2) 
; 
.
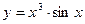
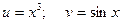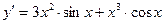3) 
.
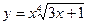
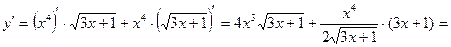
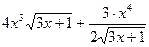4) 
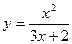
Имеем частное двух функций: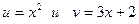 
. Согласно формуле для нахождения производной частного двух функций 
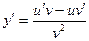, имеем:
.
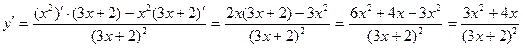5) 
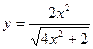
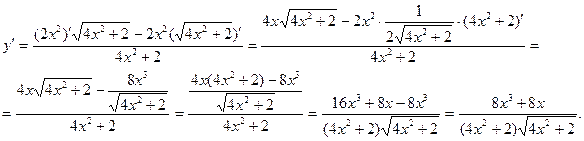
Производная тригонометрических функций
Найти производные функций:
1) 
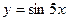
Имеем сложную функцию, в которой внешняя функция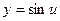 
, а внутренняя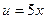 
По правилу дифференцирования сложных функций находим производную внешней функции и умножаем ее на производную внутренней:
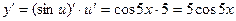
2) 
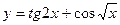
Имеем алгебраическую сумму двух сложных функций.
.
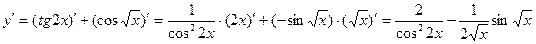3) 
.
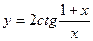
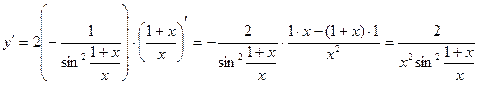4) 
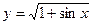
Сначала находим производную корня, и умножаем ее на производную подкоренного выражения.
.
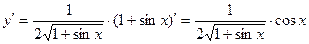5) 
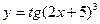
Имеем сложную функцию, состоящую из 3-х звеньев: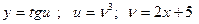 
;
;
.
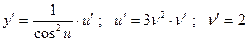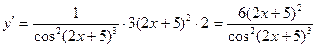6) 
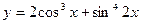
Имеем сумму двух сложных функций.
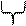
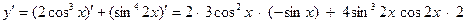
производная произв. произв. произв. произв.
степени косинуса степени синуса аргумента
7) 
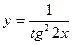
Перепишем: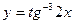 
. Тогда 
.
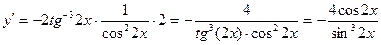8) 
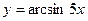
Нужно обратить внимание, что в формулу производной обратной тригонометрической функции вместо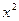 
нужно брать квадрат всей функции, которая стоит под знаком обратной тригонометрической функции, и еще умножить на производную этой функции.
.
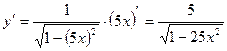9) 
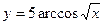
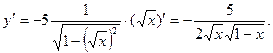
10) 
