Организационный момент
2. Проверка выполнения домашнего задания. (5 мин)
Подготовка к основному этапу. Актуализация. (5 мин)
Задача.
В полдень термометр показывал температуру t0C, а к полуночи температура опустилась на р0С. Какую температуру показывал термометр в полночь? Составьте выражение и найдите его значение: при t = 25, р = 7.
4. Усвоение новых знаний. (5 мин)
Термометр - это прибор, созданный человеком для измерения температуры. Температурой называют величину, которая показывает какое тепло имеет тело, (некоторый объект). Изменение тепла и температуры – это одно из явлений природы, которая изучает наука физика. Также физика изучает другие явления: движение, то есть механическое явление. Еще физика изучает электрические и магнитные явления, свойства света, которые называются оптическими явлениями. Благодаря открытиям в области физики, человечество имеет такую хорошо развитую технику. И конечно такая наука использует математику, как аппарат для расчетов. (Учитель демонстрирует карточки, портреты и другую наглядность по своему усмотрению, продолжает беседу).
5. Творческая работа. (10 мин)
Оборудование:Измерительный цилиндр (сосуд со шкалой) с водой и деревянный маленький брусок в форме параллелепипеда.
Выполнение работы:
1) Напомнить ученикам, что 1 миллилитр равен 1 кубическому сантиметру.
2) Объяснить коротко, что такое объем, найти объем параллелепипеда по формуле 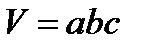 (объем параллелепипеда равен произведению трех его измерений, то есть длины, ширины и высоты).
(объем параллелепипеда равен произведению трех его измерений, то есть длины, ширины и высоты).
3) Измерить объем воды в измерительном цилиндре.
4) Опустить в сосуд с водой брусок.
5) Измерить теперь объем воды.
6) Вычислить объем вытесненной воды при погружении бруска.
7) Объем вытесненной воды должен совпасть с объемом бруска (1 мл=1 см3).
8) Сегодня на уроке ученики пятого класса открыли для себя закон Архимеда – один из законов физики.
9) Обозначив объем бруска - V3,объем воды в начале опыта - V1, объем воды с погруженным телом – V1, получим буквенное выражение V3=V2-V1.
Вывод: буквенные выражения - одно из средств, необходимое для определения законов физики.
6. Обобщение и систематизация знаний.
Остаток времени рекомендуем потратить на решение задач о движении, вспомнить понятие скорости, буквенное выражение, определяющую скорость и т.д. Можно выбрать задачи из учебника или из других источников. Тем самым напомнить еще раз, что физика изучает механические явления – явление движения.
Приложение 3
Задача 1.
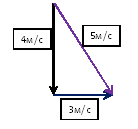 Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду. С какой скоростью он будет двигаться при горизонтальном ветре, скорость которого относительно Земли 3 м/с. На какое расстояние отнесет его от места падения, если он спускается с высоты 2 км?
Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду. С какой скоростью он будет двигаться при горизонтальном ветре, скорость которого относительно Земли 3 м/с. На какое расстояние отнесет его от места падения, если он спускается с высоты 2 км?
Решение:
1) Запишем закон сложения скоростей в векторном виде.
2) Сделаем чертеж, произведя сложение векторов скоростей.
3) Искомый вектор является гипотенузой прямоугольного треугольника. По теореме Пифагора вычислим её, найдя тем самым модуль скорости. 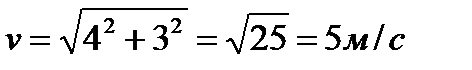
4) Зная, что при прямолинейном равномерном движении модуль перемещения пропорционален скорости, составим пропорцию и найдем модуль искомого перемещения.
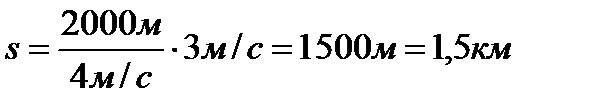
Следующие две задачи рекомендуем рассмотреть только после изучения тригонометрических функций острого угла.
Задача 2. Скорость лодки относительно течения 10 м/с, скорость течения 5 м/с. Под каким углом к береговой линии должен лодочник вести лодку, чтобы попасть на противоположный берег строго против того места, от которого он отплыл? Сделайте чертеж.
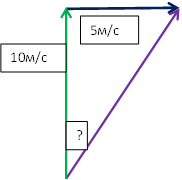 | Решение: 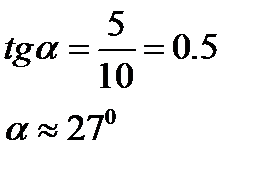 |
Задача 3. С какой силой F (эф) надо удерживать груз весом Р (пэ) на наклонной плоскости, чтобы он не сползал вниз?
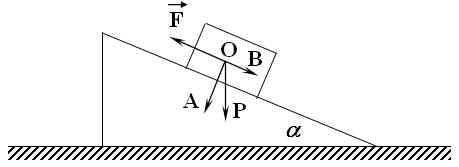
Решение: Пусть  – центр тяжести груза, к которому приложена сила
– центр тяжести груза, к которому приложена сила 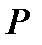 . Разложим вектор
. Разложим вектор 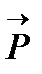 по двум взаимно перпендикулярным направлениям. Сила
по двум взаимно перпендикулярным направлениям. Сила 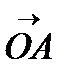 перпендикулярна наклонной плоскости и не вызывает перемещения груза. Сила
перпендикулярна наклонной плоскости и не вызывает перемещения груза. Сила 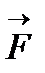 , удерживающая груз,
, удерживающая груз, 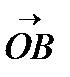 должна быть равной по величине и противоположной по направлению силе. Поэтому
должна быть равной по величине и противоположной по направлению силе. Поэтому 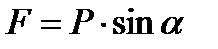 .
.
Задача4. Мяч брошен под углом 450 к горизонту со скоростью 20 м/с с поверхности Земли. Найдите высоту подъема мяча через 2 секунды.
Решение:
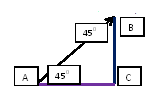
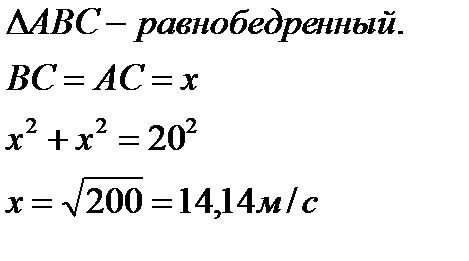
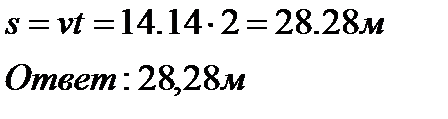
Теорема Пифагора
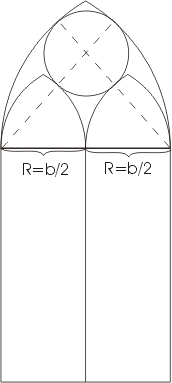 | При строительстве в зданиях готического и ромaнского стилей верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг и половине ширины (b/2), для внутренних дуг. Остается еще полная окружность, касающаяся четырех дуг. Так как она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра. |
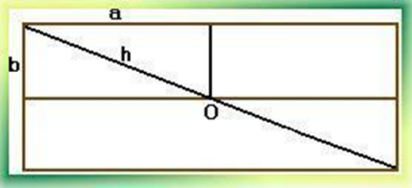 | Молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты. Задача: Определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту. Решение: По теореме Пифагора h2 ≥ a2+b2, значит h ≥ (a2+b2)½. |
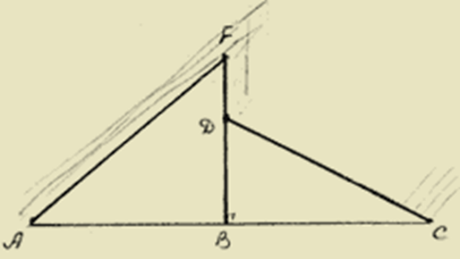 | При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки. Например, в доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки AC=8 м., и AB=BF. Решение: Треугольник ADC - равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда из треугольника DBC: DB=2,5 м., 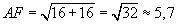 |
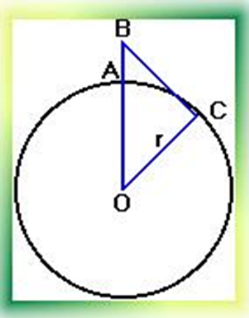 | В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например, в радиусе R=200 км, если известно, что радиус Земли равен 6380 км.) Решение: Пусть AB= x, BC=R=200 км, OC= r =6380 км. OB = OA + AB. OB = r + x. Используя теорему Пифагора, получим ответ. Ответ: 2,3 км. |
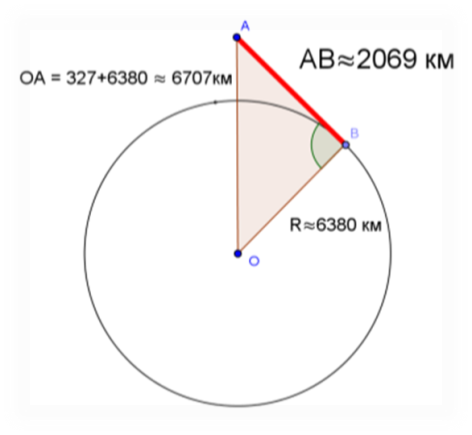 | 12 апреля 1961 года Ю.А. Гагарин на космическом корабле «Восток» был поднят над землёй на максимальную высоту 327 километров. На каком расстоянии от корабля находились в это время наиболее удалённые от него и видимые космонавтом участки поверхности Земли? (Радиус Земли ≈6400 км). Решение: Точка А – место расположения космического корабля. Точка В - видимый космонавтом участок поверхности Земли. Точка О – центр Земли. Так как АВ – касательная к окружности, а ОВ – радиус, то получаем, что треугольник АВО – прямоугольный с прямым углом В. ОВ=6380. ОА=327+6380=6707. По теореме Пифагора катет АВ=2069км. |
 | Задача из учебника «Арифметика» Леонтия Магницкого «Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти нужно.» Решение: По теореме Пифагора 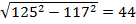 стоп. стоп. |
 | Задача из китайской «Математики в девяти книгах» Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша? Решение: x – глубина водоема, x+1 – длина камыша. По теореме Пифагора составим уравнение 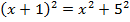 . Решив это уравнение, получаем значение x=12. Ответ: глубина озера составляет 12 метров, длина камыша – 13 метров. . Решив это уравнение, получаем значение x=12. Ответ: глубина озера составляет 12 метров, длина камыша – 13 метров. |
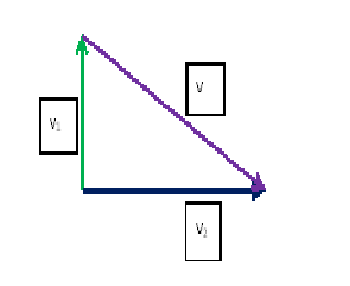 | 1) Задача: Какую скорость относительно воды должен сообщить мотор катеру, чтобы при скорости течения реки, равной 2 м/с, катер двигался перпендикулярно к берегу со скоростью 3,5 м/с относительно берега? Дано: 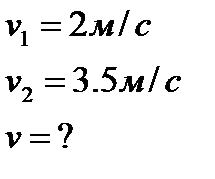 Решение: По теореме Пифагора получаем Решение: По теореме Пифагора получаем 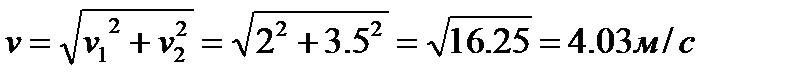 . . |
 | 1) Задача: Мяч брошен под углом 450 к горизонту со скоростью 20 м/с с поверхности Земли. Найдите высоту подъема мяча через 2 секунды. Решение: 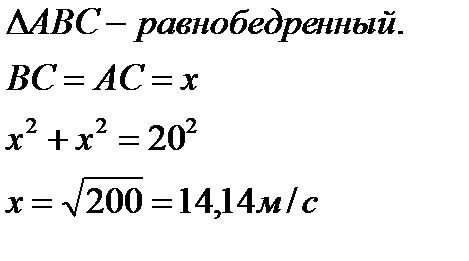 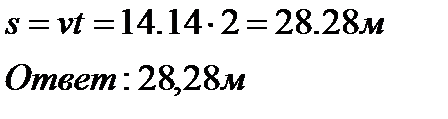 |
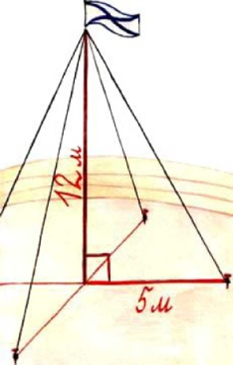 | 1) Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты? Решение: Длина троса является гипотенузой прямоугольного треугольника. По теореме Пифагора получаем 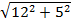 = = 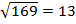 . Устанавливают 4 троса. . Устанавливают 4 троса. 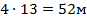 . Ответ: 50 метров троса не хватит, нужно еще 2 метра. . Ответ: 50 метров троса не хватит, нужно еще 2 метра. |
Приложение 4
Применение первоначальных сведений из теории чисел, теории групп и теории инвариантов как в математике, так и в физике.
На первых уроках по физике в 7 классе учитель обычно раскрывает смысл физический явлений, рассказывает о том, что физика – наука, которая изучает физические явления и процессы. Физика для исследования физических процессов использует математический аппарат исчисления. Нужно подвести детей к тому, что им придется изучить много формул, описывающие физические процессы. И здесь учителю необходимо раскрыть смысл записи больших и малых чисел в стандартном виде.
Так как дети еще с пятого класса по математике знают формулу 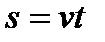 , то для постановки проблемного вопроса на уроке математике при изучении темы «стандартный вид числа» в 8 классе, можно дать задачу с большими величинами, решаемую с помощью этой формулы. Например:
, то для постановки проблемного вопроса на уроке математике при изучении темы «стандартный вид числа» в 8 классе, можно дать задачу с большими величинами, решаемую с помощью этой формулы. Например:
Задача: расстояние от Земли до солнца 150000000 км. За сколько секунд свет от Солнца дойдет до Земли, если скорость света 300000 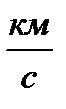 .
.
Решение: Воспользуемся известным определением: расстояние, прошедшее движущимся телом за единицу времени называется скоростью. Значит, нам нужно 150 миллионов километров поделить на 300 тысяч километров. 150 миллионов в стандартной записи имеет вид: 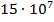 , то есть 150 000 000 =15
, то есть 150 000 000 =15  10 000 000=
10 000 000= 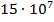 . Таким же образом запись 3 000 000 в стандартном виде будет таким:
. Таким же образом запись 3 000 000 в стандартном виде будет таким:  . Несколькими уроками ранее учащиеся изучили действия со степенями:
. Несколькими уроками ранее учащиеся изучили действия со степенями: 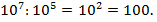 Итак, решение задачи:
Итак, решение задачи:
Дано: Решение:
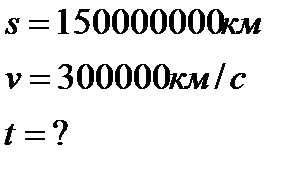
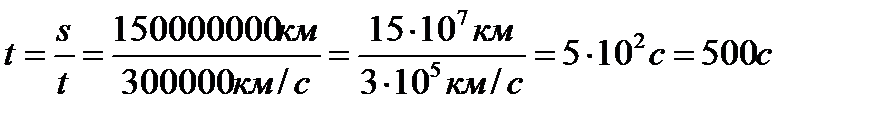
Если учитель хочет рассмотреть эту задачу на первых вводных уроках по физике, то ему придется объяснить детям тему «Действия со степенями», которую они будут изучать на уроках математики в 8 классе.
| При умножении степеней с одинаковыми основаниями показатели степени складываются. | 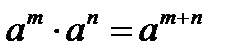 |
| При делении степеней с одинаковыми основаниями показатели степени вычитаются. | 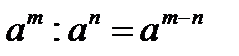 |
| При возведении степени в степень показатели степени перемножаются. | 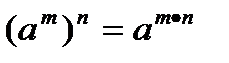 |
В восьмом классе по математике при изучении темы «Стандартный вид числа» предлагаем ввести названия больших малых чисел и сразу после введения определения «стандартный вид числа»:

| Количество нулей | ||
| миллион | 106 | |
| миллиард | 109 | |
| триллион | 1012 | |
| квадраллион | 1015 | |
| квинтиллион | 1018 | |
| Секстиллион | 1021 | |
| октиллион | 1027 | |
| нониллион | 1030 | |
| дециллион | 1033 |
Чтобы ввести понятие малых чисел, предлагаем решить следующую задачу.
Задача. Масса Земли приближенно равна 6 000 000 000 000 000 000 000 т, а масса атома водорода 0,0000000000000000000017 г. Во сколько раз Земля тяжелее атома водорода?
Дано:
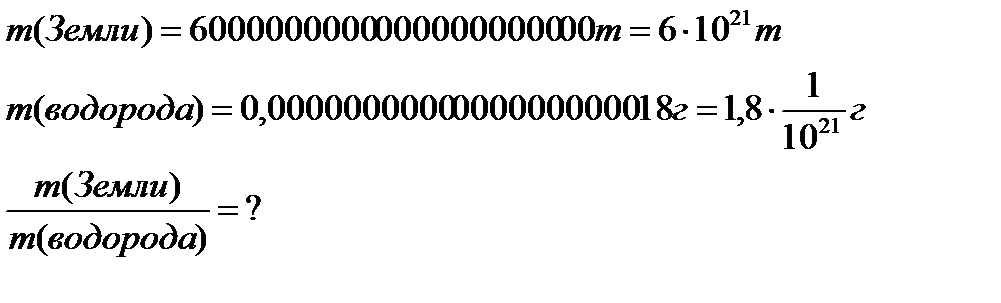
Решение:
Вначале ученикам нужно объяснить, что а в степени минус эн равен обратной величине а в степени э. Хотя по учебнику Макарычева Юрий Николаевича эта формулу рассматривают в 9 классе. А на уроках физики дети с ней сталкиваются, как только начинают решать серьезные задачи.
Итак, вводим формулу: 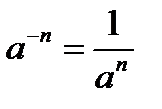 .
.
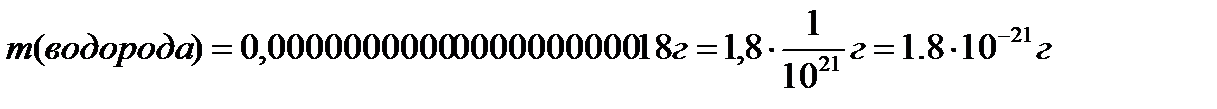 .
.
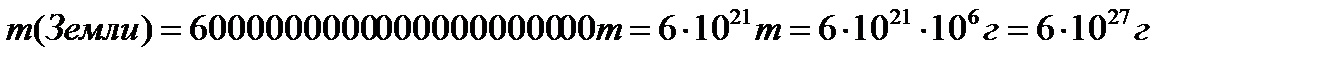 .
.
Вспомним, что при делении степеней с одинаковыми основаниями показатели степени вычитаются.
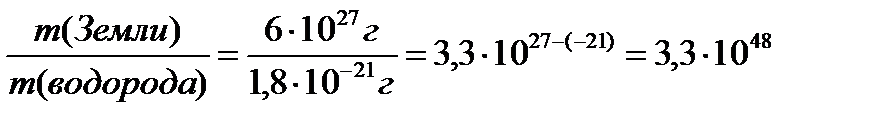
Даже на вводных уроках по физике бывает так, что учитель не обращает внимания на то, что дети не знают приставок СИ, что их надо запомнить, как таблицу умножения, «на века». Так хотя бы на уроках математики, при изучении темы «стандартное число» или «действия со степенями» необходимо эти приставки заучить наизусть.
| Приставка Обозначение | |||||
| Десятичный множитель | русская | международная | русское | международное | Пример |
| 101 | дека | deca | да | da | дал — декалитр |
| 102 | гекто | hecto | г | h | гПа — гектопаскаль |
| 103 | кило | kilo | к | k | кН — килоньютон |
| 106 | мега | Mega | М | M | МПа — мегапаскаль |
| 109 | гига | Giga | Г | G | ГГц — гигагерц |
| 1012 | тера | Tera | Т | T | ТВ — теравольт |
| 1015 | пета | Peta | П | P | Пфлопс — петафлопс |
| 1018 | экса | Peta | Э | E | ЭБ — эксабайт |
| 1021 | зетта | Exa | З | Z | ЗэВ — зеттаэлектронвольт |
| 1024 | йотта | Zetta | И | Y | ИБ — йоттабайт |
| Десятичный множитель | Приставка | Обозначение | |||
| русская | международная | русское | международное | Пример | |
| 10−1 | деци | deci | д | d | дм — дециметр |
| 10−2 | санти | centi | с | c | см — сантиметр |
| 10−3 | милли | milli | м | m | мH — миллиньютон |
| 10−6 | микро | micro | мк | µ (u) | мкм — микрометр, микрон |
| 10−9 | нано | nano | н | n | нм — нанометр |
| 10−12 | пико | pico | п | p | пФ — пикофарад |
| 10−15 | фемто | femto | ф | f | фс — фемтосекунда |
| 10−18 | атто | atto | а | a | ас — аттосекунда |
| 10−21 | зепто | zepto | з | z | зКл — зептокулон |
| 10−24 | йокто | yocto | и | y | иг — йоктограмм |
Предлагаем рассмотреть с учениками таблицу пересчета приставок дольных и кратных десятичных единиц физических величин.
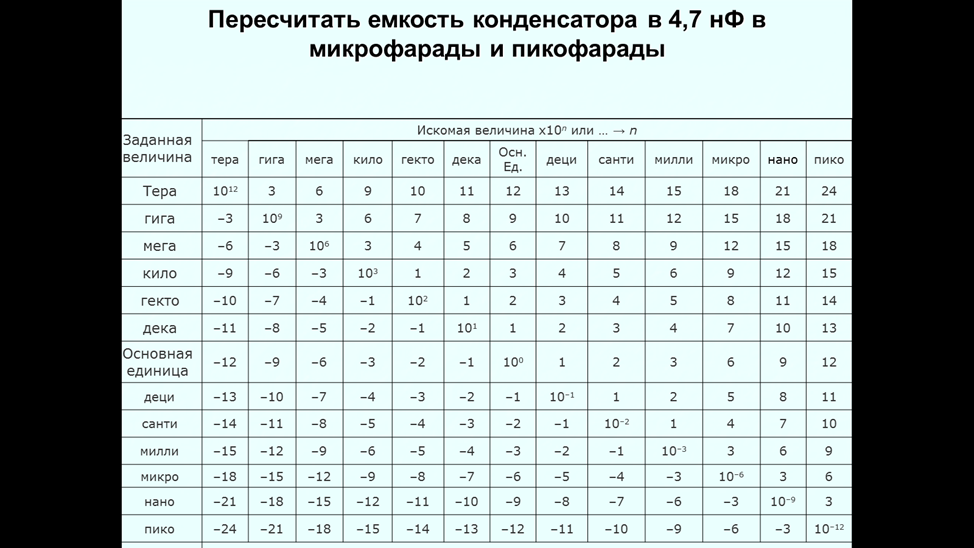
1) Для закрепления предлагаем следующую задачу.
Задача: Пересчитать длину волны 0,45 микрометров в метры и нанометры.
Решение: 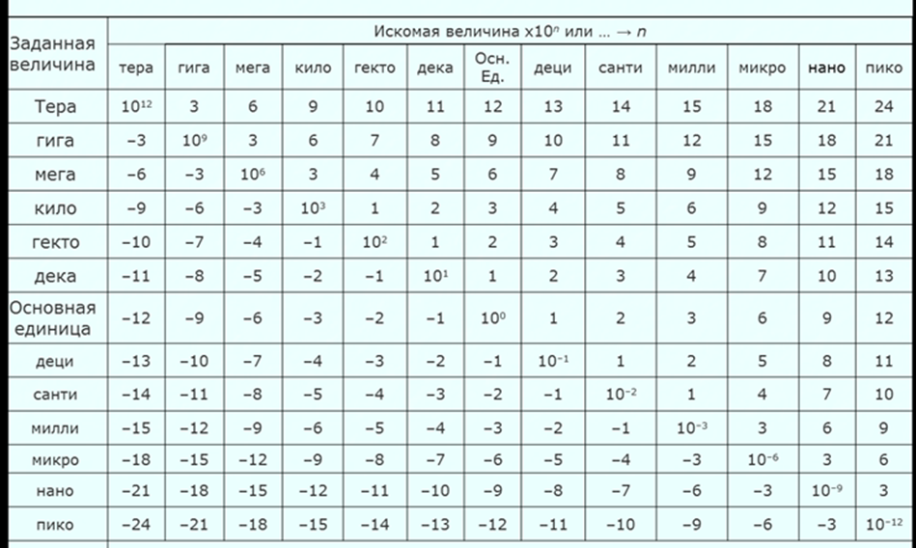
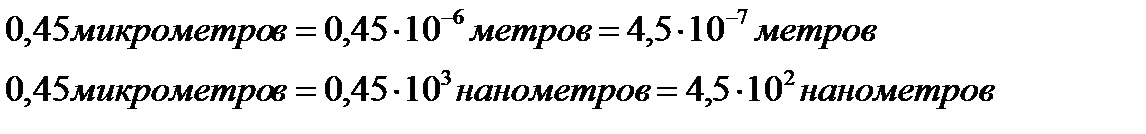
2) Основные сведения о планетах Солнечной системы – планетах земной группы.
