Системы обыкновенных дифференциальных уравнений
Система дифференциальных уравнений вида 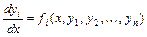
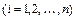 , где
, где 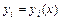 - искомые функции, называется нормальной системой дифференциальных уравнений. Число
- искомые функции, называется нормальной системой дифференциальных уравнений. Число  называется порядком системы. Совокупность
называется порядком системы. Совокупность  функций
функций 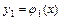 ,
, 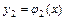 ,…,
,…, 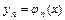 обращающих каждое уравнение системы в тождество, называется решением этой системы.
обращающих каждое уравнение системы в тождество, называется решением этой системы.
Условия 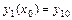 ,
, 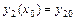 ,…,
,…, 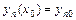 , где
, где 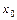 ,
, 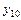 ,
, 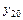 ,…,
,…, 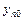 - заданные числа, называются начальными условиями. Задача нахождения решения нормальной системы уравнений, удовлетворяющего заданным начальным условиям, называется задачей Коши.
- заданные числа, называются начальными условиями. Задача нахождения решения нормальной системы уравнений, удовлетворяющего заданным начальным условиям, называется задачей Коши.
Общим решением нормальной системы ДУ называется решение:
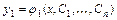 ,
, 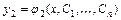 ,…,
,…, 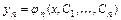 ,
,
зависящее от  произвольных постоянных
произвольных постоянных 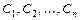 , такое, из которого при надлежащем выборе значений постоянных
, такое, из которого при надлежащем выборе значений постоянных 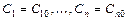 можно получить решение, удовлетворяющее заданным начальным условиям
можно получить решение, удовлетворяющее заданным начальным условиям 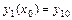 ,…,
,…, 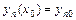 . Общее решение, заданное в неявном виде
. Общее решение, заданное в неявном виде 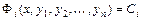 ,
, 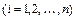 называется общим интегралом системы.
называется общим интегралом системы.
Частным решением системы называется решение 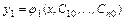 ,
, 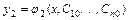 ,…,
,…, 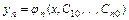 , получаемое из общего при конкретных значениях постоянных
, получаемое из общего при конкретных значениях постоянных 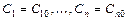 . Если для искомого частного решения системы заданы начальные условия
. Если для искомого частного решения системы заданы начальные условия 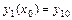 ,…,
,…, 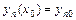 и известно общее решение
и известно общее решение 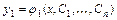 ,,…,
,,…, 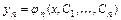 системы, то значения
системы, то значения 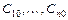 произвольных постоянных определяются, если это возможно, из системы уравнений
произвольных постоянных определяются, если это возможно, из системы уравнений 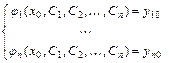 .
.
Нормальные системы ДУ с небольшим числом уравнений решают методом исключения неизвестных функций приводя их к одному дифференциальному уравнению  -го порядка или к нескольким уравнениям порядка, меньшего чем
-го порядка или к нескольким уравнениям порядка, меньшего чем  .
.
Для нахождения решения, например, нормальной системы двух уравнений 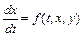 ,
, 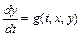 , где
, где 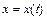 ,
, 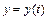 - неизвестные функции независимой переменной
- неизвестные функции независимой переменной 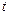 поступают следующим образом. Сначала дифференцируют по
поступают следующим образом. Сначала дифференцируют по 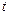 первое из уравнений системы и получают уравнение
первое из уравнений системы и получают уравнение 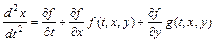 . Затем определяют
. Затем определяют 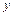 из первого уравнения системы и подставляют найденное выражение
из первого уравнения системы и подставляют найденное выражение 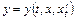 в уравнение
в уравнение 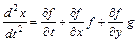 . В результате получают ДУ второго порядка относительно неизвестной функции
. В результате получают ДУ второго порядка относительно неизвестной функции 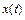 , решая которое находят
, решая которое находят 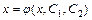 , где
, где 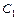 и
и 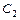 -произвольные постоянные. Подставляя
-произвольные постоянные. Подставляя 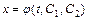 в формулу
в формулу 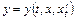 , определяют функцию
, определяют функцию 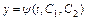 . Совокупность функций
. Совокупность функций 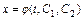 ,
, 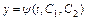 даёт общее решение системы.
даёт общее решение системы.
Однородной линейной системой  уравнений с постоянными коэффициентами называется система вида
уравнений с постоянными коэффициентами называется система вида 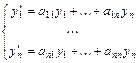 или, в матрично-векторной записи
или, в матрично-векторной записи 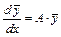 , где
, где 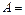
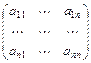 - матрица системы,
- матрица системы, 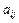 - постоянные коэффициенты,
- постоянные коэффициенты, 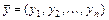 - вектор неизвестных функций
- вектор неизвестных функций 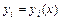 .
.
Для построения общего решения однородной линейной системы достаточно знать  линейно независимых частных решений:
линейно независимых частных решений:
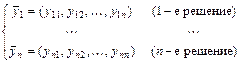 .
.
Такая система решений называется фундаментальной.
Если известна фундаментальная система решений (ФСР), то их линейная комбинация 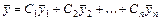 , где
, где 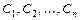 - произвольные постоянные, представляет собой общее решение однородной линейной системы дифференциальных уравнений.
- произвольные постоянные, представляет собой общее решение однородной линейной системы дифференциальных уравнений.
Основным методом построения фундаментальной системы решений является метод Эйлера. Согласно этому методу частное решение системы ищут в виде 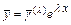 , где
, где 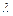 -собственное число матрицы
-собственное число матрицы 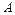 , определяемое как корень характеристического уравнения
, определяемое как корень характеристического уравнения 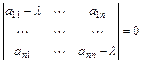 ;
; 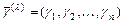 - какой-нибудь собственный вектор этой матрицы, соответствующий числу
- какой-нибудь собственный вектор этой матрицы, соответствующий числу 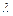 и определяемый как ненулевое решение системы линейных алгебраических уравнений
и определяемый как ненулевое решение системы линейных алгебраических уравнений 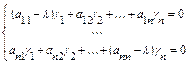 .
.
Каждому из собственных чисел матрицы 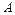 , являющихся корнями характеристического уравнения, соответствует хотя бы одно частное решение указанного вида, при этом возможны следующие случаи:
, являющихся корнями характеристического уравнения, соответствует хотя бы одно частное решение указанного вида, при этом возможны следующие случаи:
1) Если 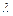 - действительный простой корень характеристического уравнения, то ему в ФСР соответствует одно частное решение
- действительный простой корень характеристического уравнения, то ему в ФСР соответствует одно частное решение 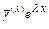 , где
, где 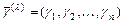 - какой-нибудь собственный вектор матрицы
- какой-нибудь собственный вектор матрицы 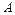 , соответствующий числу
, соответствующий числу 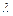 .
.
2)Если 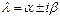 - пара комплексно-сопряжённых простых корней характеристического уравнения, то ей в ФСР соответствует два линейно независимых частных решения
- пара комплексно-сопряжённых простых корней характеристического уравнения, то ей в ФСР соответствует два линейно независимых частных решения 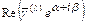 ,
, 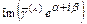 , где
, где 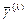 - комплексный собственный вектор матрицы
- комплексный собственный вектор матрицы 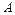 , соответствующий комплексному собственному числу
, соответствующий комплексному собственному числу 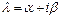 .
.
3) Если 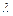 - действительный корень кратности
- действительный корень кратности 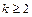 характеристического уравнения, то соответствующее ему решение, содержащее
характеристического уравнения, то соответствующее ему решение, содержащее 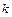 произвольных постоянных
произвольных постоянных 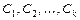 и входящее в общее решение исходной системы, ищется в виде произведения векторного многочлена степени
и входящее в общее решение исходной системы, ищется в виде произведения векторного многочлена степени 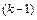 на
на 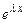 :
: 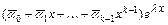 . Чтобы найти векторные коэффициенты
. Чтобы найти векторные коэффициенты 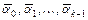 , надо подставить данное решение в систему
, надо подставить данное решение в систему 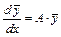 . Приравняв коэффициенты подобных членов в левой и правой частях уравнений системы, получим систему линейных алгебраических уравнений для определения неизвестных координат векторов
. Приравняв коэффициенты подобных членов в левой и правой частях уравнений системы, получим систему линейных алгебраических уравнений для определения неизвестных координат векторов 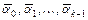 , причём среди координат этих векторов
, причём среди координат этих векторов 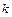 координат являются произвольными и полагаются равными
координат являются произвольными и полагаются равными 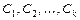 , а остальные выражаются через них.
, а остальные выражаются через них.
В задачах 9.245-9.252найти методом исключения общие решения однородных систем дифференциальных уравнений:
9.245 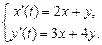 9.246
9.246 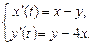
9.247 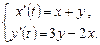 9.248
9.248 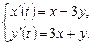
9.249 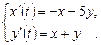 9.250
9.250 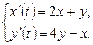
9.251 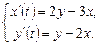 9.252
9.252 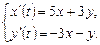
В задачах 9.253-9.258 найти общие решения следующих однородных систем уравнений (для облегчения работы в задачах указаны корни характеристического уравнения):
9.253 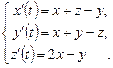 9.254
9.254 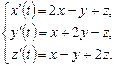
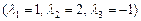
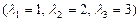
9.255 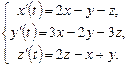 9.256
9.256 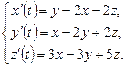
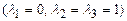
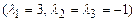
9.257 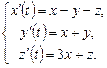 9.258
9.258 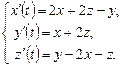
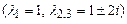
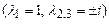
В задачах 9.259-9.262 найти методом исключения общие решения следующих неоднородных систем уравнений:
9.259 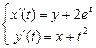 . 9.260
. 9.260 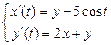 .
.
9.261 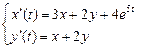 . 9.262
. 9.262 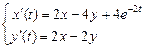 .
.
Решение 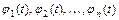 нормальной системы ДУ
нормальной системы ДУ 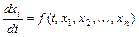 ,
, 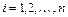 , определённое при всех
, определённое при всех 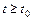 называется устойчивым по Ляпунову, если для любого
называется устойчивым по Ляпунову, если для любого 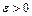 существует
существует 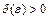 такое, что для всякого решения
такое, что для всякого решения 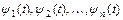 той же системы, значения которого в точке
той же системы, значения которого в точке 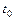 удовлетворяют неравенствам
удовлетворяют неравенствам 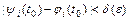 ,
, 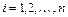 , при всех
, при всех 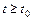 справедливы неравенства
справедливы неравенства 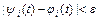 ,
, 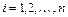 . Если решение
. Если решение 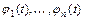 не только устойчиво, но и при условии
не только устойчиво, но и при условии 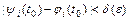 ,
, 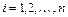 , удовлетворяет соотношению
, удовлетворяет соотношению 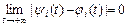 ,
, 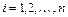 , то это решение называется асимптотически устойчивым.
, то это решение называется асимптотически устойчивым.
Если система дифференциальных уравнений описывает некоторое движение, то в случае устойчивости решений характер движений мало изменяется при малом изменении начальных данных.
Вопрос об устойчивости решения 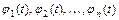 системы
системы 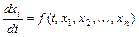 ,
, 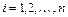 , сводится к вопросу об устойчивости нулевого решения (точки покоя) другой системы, получаемой из данной с помощью замены
, сводится к вопросу об устойчивости нулевого решения (точки покоя) другой системы, получаемой из данной с помощью замены 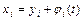 ,
, 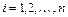 .
.
Точкой покоя системы 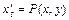 ,
, 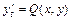 , где функции
, где функции 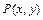 ,
, 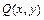 - непрерывно дифференцируемы, называется такая точка, в которой
- непрерывно дифференцируемы, называется такая точка, в которой 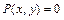 и
и 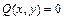 .
.
Точкой покоя системы двух однородных ЛДУ с постоянными коэффициентами 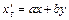 ,
, 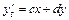 ,
, 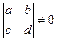 является начало координат
является начало координат 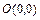 , т.е. нулевое решение данной системы. Для исследования точки покоя такой системы, надо найти корни
, т.е. нулевое решение данной системы. Для исследования точки покоя такой системы, надо найти корни 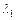 и
и 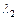 характеристического уравнения системы
характеристического уравнения системы 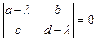 и в зависимости от вида корней, определить характер точки покоя, в соответствие с приведённой в таблице их классификацией.
и в зависимости от вида корней, определить характер точки покоя, в соответствие с приведённой в таблице их классификацией.
Корни 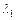 , , 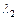 | Характер точки покоя | Устойчивость точки покоя | |
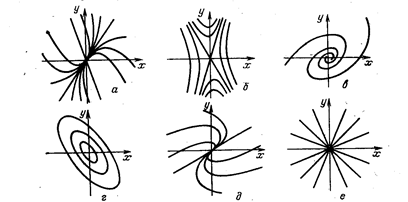
Действительные и различные: 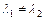 | 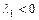 , , 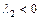 | Устойчивый узел (рис. a) | Асимптотически устойчива |
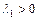 , , 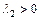 | Неустойчивый узел (рис. a) | Неустойчива | |
| Разных знаков | Седло (рис. б) | Неустойчива | |
Комплексно-сопряжённые: 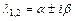 | 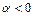 , , 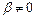 | Устойчивый фокус (рис. в) | Асимптотически устойчива |
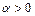 , , 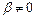 | Неустойчивый фокус (рис. в) | Неустойчива | |
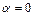 , , 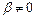 | Центр (рис.г) | Устойчива | |
Действительные и равные 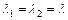 | 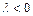 | Устойчивый вырожденный узел (рис. д) | Асимптотически устойчива |
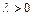 | Неустойчивый вырожденный узел (рис. д) | Неустойчива | |
Действительные и равные 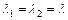 (для системы (для системы 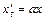 , , 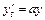 ) ) | 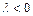 | Устойчивый дикритический узел (рис. е) | Асимптотически устойчива |
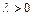 | Неустойчивый дикритический узел (рис. е) | Неустойчива |
Если система 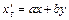 ,
, 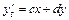 описывает движение точки
описывает движение точки 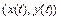 , то интегральные кривые называют траекториями движения точки. В случае устойчивого узла и фокуса точка
, то интегральные кривые называют траекториями движения точки. В случае устойчивого узла и фокуса точка 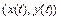 , двигаясь по траекториям, неограниченно приближается к началу координат при
, двигаясь по траекториям, неограниченно приближается к началу координат при 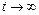 , и неограниченно удаляется от него в противном случае.
, и неограниченно удаляется от него в противном случае.
В задачах 9.263-9.272определить характер точек покоя следующих систем дифференциальных уравнений.
9.263 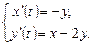 9.264
9.264 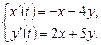
9.265 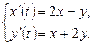 9.266
9.266 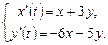
9.267 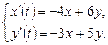 9.268
9.268 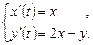
9.269 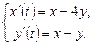 9.270
9.270 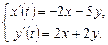
9.271 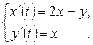 9.272
9.272 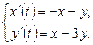
Однородная линейная система уравнений с постоянными коэффициентами 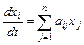 ,
, 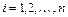 , где
, где 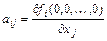 называется системой уравнений первого приближения для системы
называется системой уравнений первого приближения для системы 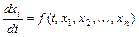 ,
, 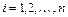 . При этом справедливо следующее утверждение: если все корни характеристического уравнения системы первого приближения имеют отрицательные действительные части, то её точка покоя, а также исходной системы асимптотически устойчива; если хотя бы один из корней характеристического уравнения системы первого приближения имеет положительную действительную часть, то её точка покоя, а также исходной системы неустойчива. Если же среди корней характеристического уравнения имеется хотя бы одно с нулевой действительной частью, а остальные – с отрицательной, то в этом случае исследование на устойчивость по первому приближению невозможно, так как начинает сказываться влияние членов второго порядка малости относительно
. При этом справедливо следующее утверждение: если все корни характеристического уравнения системы первого приближения имеют отрицательные действительные части, то её точка покоя, а также исходной системы асимптотически устойчива; если хотя бы один из корней характеристического уравнения системы первого приближения имеет положительную действительную часть, то её точка покоя, а также исходной системы неустойчива. Если же среди корней характеристического уравнения имеется хотя бы одно с нулевой действительной частью, а остальные – с отрицательной, то в этом случае исследование на устойчивость по первому приближению невозможно, так как начинает сказываться влияние членов второго порядка малости относительно 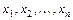 .
.
В задачах 9.273-9.278исследовать на устойчивость по первому приближению нулевое решение следующих систем:
9.273 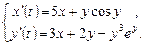 9.274
9.274 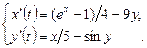
9.275 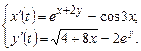 9.276
9.276 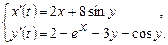
9.277 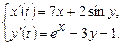 9.278
9.278 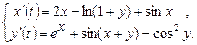
В задачах 9.279-9.280исследовать, при каких значениях параметра 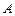 асимптотически устойчиво нулевое решение:
асимптотически устойчиво нулевое решение:
9.279 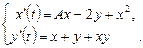 9.280
9.280 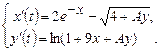
Разностные уравнения.
Если неизвестная функция 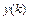 и заданная функция
и заданная функция 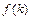 являются функциями одного целочисленного аргумента
являются функциями одного целочисленного аргумента 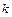 , то уравнение вида
, то уравнение вида 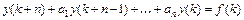 ,
, 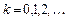 , где
, где 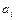
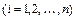 - постоянные коэффициенты, называется линейным разностным уравнением (ЛРУ)
- постоянные коэффициенты, называется линейным разностным уравнением (ЛРУ) 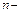 го порядка с постоянными коэффициентами. Если
го порядка с постоянными коэффициентами. Если 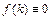 , то уравнение называется однородным.
, то уравнение называется однородным.
Функция 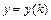 ,
, 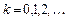 , обращающая разностное уравнение в тождество, называется его решением.
, обращающая разностное уравнение в тождество, называется его решением.
Условия 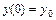 ,
, 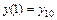 ,…,
,…, 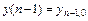 , где
, где 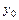 ,
, 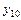 ,…,
,…, 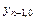 - заданные числа, называются начальными условиями.
- заданные числа, называются начальными условиями.
Общим решением РУ  -го порядка называется решение
-го порядка называется решение 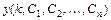 , зависящее от
, зависящее от  произвольных постоянных
произвольных постоянных 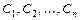 , такое, из которого при надлежащем выборе значений постоянных
, такое, из которого при надлежащем выборе значений постоянных 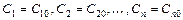 можно получить решение
можно получить решение 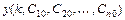 , удовлетворяющее заданным начальным условиям
, удовлетворяющее заданным начальным условиям 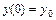 ,
, 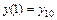 ,…,
,…, 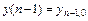 . Частным решением называется решение
. Частным решением называется решение 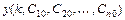 , получаемое из общего при конкретных значениях постоянных
, получаемое из общего при конкретных значениях постоянных 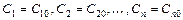 .
.
Общее решение однородного ЛРУ  -го порядка
-го порядка 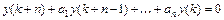 ищется, аналогично общему решению дифференциального уравнения
ищется, аналогично общему решению дифференциального уравнения 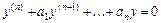 , в виде
, в виде 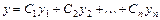 , где
, где 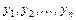 - фундаментальная система его решений;
- фундаментальная система его решений; 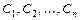 - произвольные постоянные.
- произвольные постоянные.
Фундаментальной системой решений однородного ЛРУ  -го порядка
-го порядка 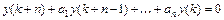 называется любая система из
называется любая система из  линейно независимых частных решений
линейно независимых частных решений 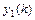 ,
, 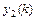 ,…,
,…, 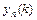 этого уравнения.
этого уравнения.
Фундаментальная система решений 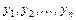 строится на основе характера корней характеристического уравнения
строится на основе характера корней характеристического уравнения 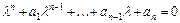 . А именно: 1) если
. А именно: 1) если 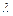 - действительный простой корень характеристического уравнения, то ему в ФСР соответствует частное решение
- действительный простой корень характеристического уравнения, то ему в ФСР соответствует частное решение 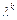 разностного уравнения; 2)если
разностного уравнения; 2)если 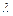 - действительный корень кратности
- действительный корень кратности 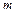 , то ему в ФСР соответствует
, то ему в ФСР соответствует 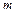 линейно независимых частных решений:
линейно независимых частных решений: 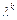 ,
, 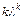 ,
, 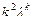 ,…,
,…, 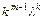 ; 3) если
; 3) если 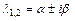 - пара простых комплексно-сопряжённых корней характеристического уравнения, то ей в ФСР соответствует два линейно независимых частных решения:
- пара простых комплексно-сопряжённых корней характеристического уравнения, то ей в ФСР соответствует два линейно независимых частных решения: 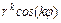 ,
, 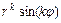 , где
, где 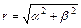 ,
, 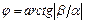 .
.
Общее решение неоднородного линейного разностного уравнения 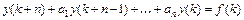 имеет вид
имеет вид 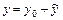 , где
, где 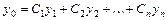 - общее решение соответствующего однородного разностного уравнения,
- общее решение соответствующего однородного разностного уравнения, 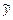 - какое-нибудь частное решение данного неоднородного уравнения.
- какое-нибудь частное решение данного неоднородного уравнения.
Как и в случае дифференциальных уравнений, частное решение 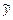 разностного уравнения с правой частью специального вида
разностного уравнения с правой частью специального вида 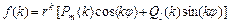 ищется методом неопределённых коэффициентов в виде
ищется методом неопределённых коэффициентов в виде 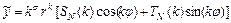 , где
, где 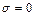 , если число
, если число 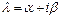 , для которого
, для которого 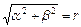 и
и 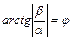 , не является корнем характеристического уравнения, и
, не является корнем характеристического уравнения, и 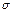 равно кратности корня
равно кратности корня 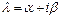 в противном случае;
в противном случае; 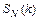 и
и 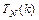 - полные многочлены степени
- полные многочлены степени 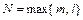 с неопределёнными коэффициентами. Примерами полных многочленов с неопределёнными коэффициентами степени
с неопределёнными коэффициентами. Примерами полных многочленов с неопределёнными коэффициентами степени 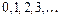 соответственно являются:
соответственно являются: 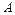 ,
, 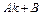 ,
, 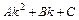 ,
, 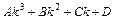 ,…. Для нахождения коэффициентов многочленов
,…. Для нахождения коэффициентов многочленов 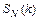 и
и 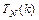 , надо подставить решение
, надо подставить решение 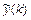 в неоднородное разностное уравнение и приравнять коэффициенты при подобных членах в левой и правой частях полученного равенства. В результате получим систему уравнений, решив которую, найдём значения коэффициентов.
в неоднородное разностное уравнение и приравнять коэффициенты при подобных членах в левой и правой частях полученного равенства. В результате получим систему уравнений, решив которую, найдём значения коэффициентов.
В задачах 9.281-9.288 найти общие решения следующих однородных разностных уравнений:
9.281 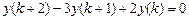 .
.
9.282 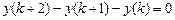 .
.
9.283 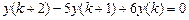 .
.
9.284 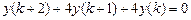 .
.
9.285 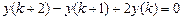 .
.
9.286 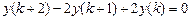 .
.
9.287 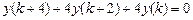 .
.
9.288 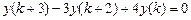 .
.
В задачах 9.289-9.292 найти частные решения разностных уравнений, удовлетворяющие указанным начальным условиям:
9.289 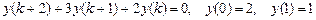 .
.
9.290 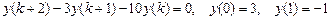 .
.
9.291 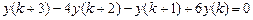 ,
,
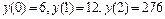 .
.
9.292 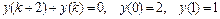 .
.
В задачах 9.293-9.308 найти общие решения следующих неоднородных разностных уравнений
9.293 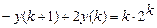 .
.
9.294 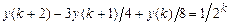 .
.
9.295 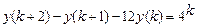 .
.
9.296 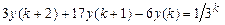 .
.
9.297 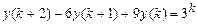 .
.
9.298 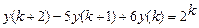 .
.
9.299 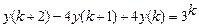 .
.
9.300 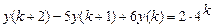 .
.
9.301 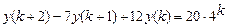 .
.
9.302 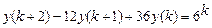 .
.
9.303 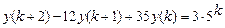 .
.
9.304 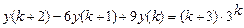 .
.
9.305  .
.
9.306 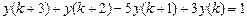 .
.
9.307 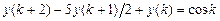 .
.
9.308 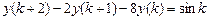 .
.
В задачах 9.309-9.312 найти частные решения разностных уравнений, удовлетворяющие указанным начальным условиям:
9.309 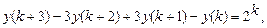
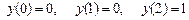 .
.
9.310 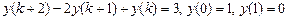 .
.
9.311 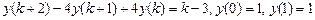 .
.
9.312 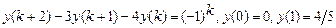 .
.
По аналогии с нормальными системами дифференциальных уравнений рассматриваются также и нормальные системы разностных уравнений вида 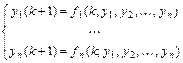 , где
, где  - искомые функции,
- искомые функции, 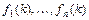 - заданные функции целочисленного аргумента
- заданные функции целочисленного аргумента 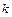 ,
, 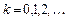 . Число
. Число  называется порядком системы. Совокупность
называется порядком системы. Совокупность  функций
функций 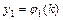 ,
, 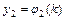 ,…,
,…, 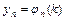 обращающих каждое уравнение системы в тождество, называется решением этой системы.
обращающих каждое уравнение системы в тождество, называется решением этой системы.
Условия 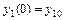 ,
, 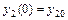 ,…,
,…, 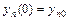 , где
, где 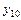 ,
, 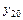 ,…,
,…, 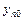 - заданные числа, называются начальными условиями.
- заданные числа, называются начальными условиями.
Общим решением системы РУ  -го порядка называется решение:
-го порядка называется решение:
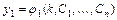 ,
, 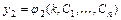 ,…,
,…, 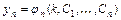 ,
,
зависящее от  произвольных постоянных
произвольных постоянных 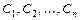 , такое, из которого при надлежащем выборе значений постоянных
, такое, из которого при надлежащем выборе значений постоянных 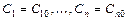 можно получить решение, удовлетворяющее заданным начальным условиям
можно получить решение, удовлетворяющее заданным начальным условиям 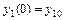 ,
, 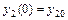 ,…,
,…, 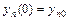 .
.
Частным решением системы называется решение 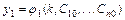 ,
, 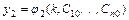 ,…,
,…, 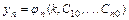 , получаемое из общего при конкретных значениях постоянных
, получаемое из общего при конкретных значениях постоянных 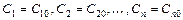 .
.
Нормальные системы разностных уравнений аналогично системам дифференциальных уравнений можно решать методом исключения неизвестных функций приводя их к одному разностному уравнению  -го порядка. Для нахождения решения, например, системы двух разностных уравнений
-го порядка. Для нахождения решения, например, системы двух разностных уравнений 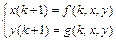 , где
, где 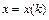 ,
, 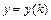 - неизвестные функции целочисленного аргумента
- неизвестные функции целочисленного аргумента 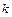 поступают следующим образом. Сначала, используя первое из уравнений системы, получим уравнение
поступают следующим образом. Сначала, используя первое из уравнений системы, получим уравнение 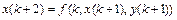 , в которое затем подставим второе уравнение системы
, в которое затем подставим второе уравнение системы 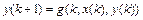 , с учётом выражения
, с учётом выражения 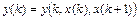 , найденного из первого уравнения системы. В результате получим разностное уравнение 2-го порядка относительно неизвестной функции
, найденного из первого уравнения системы. В результате получим разностное уравнение 2-го порядка относительно неизвестной функции 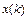 , решив которое найдём функцию
, решив которое найдём функцию 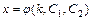 , где
, где 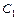 ,
, 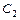 - произвольные постоянные. Подставив
- произвольные постоянные. Подставив 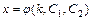 в формулу
в формулу 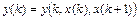 , определим функцию
, определим функцию 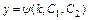 . Совокупность функций
. Совокупность функций 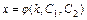 ,
, 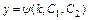 даёт общее решение системы.
даёт общее решение системы.
В задачах 9.313-9.320найти методом исключения решения следующих систем разностных уравнений:
9.313 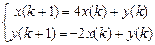 . 9.314
. 9.314 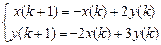 .
.
9.315 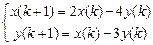 . 9.316
. 9.316 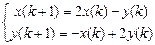 .
.
9.317 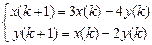 . 9.318
. 9.318 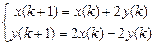 .
.
9.319 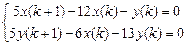 .
.
9.320 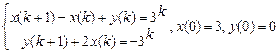 .
.
