Выпуклость и вогнутость кривой. Точки её перегиба. Достаточные признаки выпуклости, вогнутости и точек перегиба кривой
Кривая 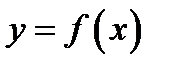 называется выпуклой в интервале
называется выпуклой в интервале 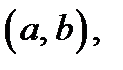 если она лежит ниже любой своей касательной в точках, абсциссы которых лежат в этом интервале (см. рис. 68).
если она лежит ниже любой своей касательной в точках, абсциссы которых лежат в этом интервале (см. рис. 68).


 Кривая
Кривая 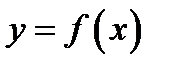 называется вогнутой в интервале
называется вогнутой в интервале 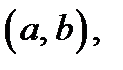 если она лежит выше любой своей касательной в точках, абсциссы которых лежат в этом интервале(см. рис. 69).
если она лежит выше любой своей касательной в точках, абсциссы которых лежат в этом интервале(см. рис. 69).
Точка кривой, отделяющая выпуклую часть от вогнутой, называется точкой перегиба. Ясно, что касательная к кривой в точке перегиба пересекает кривую, т. к. выпуклая часть лежит ниже касательной, а вогнутая – выше касательной (см. рис. 70).
Здесь и далее будем считать, что функция 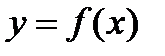 дважды дифференцируема всюду в области определения.
дважды дифференцируема всюду в области определения.
Известно, что вычисленная в точке 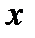 производная
производная 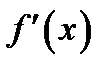 равна тангенсу угла
равна тангенсу угла 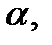 образованного с осью
образованного с осью 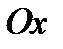 касательной к кривой в её точке с абсциссой
касательной к кривой в её точке с абсциссой 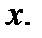 Для выпуклой кривой (см. рис. 68) с увеличением
Для выпуклой кривой (см. рис. 68) с увеличением 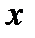 угол
угол 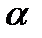 убывает, следовательно, убывает
убывает, следовательно, убывает 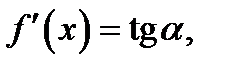 значит, производная
значит, производная 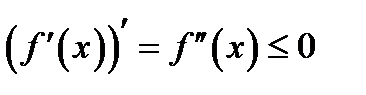 согласно необходимому признаку убывания функции. Аналогично убедимся в том, что если кривая
согласно необходимому признаку убывания функции. Аналогично убедимся в том, что если кривая 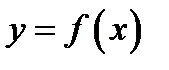 вогнутая, то
вогнутая, то 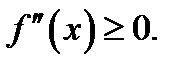 Итак, пришли к теореме.
Итак, пришли к теореме.
Теорема 6 (необходимые признаки выпуклости и вогнутости кривой). Если кривая 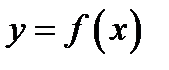 является выпуклой на
является выпуклой на 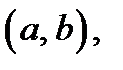 то в этом интервале
то в этом интервале 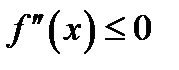 ; если кривая
; если кривая 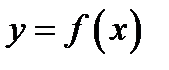 является вогнутой на
является вогнутой на 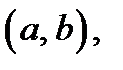 то в этом интервале
то в этом интервале 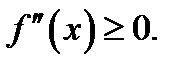
Теорема 7 (достаточные признаки выпуклости и вогнутости кривой). Если 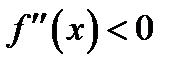 всюду в интервале
всюду в интервале 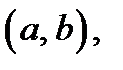 то в этом интервале кривая
то в этом интервале кривая 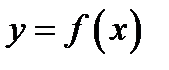 выпуклая. Если
выпуклая. Если 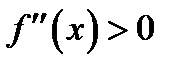 всюду в интервале
всюду в интервале 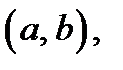 то в этом интервале кривая
то в этом интервале кривая 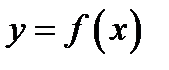 вогнутая.
вогнутая.
Доказательство. Докажем первую часть теоремы. Пусть 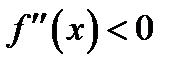 всюду в интервале
всюду в интервале 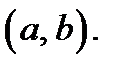 Тогда, согласно достаточному признаку убывания функции, в этом интервале
Тогда, согласно достаточному признаку убывания функции, в этом интервале 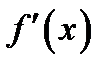 убывает с увеличением
убывает с увеличением 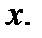 Значит,
Значит, 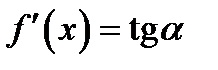 убывает всюду в интервале
убывает всюду в интервале 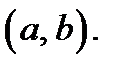 Следовательно, кривая
Следовательно, кривая 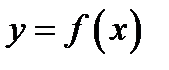 является выпуклой, что очевидно геометрически. Теорема доказана.
является выпуклой, что очевидно геометрически. Теорема доказана.
Теорема 8 (необходимый признак точки перегиба). Если 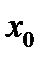 – абсцисса точки перегиба кривой
– абсцисса точки перегиба кривой 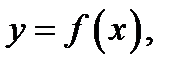 то
то 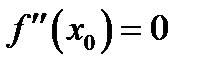 или не существует.
или не существует.
Доказательство.Точка перегиба отделяет выпуклую часть от вогнутой, следовательно, она одновременно принадлежит обеим указанным частям кривой. Будем считать, что вторая производная 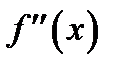 существует и непрерывна в точке
существует и непрерывна в точке 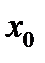 . Для выпуклой части кривой
. Для выпуклой части кривой 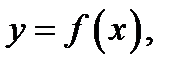 согласно необходимому признаку выпуклости кривой,
согласно необходимому признаку выпуклости кривой, 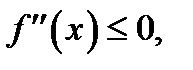 поэтому
поэтому 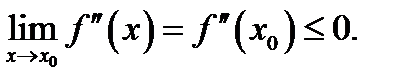 Для вогнутой части кривой
Для вогнутой части кривой 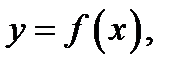 согласно необходимому признаку вогнутости кривой,
согласно необходимому признаку вогнутости кривой, 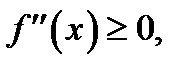 поэтому
поэтому 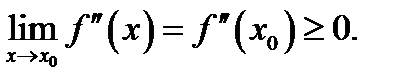 Но эти два соотношения должны выполняться одновременно, следовательно,
Но эти два соотношения должны выполняться одновременно, следовательно, 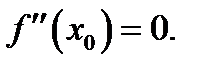 Теорема доказана.
Теорема доказана.
Абсциссой точки перегиба может служить и значение 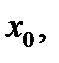 при котором
при котором 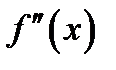 не существует. Покажем это на примере кривой
не существует. Покажем это на примере кривой 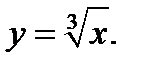 Здесь
Здесь 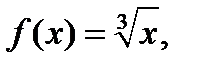
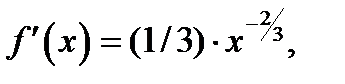
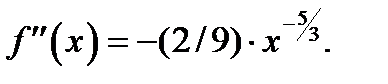 Отметим, что при
Отметим, что при 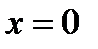 вторая производная
вторая производная 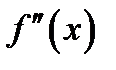 не существует, т. е. не существует
не существует, т. е. не существует 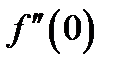 . Кроме того, видим, что
. Кроме того, видим, что 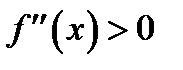 при
при 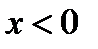 , а при
, а при 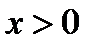 имеем
имеем 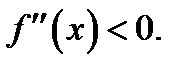 Значит, по теореме 7 при
Значит, по теореме 7 при 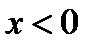 кривая вогнутая, при
кривая вогнутая, при 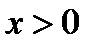 - выпуклая. Это означает, что
- выпуклая. Это означает, что 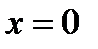 есть абсцисса точки перегиба рассматриваемой кривой. Это также очевидно из графика функции (см. рис. 71).
есть абсцисса точки перегиба рассматриваемой кривой. Это также очевидно из графика функции (см. рис. 71).
Теорема 9 (достаточный признак точки перегиба). Точка 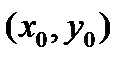 кривой
кривой 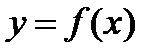 является точкой перегиба, если
является точкой перегиба, если 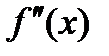 обращается в нуль или не существует при
обращается в нуль или не существует при 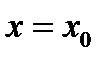 и знак второй производной
и знак второй производной 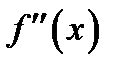 изменяется при переходе
изменяется при переходе 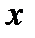 через
через 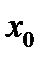 (с увеличением
(с увеличением 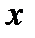 ). При перемене знака с «‑» на «+» участок выпуклости сменяется участком вогнутости, а при перемене с «+» на «‑» участок вогнутости сменяется участком выпуклости.
). При перемене знака с «‑» на «+» участок выпуклости сменяется участком вогнутости, а при перемене с «+» на «‑» участок вогнутости сменяется участком выпуклости.
Доказательство.Пусть знак 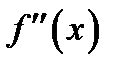 изменяется с «‑» на «+» при переходе
изменяется с «‑» на «+» при переходе 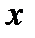 через
через 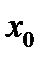 с увеличением
с увеличением 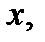 т. е. при
т. е. при 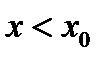 имеем
имеем 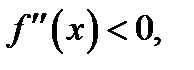 а при
а при 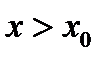 получим
получим 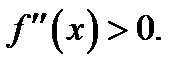 Тогда, согласно достаточному признаку выпуклости и вогнутости кривой, слева от
Тогда, согласно достаточному признаку выпуклости и вогнутости кривой, слева от 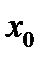 лежит участок выпуклости кривой, а справа от
лежит участок выпуклости кривой, а справа от 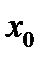 – участок вогнутости. Следовательно,
– участок вогнутости. Следовательно, 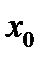 – абсцисса точки перегиба кривой
– абсцисса точки перегиба кривой 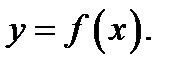 Вторая часть теоремы доказывается аналогично.
Вторая часть теоремы доказывается аналогично.
Для нахождения точек перегиба кривой 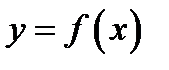 требуется:
требуется:
1)найти точки, в которых 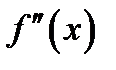 обращается в нуль или не существует;
обращается в нуль или не существует;
2)каждую такую точку исследовать с помощью достаточного признака точки перегиба;
3)найти ординаты точек перегиба, подставив их абсциссы в выражение 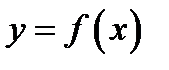 вместо
вместо 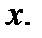
Асимптоты кривой.
Прямая называется асимптотой кривой, если расстояние от точки этой кривой до прямой стремится к нулю, когда указанная точка неограниченно удаляется от начала координат. Рассмотрим два вида асимптот.
 Вертикальные асимптоты.Дана кривая с уравнением
Вертикальные асимптоты.Дана кривая с уравнением 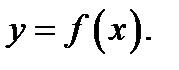 Если
Если 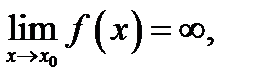
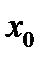 – заданное число, то кривая имеет вертикальную асимптоту с уравнением
– заданное число, то кривая имеет вертикальную асимптоту с уравнением 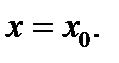 Здесь график функции будет иметь вид, указанный, например, на рис. 73.
Здесь график функции будет иметь вид, указанный, например, на рис. 73.
На кривой 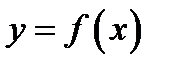 возьмём точку
возьмём точку 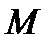 с абсциссой
с абсциссой 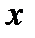 и ординатой
и ординатой 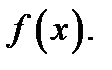 Пусть точка
Пусть точка 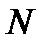 – основание перпендикуляра, опущенного из точки
– основание перпендикуляра, опущенного из точки 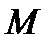 на прямую
на прямую 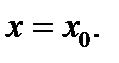 Тогда расстоя-ние от точки
Тогда расстоя-ние от точки 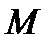 до прямой с уравне-нием
до прямой с уравне-нием 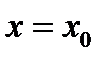 равно
равно 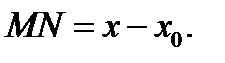
По условию при 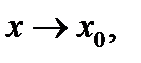 когда
когда 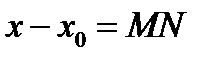 стремится к нулю, имеем
стремится к нулю, имеем 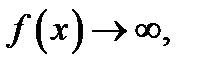 а точка
а точка 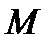 кривой неограниченно удаляется от начал координат. Иначе говоря, когда точка
кривой неограниченно удаляется от начал координат. Иначе говоря, когда точка 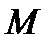 неограниченно удаляется от начала координат, расстояние
неограниченно удаляется от начала координат, расстояние 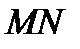 стремится к нулю. Это значит, что прямая с уравнением
стремится к нулю. Это значит, что прямая с уравнением 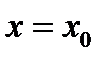 есть асимптота линии
есть асимптота линии 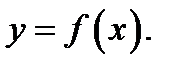
Наклонные асимптоты.Пусть кривая 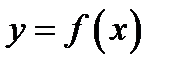 имеет наклонную асимптоту с уравнением
имеет наклонную асимптоту с уравнением 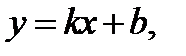 где
где 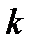 – угловой коэффициент асимптоты, т. е.
– угловой коэффициент асимптоты, т. е. 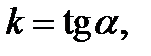 угол
угол 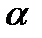 образован с осью
образован с осью 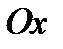 асимптотой (рис. 74). На кривой
асимптотой (рис. 74). На кривой 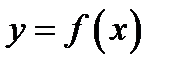 возьмём точку
возьмём точку 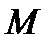 с координатами
с координатами 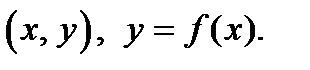 На прямой
На прямой 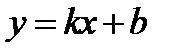 (асимптоте рассматриваемой кривой) возьмём точку
(асимптоте рассматриваемой кривой) возьмём точку 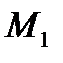 с той же абсциссой, что и у точки
с той же абсциссой, что и у точки 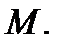 Её ордината равна
Её ордината равна 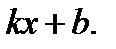 Поэтому
Поэтому
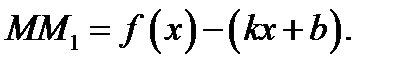 (3)
(3)
 Так как мы рассматриваем наклонную асимптоту, то считаем, что угол
Так как мы рассматриваем наклонную асимптоту, то считаем, что угол 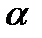 не равен
не равен 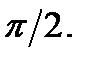 Это означает, что
Это означает, что 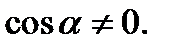 Пусть точка
Пусть точка  – основание перпендикуляра, опущен-ного из точки
– основание перпендикуляра, опущен-ного из точки  на асимптоту. Получили прямоугольный треуголь-ник
на асимптоту. Получили прямоугольный треуголь-ник 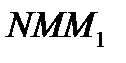 . Из него найдем выражение
. Из него найдем выражение 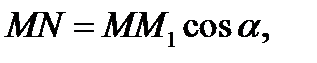 поэтому, учитывая, что
поэтому, учитывая, что 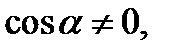 будем иметь
будем иметь
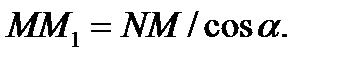 (4)
(4)
Прямая 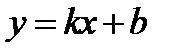 есть асимптота линии
есть асимптота линии 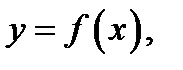 следовательно, расстояние
следовательно, расстояние  от точки
от точки  до прямой стремится к нулю, когда точка
до прямой стремится к нулю, когда точка 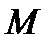 неограниченно удаляется от начала координат, т. е. её абсцисса
неограниченно удаляется от начала координат, т. е. её абсцисса 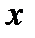 стремится к бесконечности.
стремится к бесконечности.
Итак, 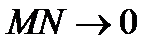 при
при 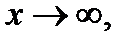 значит, согласно (4)
значит, согласно (4) 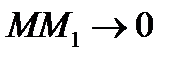 при
при 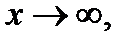 т. е.
т. е. 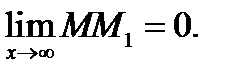 Подставим сюда вместо
Подставим сюда вместо 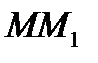 выражение (3) и получим
выражение (3) и получим
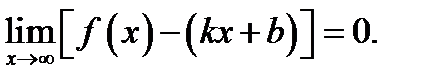 (5)
(5)
Из (5) видно, что выражение под знаком предела – бесконечно малая функция, которую обозначим через 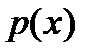 . Тогда
. Тогда 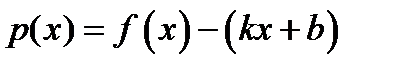 или
или 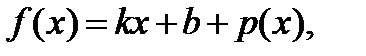 где
где 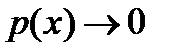 при
при 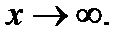 Это соотношение поделим на
Это соотношение поделим на 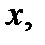 перейдем к пределу при
перейдем к пределу при 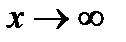 и учтем, что предел суммы есть сумма пределов. Получим
и учтем, что предел суммы есть сумма пределов. Получим
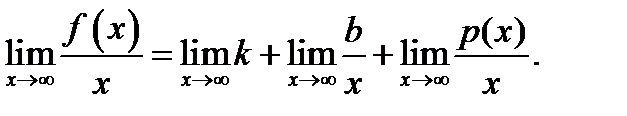
Поскольку 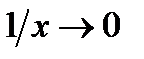 при
при 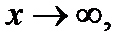 произведение постоянной
произведение постоянной 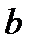 на
на 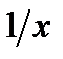 есть бесконечно малая величина, а её предел равен нулю. Аналогично
есть бесконечно малая величина, а её предел равен нулю. Аналогично 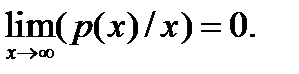 Предел постоянной
Предел постоянной  равен
равен  поэтому
поэтому
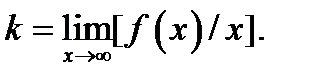 (6)
(6)
Соотношение (5) запишем так: 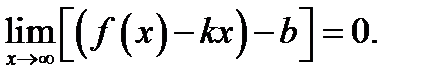 Учтём, что слева предел разности равен разности пределов и предел постоянной
Учтём, что слева предел разности равен разности пределов и предел постоянной 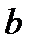 равен этой постоянной. Поэтому
равен этой постоянной. Поэтому
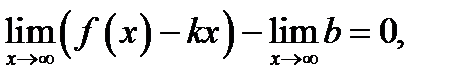
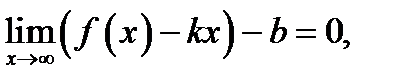
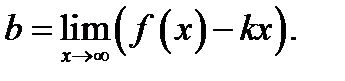 (7)
(7)
Итак, мы показали, что если линия 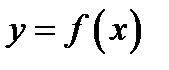 имеет наклонную асимптоту
имеет наклонную асимптоту 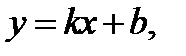 то обязательно существуют два конечных предела (6) и (7) для чисел
то обязательно существуют два конечных предела (6) и (7) для чисел 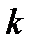 и
и 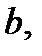 входящих в уравнение асимптоты. И наоборот, если для линии
входящих в уравнение асимптоты. И наоборот, если для линии 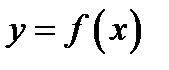 существуют два конечных предела (6), (7), то эта линия имеет наклонную асимптоту
существуют два конечных предела (6), (7), то эта линия имеет наклонную асимптоту 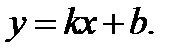 В этом можно убедиться, проведя изложенные выше рассуждения в обратном порядке.
В этом можно убедиться, проведя изложенные выше рассуждения в обратном порядке.
