Производные и дифференциалы высших порядков

На основе таблицы производных можно сделать вывод: производная любой элементарной функции также элементарная функция. Таким образом, операция дифференцирования не выводит из класса элементарных функций. Производная f(х) функции y=f(x) сама является некоторой функцией аргумента х. По отношению к ней снова можно ставить вопрос о существовании производной.

Назовем y’=f’(х) производной первого порядка функции f(х). Производная от производной (Y’)’=(f’(x))’=f’’(x) некоторой функции называется производной второго порядка этой функции. Производная от второй производной (y’’)’=(f’’(x))’=f’’’(х) называется производной третьего порядка и так далее.

Производные, начиная со второй, называются производными высших порядков:

;

…

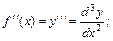
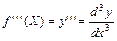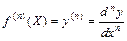
Здесь d²y, d²x – дифференциалы второго порядка;

d³y, d³x – дифференциалы третьего порядка;

dⁿy, dⁿx – дифференциалы n-го порядка

Точки экстремума функции

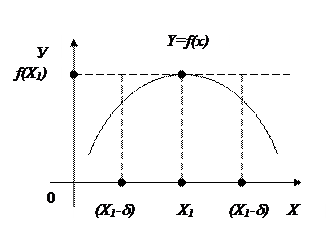
Точка x₁ называется точкой локального максимума (max) функции f(x), если для всех х из некоторой d - окрестности точки х₁ выполняется неравенство

f(x)£f(x₁)

Точка х₂ называется точкой локального минимума (min) функции f(x), если для всех х из некоторой d-окрестности точки х₂ выполняется неравенство

f(x)³f(x₂)

Локальный максимум и локальный минимум объединяют одним общим названием локальный экстремум.

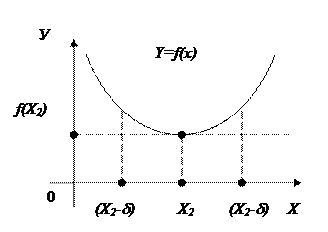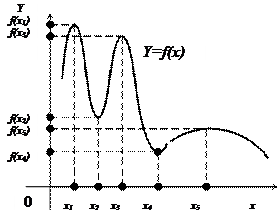
Из определения следует, что понятие экстремума носит локальный характер. Очевидно, что функция может иметь несколько локальных максимумов и несколько локальных минимумов, причем иной локальный максимум может отказаться меньше какого-то локального минимума.

Теорема Ферма (необходимое условие существования локального экстремума). Если функция y=f(x) имеет в точке x₀ локальный экстремум и дифференцируема в этой точке, то ее производная обращается в нуль в этой точке:

f’(x₀)=0

Теореме Ферма соответствует очевидный геометрический факт: если в точках максимума или минимума функция f(x) имеет производную, то касательная к графику y=f(x) в этих точках параллельна оси ОХ.

Значения аргумента, при которых производная f’(x) обращается в нуль или терпит разрыв, называются стационарными точками или точками возможного экстремума.

Теорема (условия возрастания и убывания функции)

1. Если функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b), причем f’(x)>0 при xÎ(a,b), то эта функция f(x) возрастает на отрезке [a,b] (­).

2. Если функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b), причем f’(x)<0 при xÎ(a,b), то эта функция f(x) убывает на отрезке [a,b] (¯).

Теорема (Достаточное условие существования локального экстремума). Пусть функция f(x) непрерывна в некотором интервале, содержащем стационарную точку x₀ и дифференцируема во всех точках этого интервала, кроме, может быть, самой точки x₀.

Если при переходе слева на право через эту точку производная f’(x) меняет знак с плюса на минус, то при x=x₀ функция f(x) имеет локальный максимум.

Таким образом, если

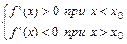, то при x=x₀ f(x) имеет локальный максимум

Если при переходе через точку X₀ слева направо производная f’(x) меняет знак с минуса на плюс, то функция f(x) имеет в этой точке локальный минимум.

Таким образом, если

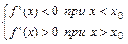то при x=x₀ f(x) имеет локальный минимум.

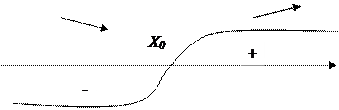
Если при переходе через точку X₀ слева направо производная f’(x) не меняет знак, то в точке x=x₀ экстремума не существует.

		X0

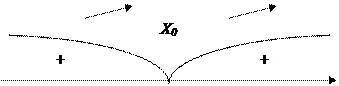Пример. Найти экстремумы следующих функции или показать, что

функция не имеет экстремумов:

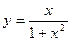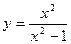а) , б) , в)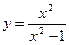

Решение.

а)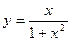

Область определенная этой функции – вся числовая прямая: xÎRe

Найдем производную и приравняем ее к нулю:

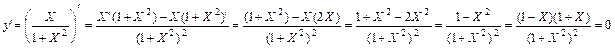
Решая получившееся уравнение (1-X)(1+X)=0, находим две стационарные точки: x₁=-1, x₂=1.

Исследуя знак производной y’ в окрестностях этих точек

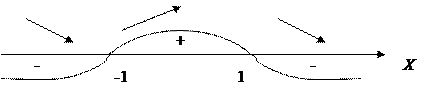заключаем, что х=-1 – точка локального минимума,

х=1 – точка локального максимума

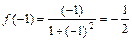- минимальное значение функции,

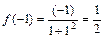- максимальное значение функции.

б)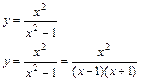

Область определения этой функции – вся числовая прямая за исключением точек х=-1 и х=1, таким образом

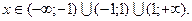
Найдем производную и приравняем ее к нулю:

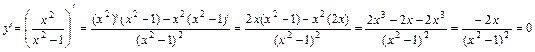
Решая получившееся уравнение–2х=0, находим одну стационарную точку: х=0.

Исследуя знак производной в окрестности этой точки

Заключаем, что х=0 – точка локального максимума.

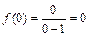- максимальное значение функции.

в)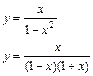

Область определения этой функции– вся числовая прямая за исключением точек х=-1 и х=1. Таким образом

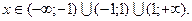
Найдем производную и приравняем ее к нулю:

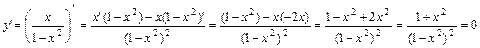
Получившееся уравнение1+х²=0 решений не имеет, значит стационарных точек нет и данная функция экстремума не имеет.