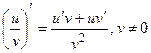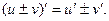Первый замечательный предел

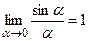
Второй замечательный предел

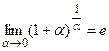или

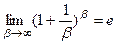
Вычисление предела сводится к подстановке в данное выражение предельного значения аргумента. Если при этом получаем неопределенности типа 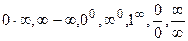, то вычисление этого предела в этом случае называется раскрытием неопределенности.

Пример. Найти предел:

1. 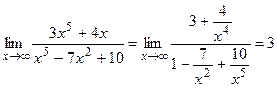, здесь раскрываем неопределенность типа 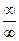, поделив числитель и знаменатель на 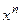, где n = 5 (наивысшая степень х).

2. 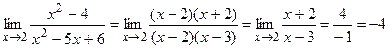, здесь раскрыта неопределенность типа 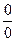, поделив числитель и знаменатель на (х-2).

3.

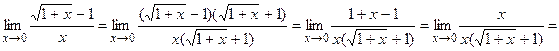
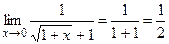= ,здесь, раскрывая неопределенность 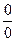, избавились от иррациональности, умножив числитель и знаменатель на сопряженный множитель .

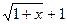4.

= .

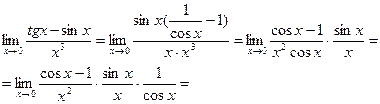
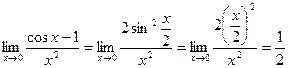В этом примере неопределенность 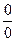раскрыли, используя первый замечательный предел и формулы эквивалентности.

5.

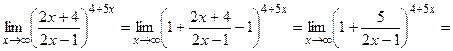
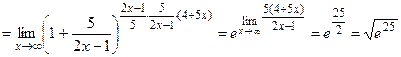
в этом примере неопределенность 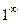раскрывается с помощью второго замечательного предела.

Непрерывность функции

Функция называется f(x) называется непрерывной в точке х₀, , если она определена в некоторой окрестности этой точки и выполняется равенство

,

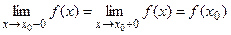где 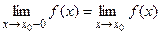, 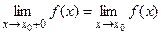односторонние (левый и правый) пределы .

Если хотя бы одно из этих условий не выполняется, то функция называется разрывной в точке х0 .

Когда у функции f(x) имеются односторонние пределы 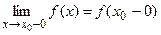и 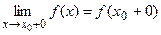и не все числа f(x0) , f(x0 - 0) и f(x0 + 0) равны между собой , то разрыв в точке х0 называется разрывом I рода. Величина 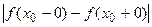называется скачком функции.

Если 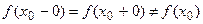, то разрыв в точке называется устранимым. Здесь полагая 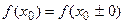получают функцию непрерывную в точке х0.

Если хотя бы один из односторонних пределов 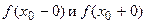не существует или равен бесконечности, то разрыв называется разрывом II рода.

Если функция непрерывна в каждой точке некоторого промежутка, то она называется непрерывной на этом промежутке.

Алгебраическая сумма, произведение и суперпозиция конечного числа непрерывных функций есть функция непрерывная. Отношение двух непрерывных функций есть функция непрерывная, если знаменатель не равен нулю. Отсюда следует, что всякая элементарная функция непрерывна в точках, в которых она определена.

Пример. Исследовать на непрерывность:

1. 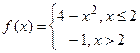имеет в точке х=2 разрыв I рода, поскольку 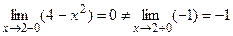. Скачек функции в точке х=2 равен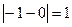

.

2. Функция f(x) = 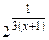не определена в точке х = -1, потому в этой точке она имеет разрыв. Поскольку 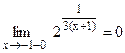и 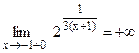, то в точке х = -1 функция имеется разрыв II рода.

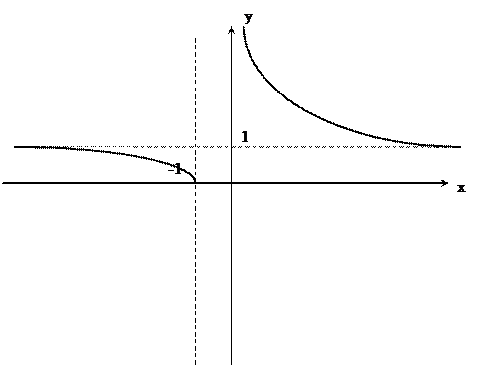Дифференциальное исчисление.

Производная. Техника дифференцирования.

Обозначение

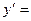
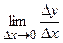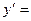
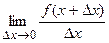Производной функции у = f(x) в точке х0 называется предел или , где 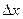= x2 –x1 – приращение аргумента, 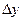= у2 – у1 - приращение функции на отрезке [x1, x2]. Функция f(x) называется дифференцированной в точке х, если в этой точке существует производная 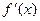. Геометрически производная представляет собой угловой коэффициент касательной к графику функции у = f(x) в точке х, т. е. 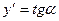. Если функция дифференцируема в каждой точке промежутка Х, то ее называют дифференцированной на промежутке Х.

Основные правила дифференцирования.

Будем считать, что u=u(x) и v=v(x) – дифференцируемые функции, а С – постоянная. Тогда:

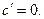4.

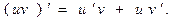
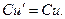5.