Упражнения для выполнения
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ

 Множество – основное математическое понятие. В обычной жизни его смысл заложен в словах: «совокупность», «класс», «стая», «табун», «стадо» и т.п. Теория множеств как математическая дисциплина создана немецким математиком Г. Кантором, которая получила признание в качестве самостоятельного раздела математики к 1890 году, когда были получены ее приложения в анализе и геометрии. Главная заслуга Георга Кантора заключается в установлении того факта, что понятие бесконечность является не абстракцией, придуманной философами, а реальностью; бесконечные совокупности предметов существуют наравне с конечными.
Множество – основное математическое понятие. В обычной жизни его смысл заложен в словах: «совокупность», «класс», «стая», «табун», «стадо» и т.п. Теория множеств как математическая дисциплина создана немецким математиком Г. Кантором, которая получила признание в качестве самостоятельного раздела математики к 1890 году, когда были получены ее приложения в анализе и геометрии. Главная заслуга Георга Кантора заключается в установлении того факта, что понятие бесконечность является не абстракцией, придуманной философами, а реальностью; бесконечные совокупности предметов существуют наравне с конечными.
Множество относится к математическим объектам, для которых нет строго определения. Мы можем лишь в какой-то мере дать описание основных его свойств.
Кантор описывает множество следующим образом:
| Определение. | Множество S есть любое собрание определенных и различимых между собой объектов нашей интуиции и интеллекта, мыслимое как единое целое. |
¢ Понятие множества. Способы задания множества
Мы под множеством будем понимать следующее:
| Определение. | Множество – набор (совокупность) определенных, различимых между собой объектов, рассматриваемых как единое целое, и обладающий некоторым общим свойством. 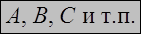 . Объекты, составляющие данное множество, называют его элементами. . Объекты, составляющие данное множество, называют его элементами. 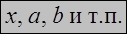 . . |
Для того, чтобы указать, что х – элемент множества А, записывают 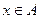 и читают «х принадлежит А». Чтобы указать, что х не является элементом множества А, записывают
и читают «х принадлежит А». Чтобы указать, что х не является элементом множества А, записывают 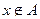 и читают «х не принадлежит множеству А».
и читают «х не принадлежит множеству А».
Для ряда числовых множеств в математике приняты стандартные обозначения:
| Обозначения числовых множеств: 1) N – множество натуральных чисел. 2) Z – множество целых чисел. 3) Q – множество рациональных чисел (дроби). 4) R – множество действительных чисел |
Существует два способа задания множества:
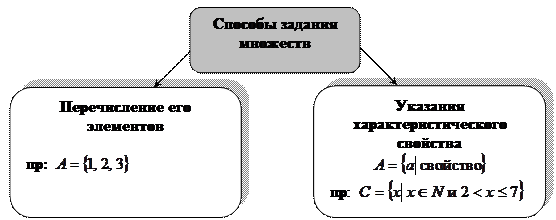
Рисунок 1. Способы задания множеств
Множества можно разделить на конечные и бесконечные.
| Определение. | Конечным множеством называется множество, состоящее из конечного числа элементов. Множество называется бесконечным, если оно состоит из бесконечного числа элементов |
Пример 1.
· Конечные множества: множество букв алфавита, множество студентов 2 курса специальности «Юриспруденция» и т.д.
· Бесконечные множества: множество натуральных чисел, множество точек прямой и т.д.
К конечным множествам относится и множество, не содержащее элементов вообще. Такое множество называют пустым и обозначают Ø.
Пример 2.
Ø = 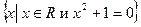 , поскольку среди действительных чисел нет решения данного уравнения.
, поскольку среди действительных чисел нет решения данного уравнения.
| Определение. | Если каждый элемент множества В является также и элементом множества А, то говорят, что множество В называется подмножеством множества А. 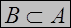 (В включено в А). (В включено в А). |
Пример 3.
Множество 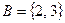 ,
, 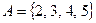 , тогда
, тогда 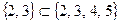 , т.е.
, т.е. 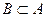 .
.
Основные свойства включений: 1) Каждое множество есть подмножество самого себя: 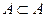 . 2) Если . 2) Если 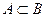 , , 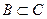 , то , то 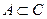 . 3) Пустое множество есть подмножество любого множества: Ø . 3) Пустое множество есть подмножество любого множества: Ø 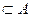 . 4) Каждое не пустое множество . 4) Каждое не пустое множество 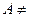 Ø имеет по крайней мере два различных подмножества: само А и пустое множество Ø. 5) Каждый элемент множества А определяет некоторое подмножество множества А: если Ø имеет по крайней мере два различных подмножества: само А и пустое множество Ø. 5) Каждый элемент множества А определяет некоторое подмножество множества А: если 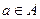 , то , то 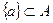 . . |
| Определение. | Множества А и В называются равными (или совпадающими), если они состоят из одних и тех же элементов, т.е. 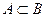 и и 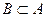 . . 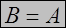 |
Если множества не равны, то пишут 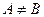 .
.
Пример 4.
Множества 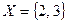 и
и 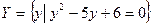 , где
, где 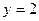 и
и 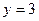 удовлетворяют уравнению
удовлетворяют уравнению 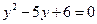 , т.е.
, т.е. 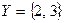 , значит
, значит 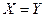 .
.
| Определение. | Множество всех подмножеств множества А называется множеством-степенью множества А. 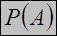 |
Пример 5.
Пусть 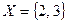 , тогда
, тогда 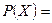 {
{ 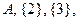 Ø}, т.е. если множество состоит из двух элементов, то множество-степень состоит из четырех подмножеств.
Ø}, т.е. если множество состоит из двух элементов, то множество-степень состоит из четырех подмножеств.
Пусть 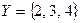 , тогда
, тогда 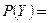 {
{ 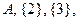 {4}, {2,3}, {3,4}, {2,4}, Ø}, т.е. если множество состоит из трех элементов, то множество-степень состоит из восьми подмножеств.
{4}, {2,3}, {3,4}, {2,4}, Ø}, т.е. если множество состоит из трех элементов, то множество-степень состоит из восьми подмножеств.
Таким образом, если конечное множество А состоит из n элементов, то число всех его подмножеств равно 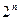 .
.
| Определение. | Множество U называется универсальным для системы множеств А, B, C, …, если каждое множество системы является подмножеством U, т.е. 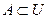 , , 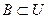 , , 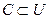 , …. . , …. . 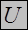 |
 ¢ Операции над множествами
¢ Операции над множествами
 Если имеются два (или более) множества, то на основе их можно получить новые множества при помощи операций (отношений) над ними. Геометрически, для наглядного представления, данные отношения можно представить при помощи кругов, которые один из первых использовал для решения задач Г.Лейбниц, затем развил их применение Леонард Эйлер и особенного расцвета достигшие в сочинениях английского логика Джона Венна, поэтому такие схемы иногда называют Диаграммы Эйлера-Венна.
Если имеются два (или более) множества, то на основе их можно получить новые множества при помощи операций (отношений) над ними. Геометрически, для наглядного представления, данные отношения можно представить при помощи кругов, которые один из первых использовал для решения задач Г.Лейбниц, затем развил их применение Леонард Эйлер и особенного расцвета достигшие в сочинениях английского логика Джона Венна, поэтому такие схемы иногда называют Диаграммы Эйлера-Венна.
Диаграммы используются в математике, логике, менеджменте, особое применение они нашли в современной логико-математической теории «формальных нейронных сетей».
 На Диаграммах Эйлера-Венна универсальное множество U изображается в виде прямоугольника, его подмножества – в виде кругов (реже прямоугольников), а элементы принадлежащие данным подмножествам в виде точек (см. Рисунок 2).
На Диаграммах Эйлера-Венна универсальное множество U изображается в виде прямоугольника, его подмножества – в виде кругов (реже прямоугольников), а элементы принадлежащие данным подмножествам в виде точек (см. Рисунок 2).
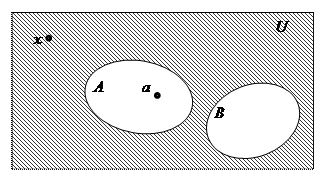
Рисунок 2. Пример диаграммы Эйлера-Венна
Рассмотрим операции над множествами, некоторые из которых (объединение и пересечение) аналогичны операциям сложения и умножения целых чисел.
Операции пересечение и объединение множеств выполняются для любой пары множеств. Операция дополнение имеет смысл для тех множеств, когда второе является подмножеством первого.
Следует провести аналогию между логическими операциями и операциями над множествами.
| Высказывание | Множество |
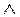 (конъюнкция) (конъюнкция) | Пересечение 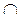 |
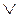 (дизъюнкция) (дизъюнкция) | Объединение 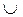 |
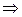 (импликация) (импликация) | Разность 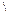 |
 (отрицание) (отрицание) |  ( дополнение) ( дополнение) |
| тавтология | 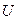 (универсальное множество) (универсальное множество) |
| противоречие | Ø (пустое множество) |
Множества вместе с определенными на них операциями образуют алгебру множеств. Последовательность выполнения операций задается с помощью формулы алгебры множеств. Например, 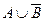 ,
, 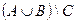 – формулы алгебры множеств.
– формулы алгебры множеств.
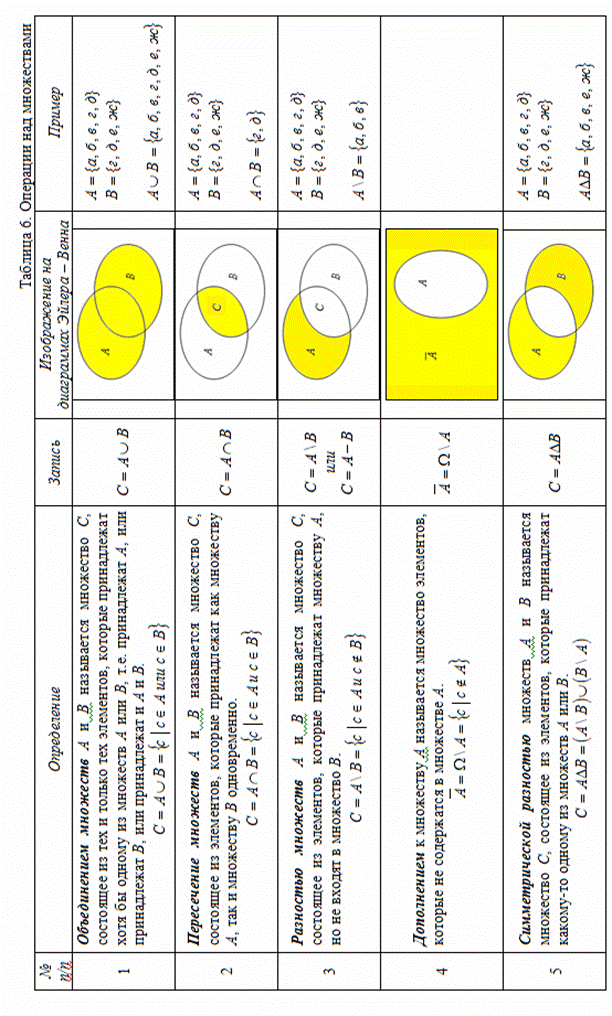
¢ Основные законы над множествами
Законы: 1) Закон идемпотентности: a) 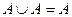 б) б) 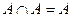 2) Закон коммутативности: a) 2) Закон коммутативности: a) 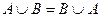 б) б) 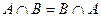 3) Закон ассоциативности: a) 3) Закон ассоциативности: a) 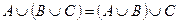 б) б) 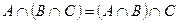 4) Закон дистрибутивности: a) 4) Закон дистрибутивности: a) 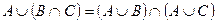 б) б) 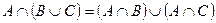 5) Закон поглощения: a) 5) Закон поглощения: a) 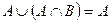 б) б) 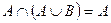 6) Закон де Моргана: a) 6) Закон де Моргана: a) 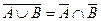 б) б) 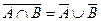 7) Закон двойного отрицания: 7) Закон двойного отрицания: 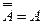 8) 8) 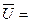 Ø 9) Законы для объединения, пересечения и дополнения: а) Ø 9) Законы для объединения, пересечения и дополнения: а) 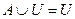 ; б) ; б) 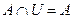 ; в) ; в) 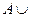 Ø = A; г) Ø = A; г) 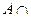 Ø = Ø; д) Ø = Ø; д) 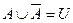 ; е) ; е) 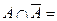 Ø 10) Ø 10) 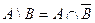 11) Законы для разностей: а) 11) Законы для разностей: а) 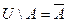 ; б) ; б) 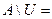 Ø; в) Ø; в) 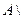 Ø = A; г) Ø Ø = A; г) Ø 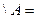 Ø; д) Ø; д) 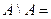 Ø Ø |
Доказательство каждого из перечисленных законов основано на определении равенства множеств и определений операций над множествами. Чтобы доказать некоторое тождество A = B, нужно доказать, что, во-первых, если xÎ А, то xÎВ и, во-вторых, если xÎВ, то xÎ А. Докажем один из этих законов: 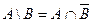 .
.
Пусть 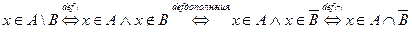 [1]. Таким образом, мы взяли произвольный элемент
[1]. Таким образом, мы взяли произвольный элемент 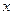 из
из 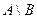 и при помощи равносильных преобразований получили, что он принадлежит
и при помощи равносильных преобразований получили, что он принадлежит 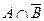 , т.е.
, т.е. 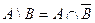 .
.
И действительно это так, проиллюстрируем это на диаграммах Эйлера-Венна (см. Рисунок 3).
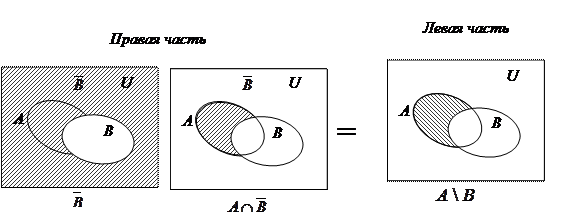
Рисунок 3. Пример иллюстрации равенства множеств 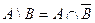 на диаграммах Эйлера-Венна
на диаграммах Эйлера-Венна
Пример 6.
Пусть А, В и С произвольные множества. Докажите, что 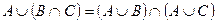 (закон дистрибутивности).
(закон дистрибутивности).
Пусть 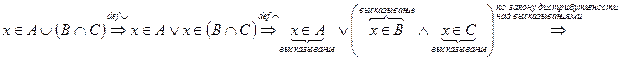
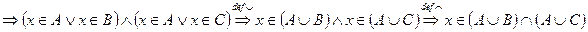 ,т.е.
,т.е. 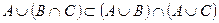 .
.
Пусть
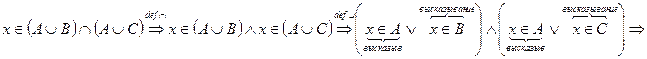
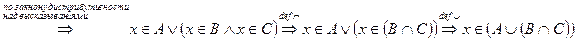 , т.е.
, т.е. 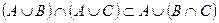 .
.
Так как 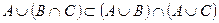 и
и 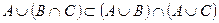 , значит
, значит 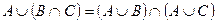 .
.
Основные законы алгебры множеств можно использовать для доказательства других тождеств.
Пример 7.
Докажите равенство 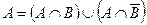 .
.
Решение.
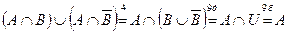 , что и требовалось доказать.
, что и требовалось доказать.
¢ Формула включений и исключений
После определения операций и основных законов над множествами возникает вопрос относительно числа элементов полученных множеств.
Пусть дано конечное не пустое множество А, т.е. 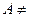 Ø, состоящее из n элементов. Закрепим за каждым элементом множества А соответствующий номер 1, 2, 3, …, n. Тогда элементы множества А предстанут в занумерованном виде:
Ø, состоящее из n элементов. Закрепим за каждым элементом множества А соответствующий номер 1, 2, 3, …, n. Тогда элементы множества А предстанут в занумерованном виде: 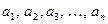 , где номер последнего элемента и означает число элементов множества А. Значит число n, соответствующее количеству элементов множества
, где номер последнего элемента и означает число элементов множества А. Значит число n, соответствующее количеству элементов множества 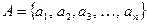 , будет количественной характеристикой данного множества. Число элементов конечного множества А будем обозначать
, будет количественной характеристикой данного множества. Число элементов конечного множества А будем обозначать 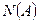 . Число элементов пустого множества Ø равно нулю, т.е.
. Число элементов пустого множества Ø равно нулю, т.е. 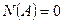 .
.
Пусть существуют множества А и В, количество элементов которых 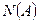 и
и 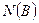 , тогда общее количество элементов А и В вычисляет формула, называемая формулой включений и исключений[2] (ее можно обобщить на три и более множества), которая позволяет решать многие задачи теории множеств (см. Рисунок 4).
, тогда общее количество элементов А и В вычисляет формула, называемая формулой включений и исключений[2] (ее можно обобщить на три и более множества), которая позволяет решать многие задачи теории множеств (см. Рисунок 4).
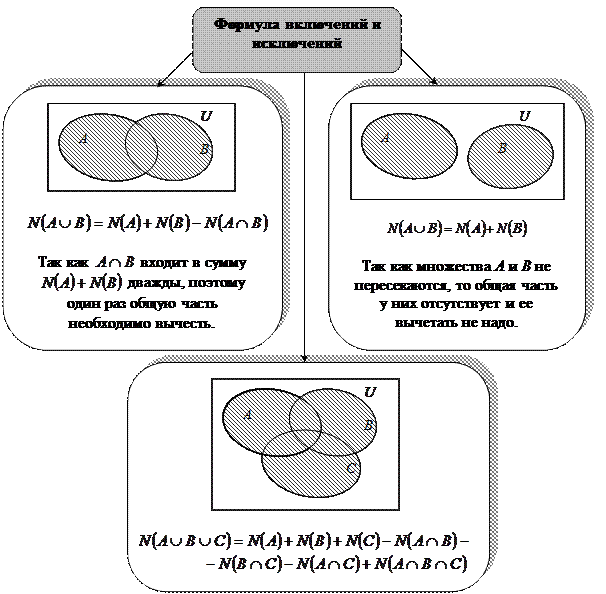
Рисунок 4. Формула включений и исключений.
Пример 7.
Из 16 студентов группы, изучающих английский или китайский язык, 11 – изучают китайский. Сколько студентов изучают оба языка, если английский язык изучают 9 из них?
Решение.
Что дано?
Даны два множества:
К – студенты, изучающие китайский язык, которых 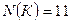 .
.
А – студенты, изучающие английский язык, которых 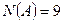 .
.
Всего студентов 16, т.е. 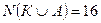 .
.
Что нужно сделать? Узнать сколько студентов изучают оба языка одновременно (и китайский, и английский), т.е. 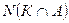 (см. рисунок 5).
(см. рисунок 5).
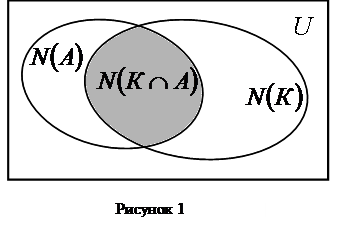
Значит, количество студентов в группе изучающих оба языка можно вычислить по формуле включений и исключений:
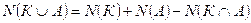 , т.е.
, т.е. 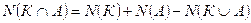
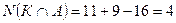 .
.
Ответ. 4 человека изучают оба языка: китайский и английский язык.
Упражнения для выполнения
1) Приведите примеры множеств из обычной жизни. Какие множества, из приведенных примеров, является конечными, а какие нет. Поясните свой ответ.
2) Запишите, используя символы:
а) число 12 – натуральное;
б) число – 6 – не является натуральным;
в) число 0 является рациональным;
г) число 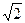 - действительное.
- действительное.
3) Прочитайте следующие высказывания и укажите среди них верные, поясните свой ответ:
| а) | 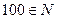 ; ; | г) | 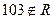 ; ; | ж) | 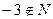 ; ; |
| б) | 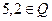 ; ; | д) | 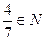 ; ; | з) | 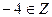 ; ; |
| в) | 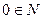 ; ; | е) | 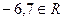 ; ; | и) | 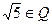 . . |
4) Перечислите элементы следующих множеств:
а) А – множество нечетных однозначных множеств;
б) В – множество натуральных чисел меньших или равных13;
в) С – множество двухзначных чисел, делящихся на 5.
5) Задайте множество D, которое состоит из натуральных чисел:
а) кратных 3;
б) больших 40, но меньших 70;
в) не больших 13;
г) четных двухзначных чисел;
д) по крайней мере равных 10.
6) Укажите характеристическое свойство элементов множества:
а) {а, е, ё, и, о, у, э, ю, я, ы};
б) {60, 62, 64, 66, 68};
в) {111, 222, 333, 444, 555, 666, 777, 888, 999}.
7) Задайте при помощи характеристического свойства множества, выделенные на координатной прямой:
| а) |  | в) |  |
| б) |  | г) |  |
8) Опишите множество точек М плоскости таких, что:
а) 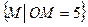 ;
;
б) 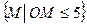 ;
;
в) 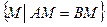 .
.
9) Какое число лишнее в ряду: 470, 720, 330, 400, 510, 640?
10) Истинными являются высказывания …. Почему?
а) 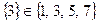 ;
;
б) Ø 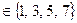 ;
;
в) 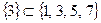 ;
;
г) 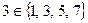 ;
;
д) Ø 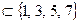 ;
;
е) 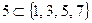 .
.
11) Определите, какой знак «=», « 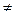 », «
», « 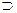 », «
», « 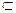 » или «
» или « 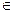 » можно поставить вместо знака «?», чтобы полученное утверждение было верно:
» можно поставить вместо знака «?», чтобы полученное утверждение было верно:
а) {1, 3} ? {1, 2, 3};
б) {3} ?{1, 3, 5, 8};
в) {{1, 2}, {2, 3}, {1, 3}} ? {1, 2, 3};
г) 1 ? {1, 3, 5, 8};
д) {1, 3} ? {{1, 3}, 2};
е) {{1, 2}, {2, 3}, {1, 3}}?{(1, 2), (2, 3), (1, 3)};
ж) Ø ?{1, 3, 5, 8};
з) {3} ?{1, {3}, 5, 8};
и) {(2, 1), (3, 2)} ? {(1, 2), (2, 3)};
к) {{1, 2}, {2, 3}} ? {{2, 1}, {3, 2}, {1, 3}};
л) {1, 2, 3} ? {x | x делится на 6}.
12) Может ли у множества быть:
а) 0 подмножеств;
б) 9 подмножеств;
в) 16 подмножеств.
Если да, то ответьте на вопросы: «Почему?» и «Из скольких элементов состоит множество, у которого имеется заданное количество подмножеств?».
13) Приведите пример таких множеств А, В и С, что 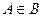 ,
, 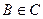 и
и 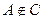 .
.
14) Может ли при некоторых А, B, C и D выполняться набор условий: 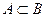 ,
, 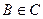 ,
, 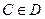 и
и 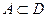 .
.
15) Изобразите при помощи диаграмм Эйлера-Венна отношения между множествами C и D, если:
а) C – множество двухзначных чисел и 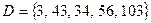 ;
;
б) C – множество двухзначных чисел и D – множество четных натуральных чисел;
в) C – множество двухзначных чисел и D – множество трехзначных чисел;
г) C – множество двухзначных чисел и D – множество натуральных чисел, не меньших 10.
16) Найдите объединение, пересечение, разность и симметрическую разность множеств А и В, если:
а) А = {1, 2, 3, 4, 5}, В ={2, 4, 6, 8, 10};
б) А = {а, б, в, г, д, е}, В = {а, в, д, к, и}.
17) Найдите объединение, пересечение, разность и симметрическую разность множеств А и В, если:
а) 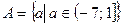 ,
, 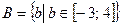 ;
;
б) 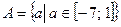 ,
, 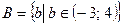 .
.
18) Студентам предложено начертить две фигуры, принадлежащие объединению и пересечению множеств Х и Y, если:
| № п/п | Х | У | 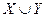 | 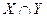 |
| множество ромбов | множество прямоугольников | |||
| множество равнобедренных треугольников | множество прямоугольных треугольников |
19) Отношения между множествами всех выпуклых четырехугольников, параллелограммов, прямоугольников, ромбов и квадратов изображены на Рисунок 6. Чем является множества А, B, C и D.
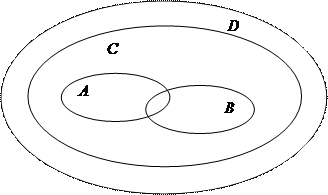
Рисунок 6
20) Даны множества:
А – множество натуральных чисел, кратных 2,
B – множество натуральных чисел, кратных 6,
С – множество натуральных чисел, кратных 3.
Задайте множества А, B и C. Как между собой связаны множества А, B и C? Покажите это на диаграммах Эйлера-Венна.
21) Даны следующие числовые множества:
А = {1, 3, 5, 7, 9,11},
В ={2, 5, 6, 11, 12},
С={1, 2, 3, 5, 9, 12}.
Найдите множества, которые будут получены в результате выполнения следующих операций:
| а) | 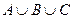 ; ; | д) | 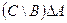 ; ; |
| б) | 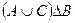 ; ; | е) | 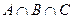 ; ; |
| в) | 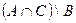 ; ; | ж) | 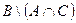 ; ; |
| г) | 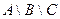 ; ; | з) | 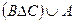 . . |
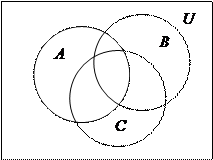
22) Укажите ту часть диаграммы, которая соответствует следующему множеству:
| а) | 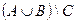 ; ; | д) | 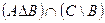 ; ; |
| б) | 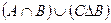 ; ; | е) | 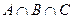 ; ; |
| в) | 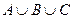 ; ; | ж) | 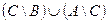 ; ; |
| г) | 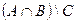 ; ; | з) | 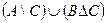 . . |
23) Запишите множество, изображенное с помощью диаграммы Эйлера-Венна на Рисунок 7:
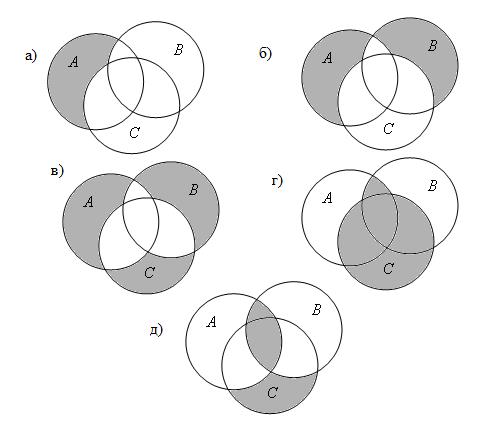
Рисунок 7
24) Заполните пустые клетки в таблице, если даны следующие множества:
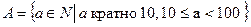 ,
,
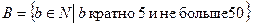 .
.
| № п/п | Словесная формулировка множества | Элементы множества | Отношение между множествами | Диаграммы Эйлера-Венна |
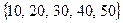 | ||||
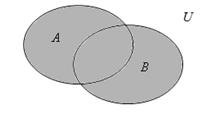 | ||||
| Ø | ||||
| множество, являющееся дополнением множества А до В |
25) Пусть даны два множества А и В таких, что 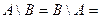 Ø. Можно ли выразить данное отношение более простым способом. Ответ свой проиллюстрируйте диаграммами Эйлера-Венна.
Ø. Можно ли выразить данное отношение более простым способом. Ответ свой проиллюстрируйте диаграммами Эйлера-Венна.
26) Каким условием связаны два множества 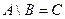 и
и 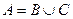 необходимым, достаточным или необходимым и достаточным? Ответ свой проиллюстрируйте диаграммами Эйлера-Венна.
необходимым, достаточным или необходимым и достаточным? Ответ свой проиллюстрируйте диаграммами Эйлера-Венна.
27) Покажите на диаграммах Эйлера-Венна верность данных равенств, после чего докажите, что они равны:
а) 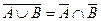 ;
;
б) 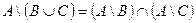 .
.
28) Упростите выражения:
| а) | Ø 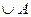 ; ; | з) | 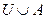 ; ; |
| б) | Ø 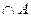 ; ; | и) | 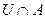 ; ; |
| в) | Ø 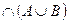 ; ; | к) | 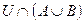 ; ; |
| г) | Ø 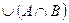 ; ; | л) | 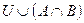 ; ; |
| д) | 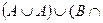 Ø); Ø); | м) | 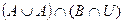 ; ; |
| е) | 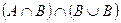 ; ; | н) | 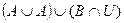 . . |
| ж) | 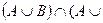 Ø); Ø); |
29) Запишите выражение в более простом виде:
| а) | 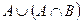 ; ; | ж) | 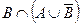 ; ; |
| б) | 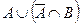 ; ; | з) | 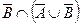 ; ; |
| в) | 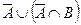 ; ; | и) | 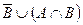 ; ; |
| г) | 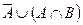 ; ; | к) | 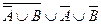 ; ; |
| д) | 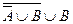 ; ; | л) | 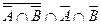 . . |
| е) | 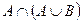 ; ; |
30) Упростите выражения:
а) 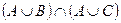 ;
;
б) 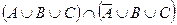 ;
;
в) 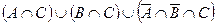 ;
;
г) 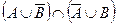 ;
;
д) 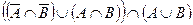 .
.
31) Докажите равенства:
а) 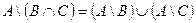 ;
;
б) 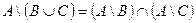 ;
;
в) 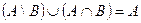 ;
;
г) 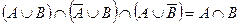 ;
;
д) 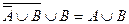 ;
;
е) 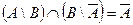 ;
;
ж) 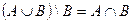 ;
;
з) 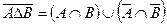 ;
;
32) Выясните, при каком условии множества Х удовлетворяет условию:
а) 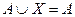 ;
;
б) 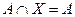 .
.
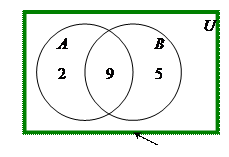
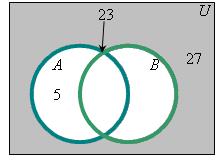
33) По предложенным диаграммам определите соответственные значения:
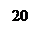  |  |
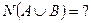 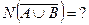  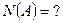 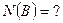 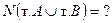 | 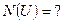 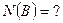 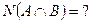 |
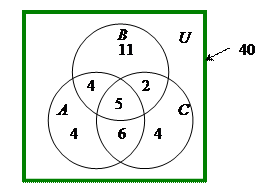 | 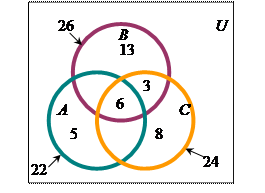 |
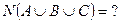 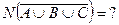 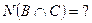 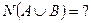 | 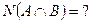 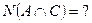 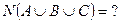 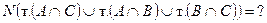 |
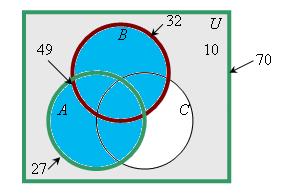 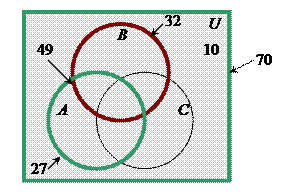 | |
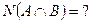 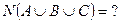 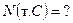 |
34) Правильно ли представлено на Рисунок 8 условие следующей задачи: «Из 100 человек английский язык изучают 28, немецкий – 30, французский – 42, английский и немецкий – 8, английский и французский – 10, немецкий и французский – 5. Все три языка изучают 3 студента».
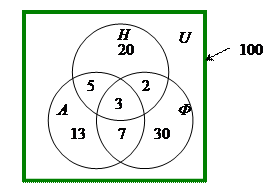
Рисунок 8
35) В рамках задачи 34 ответьте на вопросы: «Сколько студентов изучают только один язык?», «Сколько студентов не изучают не один язык?».
36) В третьем классе дети коллекционируют марки и монеты. Марки коллекционируют 8 человек, монеты – 5 человек. Всего коллекционеров 11. Объясните, как это может быть. Сколько человек коллекционируют только марки? Сколько человек коллекционируют только монеты?
37) На первом курсе учатся 100 студентов. Из них 60 изучают английский язык, 50 – французский язык, 50 – немецкий язык, 30 – английский и французский языки, 30 – английский и немецкий языки, 20 – немецкий и французский языки, 10 – все три языка.
Изобразите графически данные задачи и установите, сколько студентов:
а) изучают только английский язык;
б) изучают английский и французский языки, но не изучают немецкий язык;
в) изучают два языка;
г) не изучают ни одного из тех языков.
38) Даны 40 чисел. Из них 10 чисел кратны 3, 15 кратны 2, 20 чисел не кратны ни 2, ни 3. Сколько среди данных 40 чисел, кратных 6?
39) В спортивном лагере 100 человек, занимающихся плаванием, легкой атлетикой и лыжами. Из них 10 занимаются и плаванием, и легкой атлетикой, и лыжами, 18 – плаванием и легкой атлетикой, 15 – плаванием и лыжами, 21 – легкой атлетикой и лыжами. Число спортсменов, занимающихся плаванием, равно числу спортсменов, занимающихся легкой атлетикой, и равно числу спортсменов, занимающихся лыжами. Найти число спортсменов, которые занимаются только лыжным спортом или только легкой атлетикой.
40) На первом курсе в одной группе учатся 40 курсантов. Из них по теории государства и права имеют тройки 19 человек, по информатике и математике —17 человек и по физкультуре –22 человека. Только по одному предмету имеют «3»: по теории государства и права –4 человека, по информатике и математике –4 человека и по физкультуре –11 человек. 7 человек имеют «3» и по информатике и математике, и по физкультуре, из них 5 имеют «3» и по теории государства и права. Сколько человек учится без «3»? Сколько человек имеют «3» по двум из трех дисциплин?
41) В классе 20 человек. На экзаменах по истории, математике и литературе 10 учеников не получили ни одной пятерки, 5 учеников получили 5 по истории, 5 – по математике и 4 – по литературе; 2 - по истории и математике, 2 - по истории и литературе, 1 - по математике и литературе. Сколько учеников получили 5 по всем предметам?
42) Опрос 100 студентов дал следующие результаты о количестве студентов, посещающих кружки: только спортивную секцию посещают 18; занимаются спортом и не ходят в драматический кружок – 23; занимаются спортом и танцами – 8; занимаются спортом – 26; посещают танцы – 48; ходят на танцы и в драматический кружок 8; не посещают никакие кружки – 24.
а) Сколько студентов, занимающихся спортом, посещает драматический кружок?
б) Сколько студентов занимается в драматическом кружке?
в) Сколько студентов занимаются танцами, в том и только том случае, если они не посещают драматический кружок?
[1] def – это действие по определению.
[2] Впервые формулу включений и исключений опубликовал португальский математик Даниэль да Сильва в 1854 года. Но еще в 1713 году Николай Бернулли использовал этот метод для решения задачи о встречах.
