Вычисление площадей плоских фигур с помощью определенного интеграла
Пусть функция 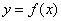 неотрицательна и непрерывна на отрезке
неотрицательна и непрерывна на отрезке 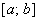 . Тогда по геометрическому смыслу определенного интеграла площадь S под кривой
. Тогда по геометрическому смыслу определенного интеграла площадь S под кривой 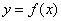 на
на 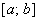 численно равна определенному интегралу
численно равна определенному интегралу 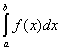 , т.е.
, т.е. 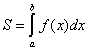 .
.
Пример:
Найти площадь фигуры, ограниченной линиями 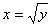 ,
, 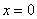 ,
, 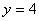 .
.
Из Рис. 1 видно, что площадь криволинейного треугольника ОАВ равна разности двух площадей: 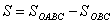 . Решая систему
. Решая систему 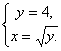 , получаем координаты точки В (точки пересечения кривой
, получаем координаты точки В (точки пересечения кривой 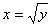 и прямой
и прямой 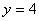 ) В
) В 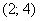 . Тогда
. Тогда 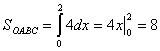 ,
, 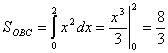 .
.
Окончательно 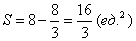 .
.
Отметим, что данная задача может быть решена другим способом.
По определению определенного интеграла 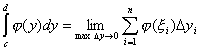 .
.
Это равенство можно понимать так, что при построении интегральной суммы разбиению подвергается отрезок 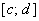 оси ординат. Соответственно точки
оси ординат. Соответственно точки 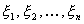 - это ординаты, фиксированные на каждом из отрезков разбиения. Поэтому, если
- это ординаты, фиксированные на каждом из отрезков разбиения. Поэтому, если 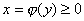 на
на 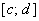 , то интеграл
, то интеграл 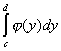 численно равен площади криволинейной трапеции, ограниченной кривой
численно равен площади криволинейной трапеции, ограниченной кривой 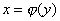 и прямыми
и прямыми 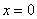 ,
, 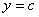 ,
, 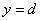 .
.
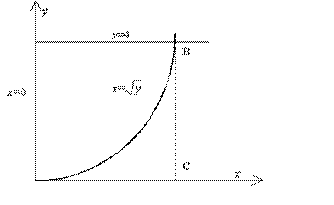
Рис. 1
Возвращаясь к нашей задаче, можно посчитать площадь следующим образом:
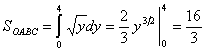 .
.
Если функция 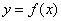 не положительна и непрерывна на отрезке
не положительна и непрерывна на отрезке 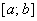 , то площадь
, то площадь 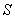 над кривой
над кривой 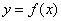 на
на 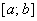 отличается знаком от определенного интеграла
отличается знаком от определенного интеграла 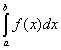 :
:
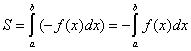 .
.
Пример:
Найти площадь фигуры, ограниченной линиями 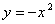 ,
, 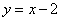 ,
, 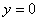 .
.
Из Рис. 2 видно, что искомая площадь 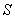 криволинейного треугольника ОАВ может рассматриваться как площадь над кривой ОАВ на отрезке
криволинейного треугольника ОАВ может рассматриваться как площадь над кривой ОАВ на отрезке 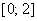 . Однако указанная кривая (ломаная)не задается одним уравнением. Поэтому для нахождения площади необходимо разбить треугольник ОАВ на две части
. Однако указанная кривая (ломаная)не задается одним уравнением. Поэтому для нахождения площади необходимо разбить треугольник ОАВ на две части 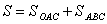 . Координаты точек есть
. Координаты точек есть 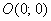 ,
, 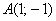 и
и 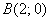 .
.
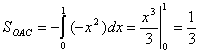 ,
, 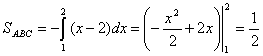 .
.
Окончательно, 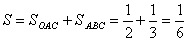 .
.

Билет 19.
Вычисление объемов тел вращения 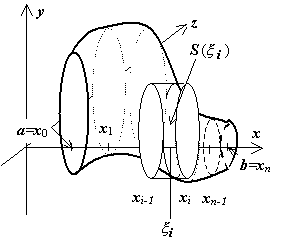

13.4.1. Вычисление объёма тела по площадям поперечных сечений. Пусть тело V расположено в пространстве между плоскостями x = a и x = b, и для 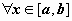 известна площадь его поперечного сечения
известна площадь его поперечного сечения
S = S(x). Требуется определить объём этого тела.
 Рассечём это тело плоскостями x = x0 = a, x = x1, x = x
Рассечём это тело плоскостями x = x0 = a, x = x1, x = x
2, …, x = xi-1, x = xi, …, x = x n-1, x = xn = b на n слоёв (a
= x0< x1 < < x2< …< xn-1 < xn = b), на каждом из
отрезков [xi-1, xi] возьмём произвольную точку 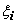 ;
;
будем считать, что объём слоя, заключенного между плоскостями x = xi-1 и x = xi приближённо равен
объёму 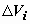 цилиндрика с площадью основания
цилиндрика с площадью основания
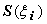 и высотой
и высотой 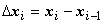 :
: 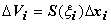 .
.
Сумма объёмов 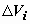 - объём ступенчатой фигуры - при
- объём ступенчатой фигуры - при 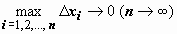 стремится к искомому объёму V, поэтому
стремится к искомому объёму V, поэтому 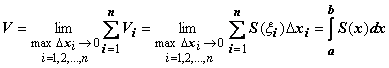 .
.
 13.4.2. Объём тела, получающегося при вращении кривой вокруг координатной
13.4.2. Объём тела, получающегося при вращении кривой вокруг координатной 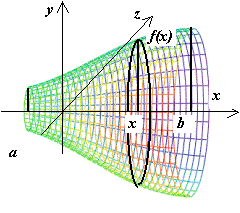 оси. Если объём V получается в результате вращения кривой y = f(x),
оси. Если объём V получается в результате вращения кривой y = f(x), 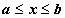 , вокруг оси Ox, то, очевидно,
, вокруг оси Ox, то, очевидно, 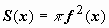 , поэтому
, поэтому 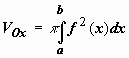 .
.
 Пример: найти объём эллипсоида, получающегося при
Пример: найти объём эллипсоида, получающегося при
вращении эллипса 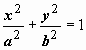 вокруг оси Ox.
вокруг оси Ox.
 Решение: эту задачу проще решить, если применить параметрические уравнения эллипса:
Решение: эту задачу проще решить, если применить параметрические уравнения эллипса: 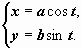 .
.
Верхняя дуга эллипса получается при изменении t от 0 до
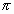 , при этом точке крайней левой точке эллипса соответствует значение параметра t0 , равное
, при этом точке крайней левой точке эллипса соответствует значение параметра t0 , равное 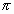 , крайней
, крайней
правой точке соответствует значение tk = 0. Формула 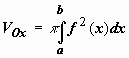 для кривой, заданной параметрически,примет вид
для кривой, заданной параметрически,примет вид 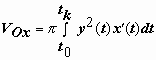 , поэтому
, поэтому 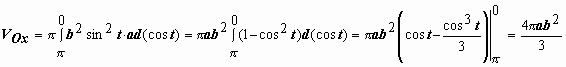 .
.
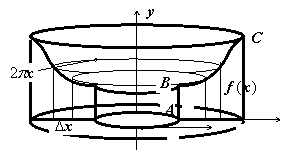
 Если требуется найти объём тела, которой получается при вращении плоской фигуры ABCD вокруг оси Oy, рассуждаем по другому. Разбиваем тело на полые цилиндры радиуса x, толщины
Если требуется найти объём тела, которой получается при вращении плоской фигуры ABCD вокруг оси Oy, рассуждаем по другому. Разбиваем тело на полые цилиндры радиуса x, толщины 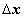 , высоты f(x). Объём этого цилиндра равен произведению длины окружности
, высоты f(x). Объём этого цилиндра равен произведению длины окружности 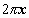 на толщину
на толщину 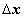 и высоты f(x); суммируя эти объёмы и переходя к пределу при
и высоты f(x); суммируя эти объёмы и переходя к пределу при 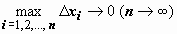 , получим
, получим 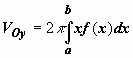 .
.

13.4.3. Объём тела, получающийся при вращении сектора, ограниченного кривой 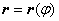 и двумя полярными радиусами
и двумя полярными радиусами 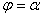 и
и 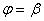 , вокруг полярной осинаходится по формуле
, вокруг полярной осинаходится по формуле 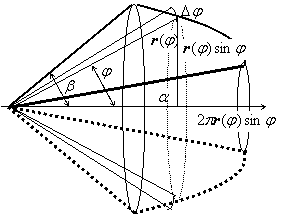
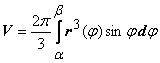 .
.
 Пример: найти объём тора, полученного вращением окружности
Пример: найти объём тора, полученного вращением окружности 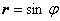 вокруг полярной оси.
вокруг полярной оси.
 Решение:
Решение:
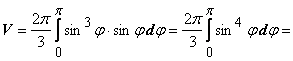
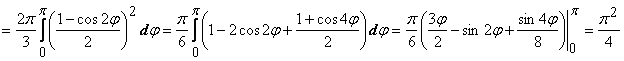 .
.
Билет 20.
