ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ. 1. Найти длину вектора , если
1. Найти длину вектора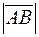 
, если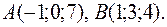 
2. Найти длину вектора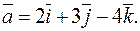 
3. Найти скалярное произведение векторов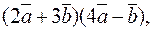 
если 
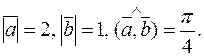
4. Найти скалярное произведение векторов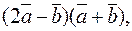 
если
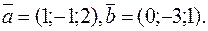
5. Найти косинус угла между векторами 
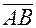и 
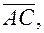если
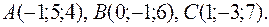
6. Найти косинус угла между векторам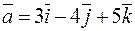и 
и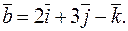 
7. Перпендикулярны ли векторы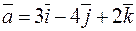 
и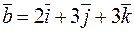 
?
8. При каком значении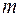 
векторы 
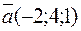и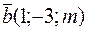 
перпендикулярны?
9. При каком значении 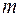векторы 
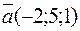и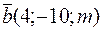 
коллинеарны?
10. Найти векторное произведение векторов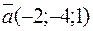 
и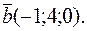 
11. Найти площадь параллелограмма, построенного на векторах
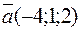и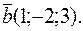 
12. Найтиплощадь параллелограмма, построенного на векторах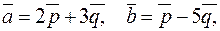 
если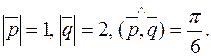 
13. Найти площадь треугольника с вершинами в точках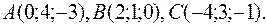 
14. Найти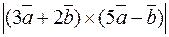 
, если 
, 
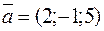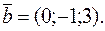
15. Векторы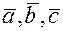 
образуют правую тройку, взаимно перпендикулярны и 
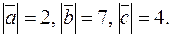Вычислить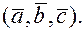 
16. Компланарны ли векторы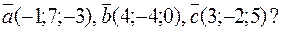 
17. Образуют ли векторы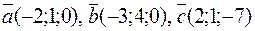 
базис в пространстве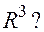 
18. Найти объем тетраэдра, построенного на векторах
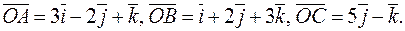
19. Найти объем тетраэдра с вершинами в точках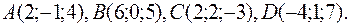 
20. Лежат ли точки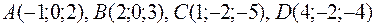
в одной плоскости?
21. Написать уравнение прямой, проходящей через точку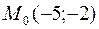 
перпендикулярно вектору нормали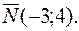 
22. Написать уравнение прямой, проходящей через точку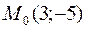 
параллельно направляющему вектору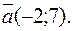 
23. Написать уравнение прямой, отсекающей на осях отрезки длиной 5 и 7 соответственно.
24. Написать уравнение прямой, проходящей через точк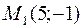и 
и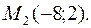 
25. Написать уравнение прямой, проходящей через точку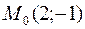 
параллельно прямой 
.
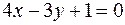26. Написать уравнение прямой, проходящей через точку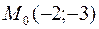 
перпендикулярно прямой 
.
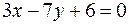27. Написать уравнение прямой, проходящей через точку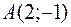 
и составляющей с осью 
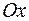угол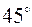 
.
28. Параллельны ли прямые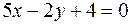
и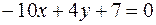 
?
29. Перпендикулярны ли прямые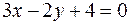
и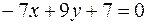 
?
30. Вычислить расстояние от точки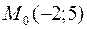 
до прямой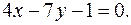 
31. Найти угол между прямым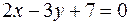и 
и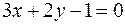 
.
32. Написать уравнение плоскости, проходящей через точку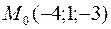 
перпендикулярно вектору нормали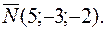 
33. Написать уравнение плоскости, проходящей через три заданные точки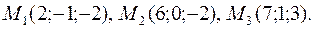 
34. Написать уравнение плоскости, отсекающей на осях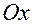 
, 
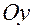и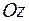 
отрезки длиной 2, 7 и 5 соответственно.
35. Вычислить расстояние от точки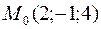 
до плоскости, проходящей через точки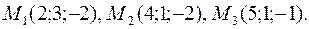 
36. Найти угол между плоскостям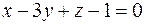и 
и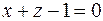 
.
37. Параллельны ли плоскост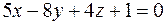и 
и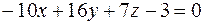 
?
38. Перпендикулярны ли плоскост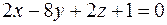и 
и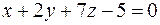 
?
39. Написать уравнение прямой, проходящей через точку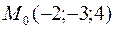 
параллельно вектору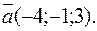 
40. Написать уравнение прямой, проходящей через точки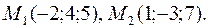 
41. Принадлежит ли плоскости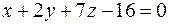 
точка ?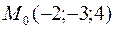
42. Найти эксцентриситет эллипса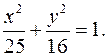 
43. Написать уравнения асимптот гиперболы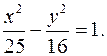 
44. Установить вид кривой второго порядка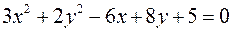 
.
45. Написать каноническое уравнение эллипса, если известно, что расстояние между фокусами равно 6, а малая полуось равна 4.
46. Установить вид кривой второго порядка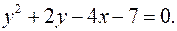 
7. ОТВЕТЫ К ЗАДАЧАМ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
| № задачи | Ответ | № задачи | Ответ |
 |  | ||
 |  | ||
 |  | ||
 | |||
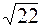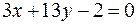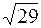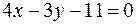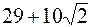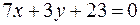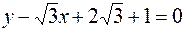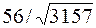 | да | ||
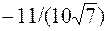 | нет | ||
| да |  | ||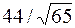
| 90º | |||
| −2 |  | ||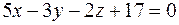
 |  | ||
 |  | ||
 | |||
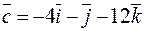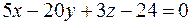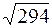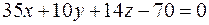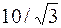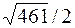 | 90º | ||
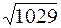 | нет | ||
| да | |||
| нет |  | ||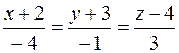
| да |  | ||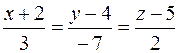
| нет | |||
| 76/3 | 0,6 | ||
| да |  | ||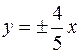
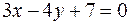 | эллипс с ц. в т. О(1;-2) и полуосями  | ||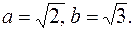
 |  | ||
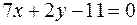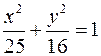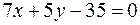 | Парабола с ц. в т.О(-2;-1) и параметром р=2. |
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
[1] Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
[2] Механический смысл скалярного произведения: если вектор изображает силу, точка приложения которой перемещается из начала в конец вектора , то работа указанной силы определяется равенством .