Решение систем нелинейных уравнений установившегося режима методом Зейделя
Суть метода - найденное на текущей (k+1)-й итерации приближение напряжения узла номер (i-1) 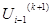 сразу же используется для нахождения (к+1)-го приближения напряжения следующего i-го узла
сразу же используется для нахождения (к+1)-го приближения напряжения следующего i-го узла 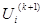 .
.
Нелинейное уравнение установившегося режима в форме баланса токов для i-го узла имеет вид:
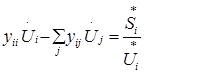 (1)
(1)
Левая часть уравнения – линейна, правая – не линейна. Т.е. уравнение нели-нейно.
Преобразуем это уравнение к виду, удобному для решения итераци-онными методами, т.е. решим его относительно Ui :
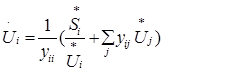 (2)
(2)
Запишем это уравнение в итерационной форме, т.е. с указанием номеров при-ближений:
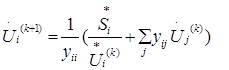 (3)
(3)
Уравнение (3) соответствует вычислительной схеме метода простой итера-ции.
Если при вычислении Ui(к+1) в правую часть выражения (3) подставлять найденные на текущей итерации приближения 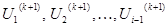 , то получим выражение, соответствующее вычислительной схеме метода Зей-деля:
, то получим выражение, соответствующее вычислительной схеме метода Зей-деля:
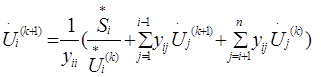 (4)
(4)
Для сети, состоящей из n узлов, нужно записать систему n таких уравне-ний, которая в итерационной форме, соответствующей методу Зейделя, имеет вид:
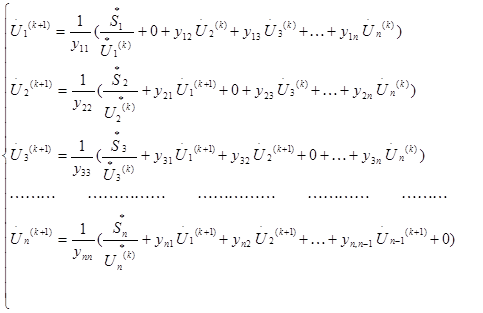 (5)
(5)
Алгоритм решения СНАУ установившегося режима методом
Зейделя
1. Задание условий и параметров расчета:
точность расчета E, предельное количество итераций nпр, счетчик
итераций к=0;
2. Задание начальных приближений неизвестных:
принимаем напряжение U(0)=Uном.
3. Выполнение итерации расчета для всех узлов, кроме опорного, в соот-
ветствии с (5).
При расчете U1(к+1) в правую часть 1-го уравнения подставляем к-е
приближения всех неизвестных. При расчете U2(к+1) в правую часть
2-го уравнения подставляем только что найденное значение U1(к+1) и
к-е приближения остальных неизвестных и т.д. При расчёте послед-
него напряжения Un(к+1) в правую часть последнего уравнения подстав
ляем найденные ранее на этой итерации (к+1)-е приближения осталь-
ных напряжений;
4. Проверка завершения итерационного процесса в соответствии с усло-
вием:
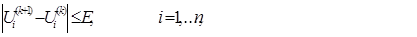 (6)
(6)
Если это условие не выполняется – возврат к п.3. и повторение расчета
при новых приближениях неизвестных.
В модели реальной электрической сети могут присутствовать специ-альные узлы, например, узлы с заданным модулем напряжения (узлы с фик-сацией модуля напряжения ФМ). В таких узлах заданными параметрами яв-ляются Uз (модуль напряжения) и Pз (активная мощность). Искомыми явля-ются 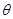 (угол напряжения) и Q (реактивная мощность), либо вместо
(угол напряжения) и Q (реактивная мощность), либо вместо 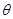 могут быть составляющие напряжения -
могут быть составляющие напряжения - 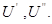
Для обеспечения фиксации модуля напряжения в ходе расчета можно выполнить следующее: переводим на каждом шаге итерационного процесса, узлы ФМ в состав нагрузочных узлов с использованием уравнений устано-вившегося режима, записанных для Q:
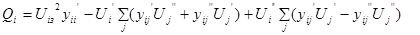 (7)
(7)
где Uiз -заданный модуль напряжения в i-ом узле,
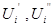 - искомые составляющие напряжения в i-ом узле.
- искомые составляющие напряжения в i-ом узле.
При этом должно выполняться условие:
 (8)
(8)
Для того чтобы это условие выполнялось на каждом шаге итерационно-го процесса, составляющие напряжения корректируют в соответствии со следующими формулами:
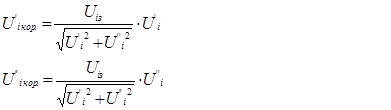 (9)
(9)
Итерационный процесс заканчивается, когда выполняется условие (6) для всех узлов:

Более точным и надежным критерием завершения итерационного про-цесса является анализ невязок уравнений.
Сходимость метода Зейделя
Анализируя сходимость итерационного метода – рассматриваем, прежде всего, скорость сходимости (необходимое количество итераций) и характер сходимости (колебательная или экспоненциальная).
Экспериментально выявлен ряд факторов, влияющих на скорость сходи-мости. Сходимость улучшается при:
1) более точном задании начальных приближений по напряжению;
1)2) разгрузке сильно загруженных линий;
1)3) увеличении числа генерирующих узлов с заданным модулем напря-жения (узлы ФМ) и широким диапазоном изменения реактивной мощности;
1)4) увеличение числа контуров в сети;
1)5) увеличение числа связей БП с остальными узлами;
Т.е. улучшение режима работы электрической сети – разгрузка ЛЭП, повы-шение уровней напряжений и т.д. – улучшает сходимость итерационного процесса. И наоборот – утяжеление режима, приводит к ухудшению сходи-мости и развалу итерационного процесса. Т.о. рассчитываемый режим рабо-ты электрической сети влияет на характеристики итерационного процесса.
Сходимость метода Зейделя для СНАУ установившегося режима до-вольно медленная (для сети 100-200 узлов требуется около 300-500 итера-ций).
Сходимость может быть улучшена с помощью коэффициентов ускоре-ния (метод неполной релаксации).
Пусть 
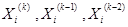 - значения переменной x на
- значения переменной x на 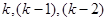 итерациях. Тогда (к+1 )- е приближение можно определить по формуле:
итерациях. Тогда (к+1 )- е приближение можно определить по формуле:
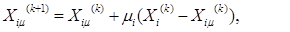 (10)
(10)
где 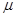 -коэффициент ускорения;
-коэффициент ускорения;
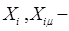 приближения, вычисленные без учета
приближения, вычисленные без учета 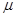 и с учетом
и с учетом 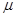 .
.
При 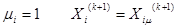 .
.
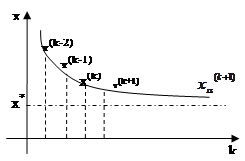
Значения коэффициента 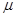 выбирается в зависимости от характера сходимости итерационного процесса. Если сходимость монотонная, то:
выбирается в зависимости от характера сходимости итерационного процесса. Если сходимость монотонная, то:
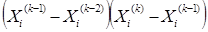 >0 (11)
>0 (11)
Если сходимость монотонная, то принимают 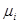 >1. Использование ускоряющего коэффициента
>1. Использование ускоряющего коэффициента 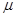 на каждой итерации позволяет приблизить очередное значение к точному решению. Этим ускоряется сходимость.
на каждой итерации позволяет приблизить очередное значение к точному решению. Этим ускоряется сходимость. 

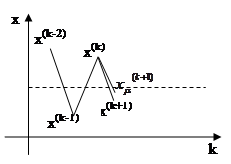 Если характер сходимости колебательный, то выражение (11) будет меньше нуля и значение коэффициента принимают
Если характер сходимости колебательный, то выражение (11) будет меньше нуля и значение коэффициента принимают 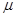 <1 .
<1 .
В этом случае коэффициент является демпфирующим – он позволяет уменьшить ам-плитуду отклонений приближений и умень-шить количество итераций.
Возможные причины отказа сходимости итерационного процесса
1. Не правильное задание исходных данных (параметры схемы, задан-ные параметры режима)
2. Заданные значения нагрузок и генерации превышает пропускную спо-собность элементов сети, либо всей сети в целом.
Для того, чтобы убедиться, что итерационный процесс расходится из-за ошибок в исходных данных, нужно провести инженерный анализ соотноше-ний сопротивлений и нагрузок, значений напряжений.
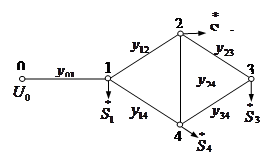
Пример:
Для заданной схемы записать систе-му уравнений установившегося режима (баланс токов) в форме, обеспечивающей решение её методом Зейделя.
Запишем для заданной схемы уравне-ния установившегося режима в форме ба-ланса токов вида:
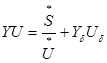 :
:
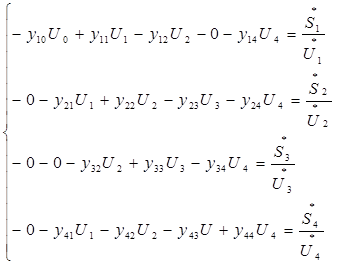
Так как балансирующий узел (0) связан только с 1-й узлом, то перено-сим соответствующий элемент 1-го уравнения в правую часть:
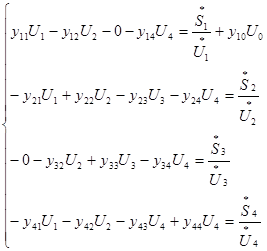
Данную систему преобразовываем в соответствии с формулой (5), т.е. решаем каждое уравнение относительно одной из неизвестных и записываем в итерационной форме в соответствии алгоритмом метода Зейделя: