Производные высших порядков. Если функция у=ƒ(х) имеет производную ƒ¢(х), которая, вообще говоря, сама является дифференцируемой функцией

Если функция у=ƒ(х) имеет производную ƒ¢(х), которая, вообще говоря, сама является дифференцируемой функцией, то производная от ƒ¢(х) называется производной второго порядка (или второй производной) от функции ƒ(х) и обозначается: у^и, ƒ¢¢(х), т. е.

ƒ¢¢(х)=(ƒ¢(х))¢.

Аналогично, производной третьего порядка (третьей производной) от функции ƒ(х) называется производная от второй производной ƒ¢¢(х), т. е.

ƒ¢¢¢(х)=(ƒ¢¢(х))¢.

Производная четвертого порядка

ƒ^IV(х)=(ƒ¢¢¢(х))¢.

Например, для функции

ƒ(х)=2х⁶–sin3x

ƒ¢(x)=12x⁵–3cos3x,

ƒ¢¢(x)=12·5x⁴–3·(–sin3x)·3=60x⁴+9sin3x,

ƒ¢¢¢(x)=60·4x³+9·cos3x·3=240x³+27cos3x,

ƒ^IV(x)=240·3x²–27sin3x·3=720x²–81sin3x и т. д.

Производную порядка n обозначают:

y⁽ⁿ⁾ или ƒ⁽ⁿ⁾(x).

Приложения дифференциального исчисления

Были рассмотрены некоторые приложения производной, а именно: задача о касательной к графику функции, отыскание интервалов монотонности функции. С помощью производных вычисляются пределы, приводящие к неопределенностям 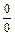и .

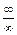Правило Лопиталя.

Теорема.Предел отношения двух бесконечно малых или двух бесконечно

больших функций равен пределу отношения их производных.

Заметим, что речь идет о дифференцируемых функциях, во-первых, и во-вторых, предел отношения производных вычисляется при том же условии, что и данный предел.

Итак, 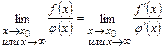, ес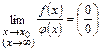ли

или =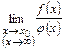

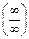
Пример 1.

Найти следующие пределы

1)

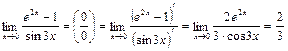
2) 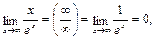т. к. 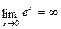, 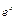– бесконечно большая при х®∞

3)

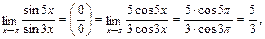
т. к. cos 5π=cos(4π+π)=cos π= –1.

cos 3π=cos(2π+π)=cos π= –1.

Рассмотрим случай неоднократного применения правила Лопиталя.

4) .

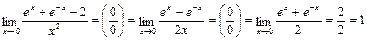Правило Лопиталя было применено дважды.

Рассмотрим случай, когда правило Лопиталя не приводит к желаемому результату.

5)

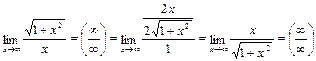
Применение правила Лопиталя не позволяет раскрыть эту неопределенность, но предел этот легко вычисляется, если числитель и знаменатель дроби одновременно разделить на х

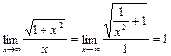, т.к. .

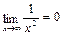Правило Лопиталя помогает раскрыть неопределенности вида 0·∞, ∞–∞.

6)

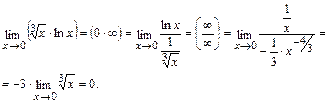
7) ,

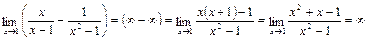т. к.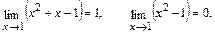

Экстремум функции

Исследование функции на экстремум – одно из важнейших приложений производных. Рассмотрим определение минимумов и максимумов, и способы их отыскания.

Пусть функция ƒ(х) определена и дифференцируема на некотором множестве и точка х₀ – точка внутри него.

Определение. Функция ƒ(х) в точке х₀ имеет максимум (минимум), если

существует такая окрестность точки х₀, что для всех х из

этой окрестности

ƒ(х) < ƒ(х₀) (ƒ(х) > ƒ(х₀)).

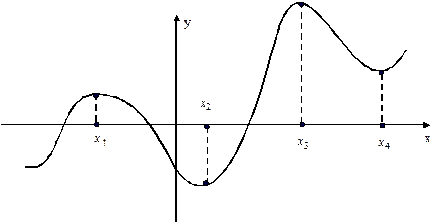Точка х₀ называется тогда точкой максимума (минимума).

Рис. 25.

Показан график функции, которая имеет две точки максимума (х₁ и х₃) и две точки минимума (х₂ и х₄), причем максимальное значение может оказаться меньше минимального (ƒ(х₁) < ƒ(х₄)). Это подчеркивает тот факт, что мы характеризуем особенность функции только вблизи некоторой точки.

Значения функции в точках максимума и минимума называют экстремальными значениями или экстремумами. На приведенном графике видно, что точки экстремума (х₁, х₂, х₃, х₄) определяют интервалы монотонности функции, в каждом из которых производная сохраняет определенный знак. В точках экстремума, понятно, производная обращается в нуль. Сформулируем теорему о необходимом условии существования экстремума.

Теорема.Если функция ƒ(х) в точке х₀ имеет экстремум, то производная

функции в этой точке равна нулю, т. е. ƒ¢(х₀)=0.

Заметим сразу, что условие это не является достаточным, т. е. обратное утверждение не всегда верно. Из равенства ƒ¢(х₀)=0 не обязательно следует, что в точке х₀ существует экстремум.

Подтверждением тому пример с функцией ƒ(х)=х³.

Найдем ƒ¢(х)=3х². В точке х=0 ƒ¢(0)=0. Но как угодно близко к точке х=0 найдем х>0, где ƒ(х)=х³ > 0, найдем х<0, где ¦(х)=х³<0. Т. е. не существует какая-либо малая окрестность точки х=0, где для всех х значение функции в точке х=0 будет самым большим или самым малым. Поэтому точка х=0 не является точкой экстремума.

Можно рассуждать иначе. Так как производная ƒ¢(х)=3х², то функция ƒ(х)=х³ возрастает при любых действительных х и экстремумов не имеет.

Точки, в которых выполняется необходимое условие экстремума (ƒ¢(х)=0) называются критическими.

Очевидно, что касательная к графику функции в точках, где ƒ¢(х)=0, параллельна оси абсцисс Ох.

Достаточное условие экстремума дается в следующих теоремах.

Теорема 1. Если х₀ – критическая точка функции и при переходе через

нее производная меняет знак, то х₀ – точка экстремума, а

именно, если производная меняет знак с плюса на

минус – точка максимума, если – с минуса на плюс – точка

минимума.

Заметим, что экстремума в точке нет, если производная не меняет знака. Правило исследования на экстремум с помощью первой производной известно из школьного курса. Достаточное условие экстремума иногда удобнее формулировать с помощью второй производной.

Пусть функция ƒ(х) дважды дифференцируема в некоторой области (т. е. ƒ(х)имеет ƒ¢(х) и ƒ¢¢(х)).

Теорема 2.Если х₀ – критическая точка функции ƒ(х) и ƒ¢¢(х₀) > 0, то

х₀ – точка минимума, если ƒ¢¢(х₀) < 0, то х₀ – точка максимума.

С помощью второй производной определяется выпуклость или вогнутость графика функции.