Выводы по второй главе

В концепции модернизации образования приоритетной целью призвана развивающая. Рассматривая развивающие возможности математики, в большей степени говорят о развитии логического и алгоритмического мышления. Алгоритмическое мышление является необходимой частью научного взгляда на мир. В то же время оно включает и некоторые общие мыслительные навыки, полезные и в более широком контексте. К таким относится, например, разбиение задачи на подзадачи. Алгоритмическое мышление на уроках математики развивается при помощью различных задач и заданий направленных на развитие логики.

Алгоритмический подход к решению наблюдается во многих видах задач. Большинство предлагаемых из них в начальной школе имеет алгоритмическую структуру. С целью выявления способа действий полезны комбинаторные задачи. Учащимся доступны следующие способы описания алгоритмов: развернутое словесное описание; таблица; граф – схемы; блок – схемы. Составление алгоритмического предписания или алгоритма – сложная задача, поэтому начальный курс математики не ставит своей целью её решение. Но определённую подготовку к её достижению он берёт на себя, способствуя тем самым развитию алгоритмического мышления школьников. Для этого, начиная с 1-ого класса, нужно, прежде всего, учить детей «видеть» алгоритмы и осознавать алгоритмическую сущность тех действий, которые они выполняют. Начинать эту работу следует с простейших алгоритмов, доступных и понятных им.

Алгоритм в начальных классах описывают последовательность действий на конкретном примере не в общем виде, в них находят не все операции, входящие в состав выполняемых действий, поэтому их последовательность строго не определена.

ЗАКЛЮЧЕНИЕ

Изучая состояние исследуемой проблемы в психолого-педагогической и учебно-методической литературе, мы пришли к следующим выводам.

1. Проблема формирования и развития логического и алгоритмического мышления учащихся является одной из основных психолого-педагогических проблем. Ей посвящены многие исследования отечественных и зарубежных педагогов, психологов, методистов. Именно на труды этих авторов мы опирались в раскрытии темы курсовой работы.

Мышление ребенка в той или иной мере развивает каждый учебный предмет, преподаваемый в начальной школе. Однако математика среди других предметов занимает особое место. Именно на этих уроках уместна постановка и решение педагогической задачи – формирование логического и алгоритмического стиля мышления.

2. В работе нами раскрыта сущность таких понятий, как: “мышление”, “алгоритм”, “алгоритмическое мышление”. Таким образом, мышление — это обобщенное отражение объективной действительности в ее закономерных, наиболее существенных связях и отношениях. Алгоритмическое мышление — это система мыслительных приёмов направленных на решение задач. Иногда психологи называют его алгоритмический стиль мышления.

Такой тип мышления очень сильно помогает освоению многих знаний и навыков, в том числе и школьных предметов. Под способностью алгоритмически мыслить понимается умение решать задачи различного происхождения, требующие составления плана действий для достижения желаемого результата.

3. Рассмотрели также особенности развития алгоритмического мышления младших школьников, развитие которого в системе начального образования является необходимой составляющей. Важнейшей задачей работы по развитию мыслительной деятельности является вооружение учеников общими приемами мышления. Алгоритм является одним из видов общих методов мыслительной деятельности. Поэтому применение алгоритмического метода и формирование у учащихся алгоритмического мышления становится актуальной темой сегодняшнего дня.

4. Возможности использования элементов алгоритмизации на уроках математики в начальной школе с целью развития алгоритмического мышления школьников являлся одним из вопросов курсовой работы. Мы показали, что знакомство младших школьников с алгоритмами не требует специального времени на уроках математики. Это можно сделать в процессе решения задач, уравнений, неравенств и нахождения значений различных выражений. Деятельность учащихся в процессе решения многочисленных примеров, которые предлагаются на каждом уроке математики, не отличается разнообразием. Поэтому решение примеров в виде блок-схем, алгоритмов значительно оживляет урок, вносит элементы занимательности. Главной целью использования алгоритмов на уроках математики является развитие алгоритмического, конструктивного, логического мышления учеников. Навыки алгоритмического мышления способствуют формированию особого стиля культуры человека, составляющими которого являются: целеустремленность и сосредоточенность, объективность и точность, логичность и последовательность в планировании и выполнении своих действий, умение четко и лаконично выражать свои мысли.

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Алгоритм. Свойства алгоритма. [Электронный ресурс]– Режим доступа к статье: http://www.gym075.edusite.ru – (Дата обращения: 15.11.2014).

2. Блонский, П.П. Педология. / П.П. Блонский – М.: ВЛАДОС, 2000. – 288 с.

3. Богословский, В.В. Общая психология. : учеб. пособие для студентов пед. ин-тов. / В.В. Богословский, А.А. Степанов, А.Д. Виноградова; под ред. В. В. Богословского и др. – 3-е изд., перераб. и доп. — М.: Просвещение, 1981. — 383 с. : ил.

4. Дарвиш, О.Б. Возрастная психология. : учеб. пособие для высш. учеб. заведений / О.Б. Дарвиш; под ред. В.Е. Клочко. – М.: Владос-пресс, 2003. –264 с.: ил.

5. Доморяд, А.П. Математические игры и развлечения. / А.П. Доморяд – М.: ГИФМЛ, 1961. – 68 с.

6. Зак, А.З. Развитие теоретического мышления у младших школьников. / А.З. Зак – М.: Наука, 1984. – 220с.

7. Илъенков, Э.В. Диалектическая логика. / Э.В. Илъенков – 2-е изд., доп. – М., 1984. – 320 с.

8. Информатика и ИКТ. Учебник для 9 класса. / И.Г. Семакин, Л.А.Залогова [и др.] – 5-е изд. – М., 2012 – 341с.

9. Информатика. 7-9 кл. Базовый курс. Практикум-задачник по моделированию. / Н.В. Макарова, Г.С. Николайчук, Ю.Ф. Титова [и др.]; под ред. проф. Н.В. Макаровой. – СПб.: Питер, 2007. – 176 с.

10. Истомина, Н.Б. Методика бучения математике в начальных классах. : учеб. пособие для студ. сред. и высш. пед. учеб.заведений. / Н.Б.Истомина – 5-е изд. – М.: Академия, 2002. – 288 с.

11. Козлова, Е.Г. О возможностях формирования у младших школьников способности к работе с алгоритмизированными обучающими средствами / Е.Г.Козлова // Начальная школа. – 2004. – № 2. – С.99-112.

12. Константинов, В.В. Основы общей психологии: мышление. память, внимание. : учебно-методическое пособие. / В.В. Константинов – Пенза: Пензенский государственный педагогический университет им. В.Г. Белинского, 2005. – 76 с.

13. Леонтьев, А. Н. Избранные психологические произведения: В 2-х т. Т. I / А. Н. Леонтьев – М.: Педагогика, 1983. – 392 с.: ил. – (Труды д. чл. и чл.-кор. АПН СССР).

14. Новоселова, С.Л. Развитие мышления в раннем возрасте. / С.Л.Новоселова – М., 1978.

15. Маклаков, А.Г. Общая психология. / А.Г. Маклаков – СПб: Питер, 2001. – 592с.

16. Младший школьник: развитие познавательных способностей / И.В.Дубровина, А.Д. Андреева, Е.Е. Данилова [и др.]; под ред. И.В. Дубровиной. – М.: Просвещение, 2003. – 148 с.

17. Моро, М.И. Математика. 1 класс. : Учебник. Части 1-2. / М.И. Моро, С.И. Волкова, С.В Степанова – 6-е изд. – М.: Просвещение, 2006. –Ч.1– 112 с.

18. Моро, М.И. Математика. 2 класс. : Учебник. Части 1-2. / М.И. Моро [и др.] – М.: 2012. –Ч.1 – 96с., Ч.2 – 112с.

19. Моро, М.И. Математика. 3 класс. : Учебник. Части 1-2. / М.И. Моро, М.А. Бантова [и др.] – М.: 2012. – Ч.1 – 96с., Ч.2 – 112с.

20. Моро, М.И. Математика. 4 класс. : Учебник. Части 1-2. / М.И. Моро, М.А. Бантова [и др.] – М.: 2011. –Ч.1 – 112 с., Ч.2 - 112с.

21. Острейковский, В.А. Информатика. Теория и практика. / В.А. Острейковский, И.В. Полякова – М., 2008. – 608 с.

22. Побединская, И.В. Развитие алгоритмического мышления и творческих способностей учащихся в начальном звене // Начальная школа. – 2000. – № 4. – С.110-116.

23. Подготовка к олимпиадам как средство формирования познавательного интереса к математике у младших школьников. [Электронный ресурс] / Е.А.Смирнова – 2014 – Режим доступа к статье: http://nsportal.ru– (Дата обращения: 26.12.2014).

24. Рабочая книга школьного психолога / И.В. Дубровина, М.К. Акимова, Е.М. Борисова [и др.]; под ред. И.В. Дубровиной. – М.: Международная педагогическая академия, 1995.

25. Развитие логико-алгоритмического мышления у младших школьников на уроках математики [Электронный ресурс] – 2009. – Режим доступа к статье: http://edu-reforma.ru – (Дата обращения: 17.02.2015).

26. Реан, А.А. Психология и педагогика. / А.А. Реан, Н.В. Бордовская, С.И.Розум – СПб.: Питер, 2010. – 432 с.: ил. – ( Серия “Учебное пособие”).

27. Рубинштейн, С.Л. Основы общей психологии. / С.Л. Рубинштейн – СПб: Питер, 2000. – 520 с.

28. Стойлова, Л.П. Математика. / Л.П. Стойлова – М., 2002. – 424 с.

29. Стили мышления и обучение программированию студентов педагогического вуза [Электронный ресурс] / А. И. Газейкина – 2006. – Режим доступа к статье: http://ito.edu.ru – (Дата обращения: 15.01.2015).

30. Талызина, Н.Ф. Управление процессом усвоения знаний. / Н.Ф. Талызина – 2-е изд., доп. – М.: МГУ, 1984.

31. Теплов, Б.М. Практическое мышление / Б.М. Теплов // Хрестоматия по общей психологии: Психология мышления. – М.: МГУ, 1981.

32. Тихомирова, Л.Ф. Формирование и развитие интеллектуальных способностей ребенка. Младшие школьники. / Л.Ф. Тихомирова – М.: Рольф, 2000.

33. Туревская Е.И. Возрастная психология / Е.И. Туревская. – Тула.: Изд-во Тульского государственного педагогического университета им. Л.Н.Толстого, 2002. – 32 с.

34. Угринович Н.Д. Информатика и информационные технологии. Учебник для 10-11 классов. / Н.Д. Угринович – М., 2003. – 512 с.

35. Уроки математики в начальной школе – развитие мышления у детей на уроках математики [Электронный ресурс] – 2014. – Режим доступа к статье: http://lifeshen.biz – (Дата обращения: 15.03.2015).

36. Формирование алгоритмического мышления у школьников в ходе групповой работы. / Н.Н. Еремеева // Пермский педагогический журнал – 2013.– №4 – С. 25–29.

37. Шимина А.Н. Логико-психологичесие основы процесса формирования понятий в обучении. / А.Н. Шимина – М., 1981.

38. Штейнмец А.Э. Общая психология. : учеб. пособие для студ. высш. учеб. заведений. / А.Э. Штейнмец – М.: Академия, 2006. – 288 с.

ПРИЛОЖЕНИЯ

Приложение А

Структурная схема алгоритма

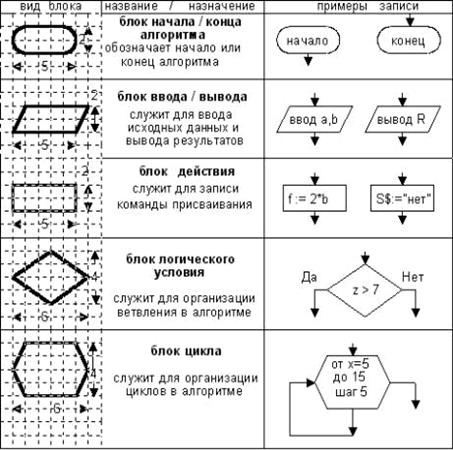
Приложение Б