Интерполяционный многочлен Лагранжа 2 страница
Следовательно разложение имеет вид
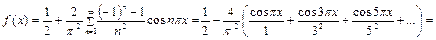
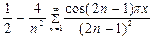 .
.
Порядок выполнения работы
1. Разложить в ряд Фурье функцию f(х)=х, заданную в промежутке 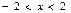 .
.
2. Разложить в ряд Фурье периодическую функцию f(х) =│x│, на отрезке 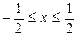 .
.
3. Разложите в ряд Фурье только по синусам функцию 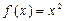 , заданную в промежутке
, заданную в промежутке 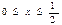 .
.
4. 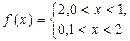 .
.
5. 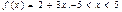
6. 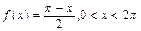
7. 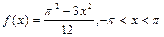
8. 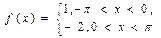
Ответы: 1) 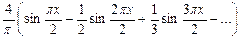 .
.
2) 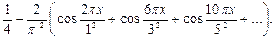
3) 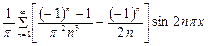 .
.
4) 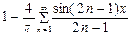
5) 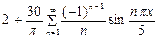
6) 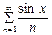
7) 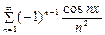
8) 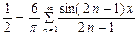
Контрольные вопросы
1. Функция 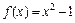 разложена в ряд Фурье по синусам на отрезке [0; 1]. Чему равна сумма ряда в точках
разложена в ряд Фурье по синусам на отрезке [0; 1]. Чему равна сумма ряда в точках 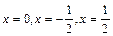 ? Чему равен период суммы ряда?
? Чему равен период суммы ряда?
Практическая работа № 4
Тема «Разложение в ряд Фурье непериодических функций»
Основные вопросы: Представление непериодической функции в ряд Фурье на любом конечном промежутке. Понятие суммы ряда во всех точках отрезка, в точке разрыва. Доопределение функции на отрезке, получение периодической функции( четным и нечетным образом).
Краткие теоретические сведения: Пусть функция f(x) задана на отрезке [a; b], причем функции f(x), 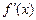 непрерывны на [a; b] или имеют на этом отрезке конечное число точек разрыва первого рода. Покажем, что заданную функцию f(x) в точках ее непрерывности можно представить в виде суммы ряда Фурье.
непрерывны на [a; b] или имеют на этом отрезке конечное число точек разрыва первого рода. Покажем, что заданную функцию f(x) в точках ее непрерывности можно представить в виде суммы ряда Фурье.
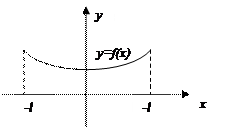 |
Рисунок 7
Для этого рассмотрим функцию f1(x) с периодом 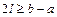 , совпадающую с функцией f(x) на отрезке [a; b]. Разложим функцию f1(x) в ряд Фурье
, совпадающую с функцией f(x) на отрезке [a; b]. Разложим функцию f1(x) в ряд Фурье
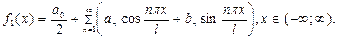
Если 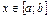 , то f1(x)= f(x), следовательно,
, то f1(x)= f(x), следовательно,
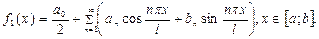 .
.
Это и есть разложение в ряд Фурье функции f(x), заданной на отрезке [a; b].
Рассмотрим два частных случая.
1. Пусть функция f(x) задана на отрезке [0; l] . Доопределим так, чтобы при 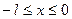 было f(x)= f(-x), в результате получится четная функция
было f(x)= f(-x), в результате получится четная функция
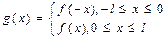 .
.
В этом случае говорят, что функция f(x) продолжена четным образом
Разложим функцию g(x) на отрезке [-l; l] в ряд Фурье
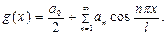
где 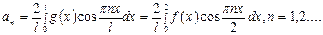
Коэффициенты 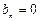 , так как g(х) – четная функция.
, так как g(х) – четная функция.
Если 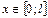 , то g(x) и f(x), следовательно,
, то g(x) и f(x), следовательно,
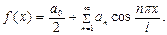
2. Аналогично, продолжая f(x) нечетным образом, получим нечетную функцию
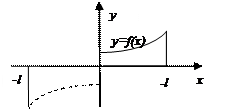
Рисунок 8
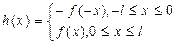 ,
,
которая разлагается в ряд Фурье по синусам.
На отрезке [0; l] 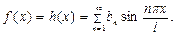
где 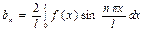 .
.
Таким образом, функцию f(x), заданную на отрезке [0; l], можно разложить в ряд Фурье как по косинусам, так и по синусам.
Примеры решения задач
Пример 1. Пусть требуется разложить функцию f(x)= x на отрезке [0; 1] в ряд по косинусам.
Решение. Продолжим эту функцию четным образом, получим 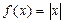 ,
, 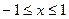 . Разлагая ее в ряд, найдем
. Разлагая ее в ряд, найдем
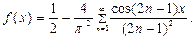
При 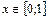 будем иметь
будем иметь
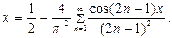
Пример 2. Разложить функцию f(x)= x на отрезке [0; 1] в ряд Фурье по синусам.
Решение. Искомое разложение имеет вид 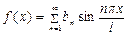 ,
,
где 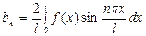 . Так как l=1, а f(x)= x
. Так как l=1, а f(x)= x 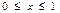 , то
, то
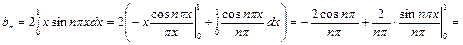
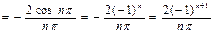 .
.
следовательно, 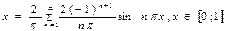
Пример 3. Разложить в ряд Фурье 2l-периодическую функцию 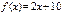 , на
, на 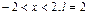 .Построить график суммы ряда.
.Построить график суммы ряда.
Решение. Для вычисления коэффициентов Фурье воспользуемся формулами
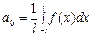 ,
, 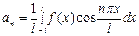 ,
, 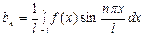 , n=0, 1, 2, … .
, n=0, 1, 2, … .
Имеем: 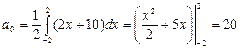 .
.
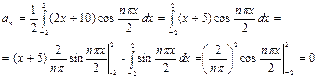
n=0, 1, 2, 3, … .
Аналогично находим
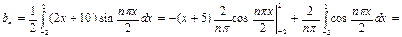
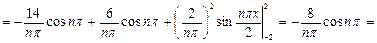
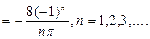
Подставляя найденные коэффициенты в формулу, получаем разложение функции f(x) в ряд Фурье: 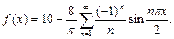
Построим график суммы ряда. Сумма ряда S(x)имеем период Т=2l=4 и S(x)=f(x), т. е. для всех 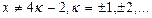
Если 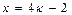 ,
, 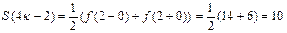
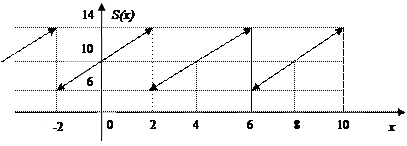
Рисунок 9
Порядок выполнения работы
- Разложите в ряд Фурье периодическую функцию, заданную в промежутке
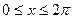 :
:
а) 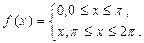 б)
б) 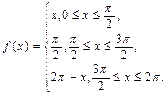
в) 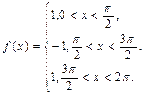 г)
г) 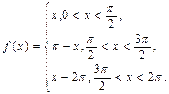
Ответ: а) 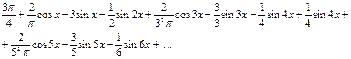 .
.
б) 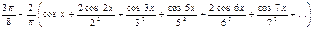 .
.
в) 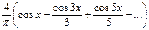 .
.
г) 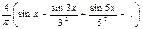 .
.
Контрольные вопросы
1. Сформулируйте правила разложения функций в ряд Фурье, заданных на промежутке [0; 2l].
Практическая работа № 5
Тема: «Комплексная форма рядов Фурье»
Основные вопросы: Разложение периодических кривых геометрически правильной формы и кривых произвольной (геометрически правильной) формы.
Краткие теоретические сведения: Пусть функция f (x) определена 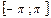 . Применяя формулы Эйлера
. Применяя формулы Эйлера 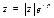 ,
, 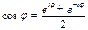 ,
, 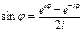 .
.
Можно записать в ряд Фурье данной функции в комплексной форме:
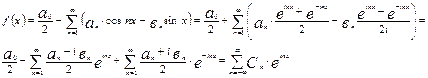
Мы использовали здесь следующие обозначения
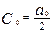 ,
, 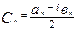 ,
, 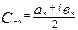 .
.
Коэффициенты Сn называется комплексными коэффициентами Фурье.
Они определяются формулами
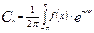
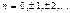
Если нужно построить продолжение функции f(x),имеющей произвольный период 2L,то соответствующее выражение в комплексной форме имеет вид
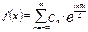 где,
где, 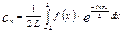 ,
, 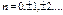
Комплексная форма ряда Фурье алгебраически проще и более симметрична. Поэтому, она часто используется в физике и прикладных расчетах.
Примеры решения задач
Пример 1. Используя комплексную форму записи, найти разложение в ряд Фурье функции. 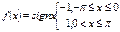
Решение: Вычислим коэффициент С0 и Сn ( 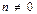 ).
).
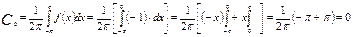
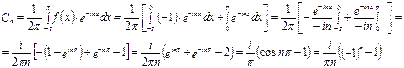
Если n=2k, то С2k=0
Если n= 2k-1, то
Следовательно, разложение в ряд Фурье в комплексной форме имеет вид:
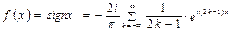
Данный ряд можно преобразовать и записать в действительных переменных. Обозначим:
n = 2k-1, тогда
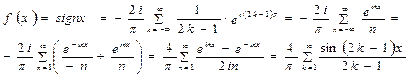
Контрольные вопросы
1. Выведите формулы для коэффициентов Фурье для функции комплексного переменного.
Практическая работа № 6
Тема: «Разложение функций в ряд Фурье
для анализа несинусоидальных напряжений и токов»
Основные вопросы: Разложение периодических кривых геометрически правильной формы и кривых произвольной (геометрически правильной) формы.
Краткие теоретические сведения: При изучении различных зависимостей в электических цепях с несинусоидальными токами применяют ряды Фурье. Переменный синосоидальный ток 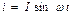 имеет период
имеет период 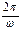 . Несинусоидальный ток разлагают в ряд Фурье вида
. Несинусоидальный ток разлагают в ряд Фурье вида
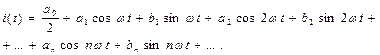 (9)
(9)
Формулы для нахождения коэффициентов ряда (9) получаются из формул:
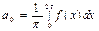 ,
, 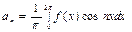 ,
, 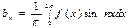 ,
,
с помощью замены переменной 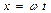 и имеют вид:
и имеют вид:
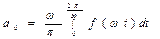 ,
, 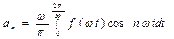 ,
, 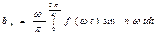 . (10)
. (10)
Примеры решения задач
Пример 1. Разложить в ряд Фурье функцию двухполупериодного выпрямленного синусоидального тока:
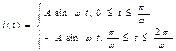 .
.
Решение: 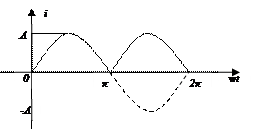
Рисунок 10
Данная функция является четной, поэтому 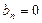 . По формулам (2) находим
. По формулам (2) находим 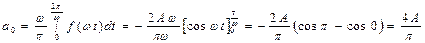
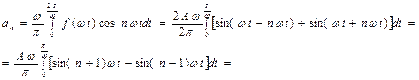
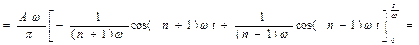
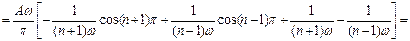
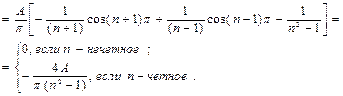
Тогда 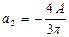 ,
, 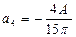 ,
, 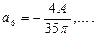
Подставляя эти значения в (1), получим
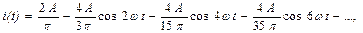
или 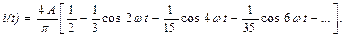
Пример 2. Разложить в ряд Фурье функцию
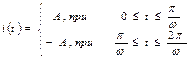
Решение. Выполним рисунок функции
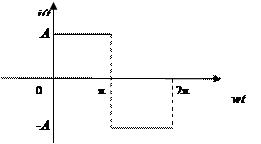
Рисунок 11
Данная функция является нечетной, поэтому 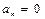 . По формулам (2) находим
. По формулам (2) находим
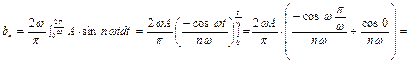
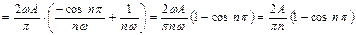
при 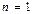
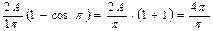 ,
,
при 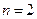
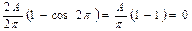 ,
,
при 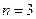
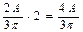 ,
,
при 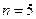
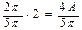 .
.
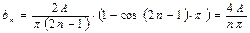
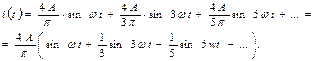
Пример 3. Разложите в ряд Фурье функцию 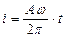 .
.
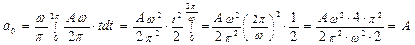
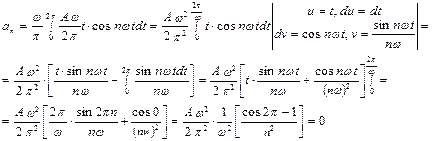
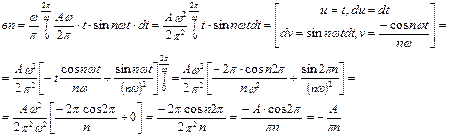
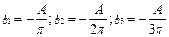
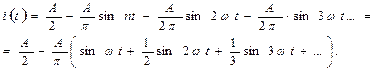
Порядок выполнения работы
1. Разложите в ряд Фурье функцию однополупериодного выпрямленного синусоидального тока (рисунок 12 ).
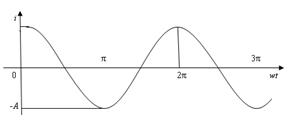
Рисунок 12
2. Разложите в ряд Фурье функцию двухполупериодного выпрямленного синусоидального тока (рисунок 13).
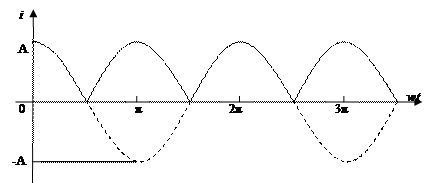
Рисунок 13
Ответы: 1) 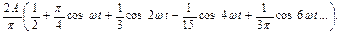
2) 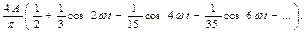
Контрольные вопросы
1. Каковы основные свойства функций, образующих основную тригонометрическую систему?
2. Можно ли функцию 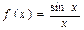 разложить в ряд Фурье на отрезке
разложить в ряд Фурье на отрезке 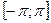 .
.
3. Функция 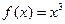 разложена в ряд Фурье на отрезке
разложена в ряд Фурье на отрезке 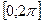 . Чему равна сумма ряда в точках х = 0, х = –π?
. Чему равна сумма ряда в точках х = 0, х = –π?
4. По каким функциям разлагается в ряд Фурье четная (нечетная) функция?
5. Функция 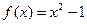 разложена в ряд Фурье по синусам на отрезке
разложена в ряд Фурье по синусам на отрезке 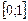 . Чему равна сумма ряда в точках
. Чему равна сумма ряда в точках 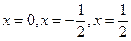 ? Чему равен период суммы ряда?
? Чему равен период суммы ряда?
6. Сформулируйте определение ряда и коэффициентов Фурье.
7. Сформулируйте теорему о сходимости ряда Фурье.
8. Запишите разложение функции с произвольным периодом в ряд Фурье.
Практическая работа № 7
Тема: «Погрешности приближенных значений чисел»
Основные вопросы: Абсолютная и относительные погрешности. Значащие и верные цифры. Действия над приближенными цифрами.
Краткие теоретические сведения:
Определение 1: Модуль разности между точным значением х и его приближенным значением а называется абсолютной погрешностью приближенного значения х и обозначается 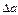 :
:
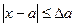 ,
, 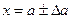 .
.
Пример 1. Даны приближенные значения числа 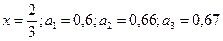 . Какое из этих трех приближений является лучшим?
. Какое из этих трех приближений является лучшим?
Решение. Найдем абсолютную погрешность каждого числа
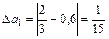 ;
; 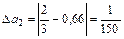 ;
; 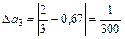 .
.
Лучшим приближением числа х является 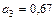 .
.
Определение 2. Цифра m приближенного числа а называется верной в широком смысле, если граница абсолютной погрешности числа а не превосходит единицы того разряда, в котором записывается цифра m.
Определение 3. Цифра m приближенного числа а называется верной в строгом смысле, если граница абсолютной погрешности числа а не превосходит половины единицы того разряда, в котором записана цифра m.
В числах, полученных в результате измерений или вычислений и используемых при расчетах в качестве исходных данных, а также в десятичной записи приближенного значения, все цифры должны быть верными.
Цифры в записи приближенного числа, о которых не известно, являются ли они верными, называются сомнительными.
Значащими цифрами приближенного числа называются все его верные цифры, кроме нулей, стоящих перед первой цифрой.
Пример 2. Указать верные цифры ( в строгом смысле) следующего числа 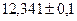 .
.
Решение. Начнем проверку
«1» относится к разряду десятки, 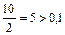 , следовательно 1 – цифра верная;
, следовательно 1 – цифра верная;
«2» относится к разряду единиц, 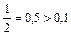 , следовательно 2 – цифра верная;
, следовательно 2 – цифра верная;
«3» относится к разряду десятых, 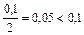 , следовательно 3 – цифра неверная.
, следовательно 3 – цифра неверная.
Таким образом число 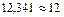 с точностью до 0,1.
с точностью до 0,1.
Пример 3. Число 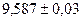 округлить до первоговерного разряда.
округлить до первоговерного разряда.
Решение. Так как цифры «9» и «5» верные, то 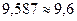 .
.
Определение 4: Относительной погрешностью 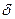 приближеного значения а числа х называется отношение абсолютной погрешности
приближеного значения а числа х называется отношение абсолютной погрешности 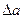 этого приближения к числу а, т.е.
этого приближения к числу а, т.е. 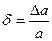 .
.
Пример 4. Найти относительную погрешность числа 6,8, если обе цифры его верные.
Решение. По условию 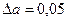 , поэтому
, поэтому 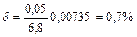 .
.
Действия над приближенными числами
| Функция | Граница абсолютной погрешности | Граница относительной погрешности |
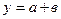 | 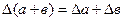 | 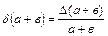 |
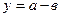 | 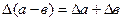 | 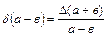 |
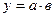 | 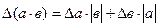 | 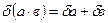 |
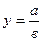 | 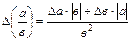 | 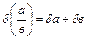 |
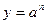 | 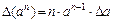 | 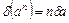 |
Примеры решения задач
Пример 5. Найдите относительную погрешность вычисления площади прямоугольника со сторонами 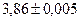 и
и 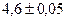 .
.
Решение. 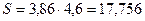 ,
, 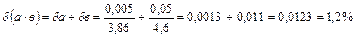
Пример 6. С какой точностью надо измерить радиус круга, чтобы абсолютная погрешность площади круга не превышала 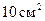 ? Грубое приближенное значение R = 8,7 см.
? Грубое приближенное значение R = 8,7 см.
Решение. Площадь круга равна 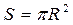 . Абсолютная погрешность площади равна
. Абсолютная погрешность площади равна 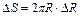 ,
, 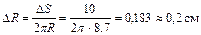 . Следовательно, если измерить величину R с погрешностью, не превышающей 0,2 см, то погрешность площади не превысит
. Следовательно, если измерить величину R с погрешностью, не превышающей 0,2 см, то погрешность площади не превысит 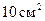 .
.
Порядок выполнения работы
1. Найдите относительную погрешность равенства 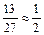 .
.
2. Число 8,75 найдено с относительной погрешностью 0,4%. Определите границу абсолютной погрешности.
3. Найдите относительную погрешность вычисления площади прямоугольника со сторонами 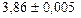 и
и 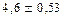 .
.
4. Найдите относительную погрешность вычисления объема прямоугольного параллелепипеда с измерениями 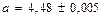 ,
, 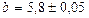 и
и 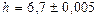 .
.
