Линейная зависимость и независимость геометрических векторов
Заметим, что в дальнейшем, не нарушая общности, будем рассматривать случай векторов в трехмерном пространстве. На плоскости рассмотрение векторов производится аналогично. Как уже отмечалось выше, все результаты, известные из курса линейной алгебры для алгебраических векторов можно перенести на частный случай геометрических векторов. Так и поступим.
Пусть зафиксированы векторы 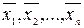 .
.
Определение.Сумма 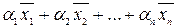 , где
, где 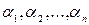 - некоторые числа, называется линейной комбинацией векторов
- некоторые числа, называется линейной комбинацией векторов 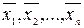 . При этом указанные числа будем называть коэффициентами линейной комбинации.
. При этом указанные числа будем называть коэффициентами линейной комбинации.
Нас будет интересовать вопрос о возможности равенства линейной комбинации нулевому вектору. В соответствии со свойствами и аксиомами векторных пространств, становится очевидным, что для любой системы векторов 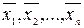 существует тривиальный (нулевой) набор коэффициентов
существует тривиальный (нулевой) набор коэффициентов 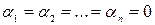 , для которого это равенство выполняется:
, для которого это равенство выполняется:
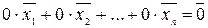 .
.
Возникает вопрос о существовании для данной системы векторов нетривиального набора коэффициентов (среди которых есть хотя бы один ненулевой коэффициент), для которого выполняется упомянутое равенство. В соответствии с этим будем различать линейно зависимые и независимые системы.
Определение.Система векторов 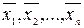 называется линейно независимой, если существует такой набор чисел
называется линейно независимой, если существует такой набор чисел 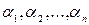 , среди которых есть хотя бы одно ненулевое, такое что соответствующая линейная комбинация равна нулевому вектору:
, среди которых есть хотя бы одно ненулевое, такое что соответствующая линейная комбинация равна нулевому вектору:
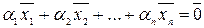 .
.
Система векторов 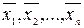 называется линейно независимой, если равенство
называется линейно независимой, если равенство
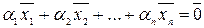
возможно лишь в случае тривиального набора коэффициентов:
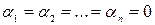 .
.
Перечислим доказываемые в курсе линейной алгебры основные свойства линейно зависимых и независимых систем.
1. Любая система векторов, содержащая нулевой вектор, является линейно зависимой.
2. Пусть в системе векторов 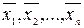 есть линейно зависимая подсистема. Тогда и вся система также является линейно зависимой.
есть линейно зависимая подсистема. Тогда и вся система также является линейно зависимой.
3. Если система векторов является линейно независимой, то любая ее подсистема также является линейно независимой.
4. Если в системе векторов есть два вектора, один из которых получается из другого умножением на некоторое число, то вся система является линейно зависимой.
Теорема (критерий линейной зависимости).Система векторов является линейно зависимой тогда и только тогда, когда один из векторов этой системы представим в виде линейной комбинации остальных векторов системы.
С учетом критерия коллинеарности двух векторов можно утверждать, что критерием их линейной зависимости является их коллинеарность. Для трех векторов в пространстве справедливо следующее утверждение.
Теорема (критерий линейной зависимости трех геометрических векторов).Три вектора 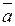 ,
, 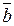 и
и 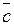 линейно зависимы тогда и только тогда, когда они компланарны.
линейно зависимы тогда и только тогда, когда они компланарны.
Доказательство.
Необходимость.Пусть векторы 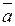 ,
, 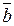 и
и 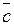 линейно зависимы. Докажем их компланарность. Тогда по общему критерию линейной зависимости алгебраических векторов утверждаем, что один из указанных векторов представим в виде линейной комбинации остальных векторов. Пусть, например,
линейно зависимы. Докажем их компланарность. Тогда по общему критерию линейной зависимости алгебраических векторов утверждаем, что один из указанных векторов представим в виде линейной комбинации остальных векторов. Пусть, например,
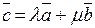 .
.
Если все три вектора 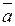 ,
, 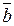 и
и 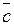 приложить к общему началу
приложить к общему началу 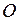 , то вектор
, то вектор 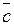 совпадет с диагональю параллелограмма, построенного на векторах
совпадет с диагональю параллелограмма, построенного на векторах 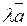 и
и 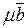 . Но это означает, что векторы
. Но это означает, что векторы 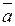 ,
, 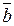 и
и 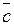 лежат в одной плоскости, т.е. компланарны.
лежат в одной плоскости, т.е. компланарны.
Достаточность.Пусть векторы 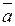 ,
, 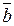 и
и 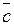 компланарны. Покажем, что они линейно зависимы. В первую очередь рассмотрим случай, когда какая-нибудь пара из указанных векторов коллинеарна. В этом случае согласно предыдущей теореме система векторов
компланарны. Покажем, что они линейно зависимы. В первую очередь рассмотрим случай, когда какая-нибудь пара из указанных векторов коллинеарна. В этом случае согласно предыдущей теореме система векторов 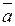 ,
, 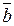 ,
, 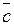 содержит линейно зависимую подсистему и, следовательно, сама является линейно зависимой согласно свойству 2 линейно зависимых и независимых систем векторов. Пусть теперь ни одна пара рассматриваемых векторов не коллинеарна. Перенесем все три вектора на одну плоскость и приведем их к общему началу
содержит линейно зависимую подсистему и, следовательно, сама является линейно зависимой согласно свойству 2 линейно зависимых и независимых систем векторов. Пусть теперь ни одна пара рассматриваемых векторов не коллинеарна. Перенесем все три вектора на одну плоскость и приведем их к общему началу 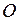 . Проведем через конец
. Проведем через конец 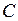 вектора
вектора 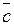 прямые параллельные векторам
прямые параллельные векторам 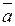 и
и 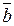 . Обозначим буквой
. Обозначим буквой 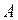 точку пересечения прямой, параллельной вектору
точку пересечения прямой, параллельной вектору 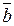 , с прямой, на которой лежит вектор
, с прямой, на которой лежит вектор 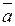 , а буквой
, а буквой 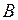 точку пересечения прямой, параллельной вектору
точку пересечения прямой, параллельной вектору 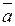 , с прямой, на которой лежит вектор
, с прямой, на которой лежит вектор 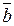 . По определению суммы векторов получаем:
. По определению суммы векторов получаем:
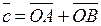 .
.
Так как вектор 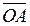 коллинеарен ненулевому вектору
коллинеарен ненулевому вектору 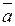 , то существует действительное число
, то существует действительное число 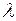 такое, что
такое, что
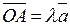 .
.
Из аналогичных соображений вытекает существование действительного числа 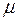 такого, что
такого, что
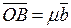 .
.
В результате будем иметь:
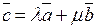 .
.
Тогда из общего критерия линейной зависимости алгебраических векторов получаем, что векторы 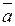 ,
, 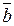 ,
, 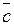 линейно зависимы. ■
линейно зависимы. ■
Теорема (линейная зависимость четырех векторов).Любые четыре вектора линейно зависимы.
Доказательство. В первую очередь, рассмотрим случай, когда какая-нибудь тройка из указанных четырех векторов компланарна. В этом случае эта тройка линейно зависима в соответствии с предыдущей теоремой. Следовательно, в соответствии со свойством 2 линейно зависимых и независимых систем векторов, и вся четверка линейно зависима.
Пусть теперь среди рассматриваемых векторов никакая тройка векторов не компланарна. Приведем все четыре вектора 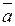 ,
, 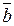 ,
, 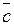 ,
, 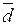 к общему началу
к общему началу 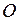 и проведем через конец
и проведем через конец 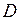 вектора
вектора 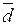 плоскости, параллельные плоскостям, определяемыми парами векторов
плоскости, параллельные плоскостям, определяемыми парами векторов 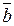 ,
, 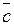 ;
; 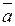 ,
, 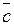 ;
; 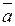 ,
, 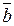 . Точки пересечения указанных плоскостей с прямыми, на которых лежат векторы
. Точки пересечения указанных плоскостей с прямыми, на которых лежат векторы 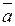 ,
, 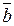 и
и 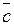 , обозначим соответственно буквами
, обозначим соответственно буквами 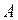 ,
, 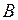 и
и 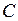 . Из определения суммы векторов следует, что
. Из определения суммы векторов следует, что
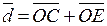 ,
,
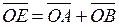 ,
,
И, соответственно,
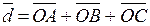 .
.
Так как вектор 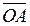 коллинеарен ненулевому вектору
коллинеарен ненулевому вектору 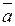 , то в соответствии с критерием линейной зависимости двух векторов получаем:
, то в соответствии с критерием линейной зависимости двух векторов получаем:
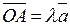 .
.
Из аналогичных соображений следует существование действительных чисел 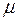 и
и 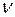 таких, что
таких, что
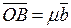 ,
,
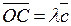 .
.
В результате получаем равенство:
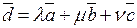 ,
,
которое с учетом общего критерия линейной зависимости алгебраических векторов говорит о том, что все четыре вектора линейно зависимы. ■
