Разложение знаменателя дроби на множители
ИКТИБ ИТА ЮФУ
КУРС ЛЕКЦИЙ ПО МАТЕМАТИКЕ
Лекция 23 Интегрирование рациональных функций
Важнейший случай, когда неопределенный интеграл может быть вычислен в явном виде, - это интеграл от так называемой рациональной функции.
Определение 1. Рациональной называется функция, равная отношению двух многочленов, т. е. это функция вида 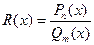 . (1).
. (1).
Здесь 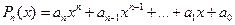 - многочлен степени
- многочлен степени 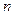 ,
, 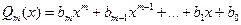 - многочлен степени
- многочлен степени 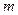 . При
. При 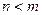 рациональная функция (1) называется правильной дробью, при
рациональная функция (1) называется правильной дробью, при 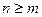 рациональная функция (1) называется неправильной дробью.
рациональная функция (1) называется неправильной дробью.
План вычисления интеграла от рациональной функции
При вычислении интеграла 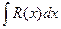 от рациональной функции разумно действовать по следующему плану.
от рациональной функции разумно действовать по следующему плану.
Шаг № 1. Преобразование неправильной дроби в правильную. Если степень числителя больше или равна степени знаменателя, то мы числитель делим на знаменатель и приходим к интегрированию правильной дроби и многочлена.
Пример 1. Представьте неправильную дробь 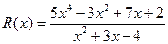 в виде суммы многочлена степени 2 (4-2=2) и правильной дроби.
в виде суммы многочлена степени 2 (4-2=2) и правильной дроби.
Решение. После деления «в столбик» найдем частное от деления 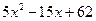 и остаток
и остаток 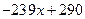 . Тем самым получим равенство
. Тем самым получим равенство 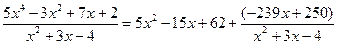 .
.
Шаг № 2. Разложение знаменателя дроби на множители. Знаменатель подынтегральной функции является многочленом и, следовательно, представляется в виде произведения линейных и квадратичных множителей.
Пример 2. Знаменатель 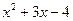 в заданной дроби разлагается на линейные множители, т. е. справедливо равенство
в заданной дроби разлагается на линейные множители, т. е. справедливо равенство 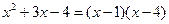 .
.
Шаг № 3. Представление правильной дроби в виде суммы простейших дробей. Правильная дробь, т. е. рациональная функция, степень числителя которой меньше степени знаменателя, представляется в виде так называемых простейших дробей. Это дроби вида: 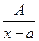 ,
, 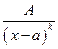 ,
, 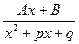 ,
, 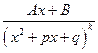 .
.
Пример 3. Представьте правильную дробь 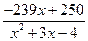 в виде
в виде 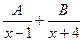 .
.
Решение. Рассмотрим равенство 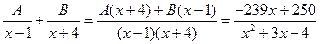 , которое имеет решение
, которое имеет решение 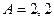 ,
, 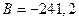 .
.
Шаг № 4. Интегрирование простейших дробей.
Мы узнаем, как вычислить интегралы вида: 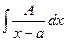 ,
, 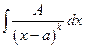 ,
, 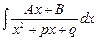 ,
, 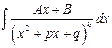 .
.
Преобразование неправильной дроби в правильную
Еще из школы мы знаем, что дробь равна частному плюс остаток, деленный на знаменатель, т. е. справедлива формула 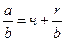 . Такая же формула справедлива для многочленов
. Такая же формула справедлива для многочленов 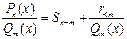 . Здесь
. Здесь 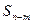 - многочлен степени
- многочлен степени 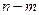 , остаток
, остаток 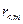 - многочлен, степень которого меньше степени знаменателя.
- многочлен, степень которого меньше степени знаменателя.
Разложение знаменателя дроби на множители
По основной теореме алгебры многочлен, степень которого больше 0, имеет хотя бы один, вообще говоря, комплексный корень. С другой стороны, по теореме Безу, если многочлен имеет корень 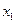 , то он делится на
, то он делится на 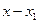 , т. е. имеет такой множитель.. Если
, т. е. имеет такой множитель.. Если 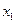 - действительное число, то мы имеем линейный множитель
- действительное число, то мы имеем линейный множитель 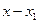 . В случае комплексного корня
. В случае комплексного корня 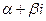 корнем многочлена с действительными коэффициентами будет также сопряженное комплексное число
корнем многочлена с действительными коэффициентами будет также сопряженное комплексное число 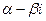 . В соответствии с теоремой Безу многочлен имеет 2 множителя
. В соответствии с теоремой Безу многочлен имеет 2 множителя 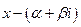 и
и 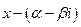 , произведение которых равно
, произведение которых равно 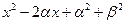 . Этот множитель является квадратичным с отрицательным дискриминантом при
. Этот множитель является квадратичным с отрицательным дискриминантом при 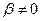 . Итак, любой многочлен, представляется в виде произведения линейных и квадратичных множителей.
. Итак, любой многочлен, представляется в виде произведения линейных и квадратичных множителей.
