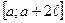Д.М.3.3. Числовые и степенные ряды. Тригонометрические ряды Фурье.

Программа экзамена по высшей математике (ФИМ, 3-ий семестр)

Уч.г.

Дисциплинарный модуль	Лекции, ч.	Пр. зан. ч.
Д.М.3.1. Интегрирование функции нескольких переменных (кратные и криволинейные интегралы).
Д.М.3.2. Поверхностные интегралы. Векторный анализ и элементы теории поля.
Д.М.3.3. Числовые и степенные ряды. Гармонический анализ. Тригонометрические ряды Фурье.
ИТОГО за 3 семестр	36ч	36ч

Д.М.3.1. Кратные и криволинейные интегралы.

1.Определение и свойства двойного интеграла.

2. Вычисление двойного интеграла в декартовых координатах.

3.Вычисление двойного интеграла в полярных координатах.

4.Приложения двойного интеграла (площадь области, объем тела, площадь поверхности).

5. Тройной интеграл, вычисление в декартовой системе координат.

6. Тройной интеграл в цилиндрических и сферических координатах.

7. Приложения тройного интеграла (объем тела, масса).

8. Криволинейный интеграл 1-го рода. Определение и вычисление.

9. Криволинейный интеграл 2-го рода. Определение и вычисление.

10. Криволинейный интеграл 2-го рода. Частные случаи. Формула Грина.

Д.М. 3.2. Поверхностные интегралы. Элементы теории поля.

11. Поверхностные интегралы I-го рода. Вычисление. Приложение.

12. Поверхностные интегралы II-го рода. Способы вычисления. Теорема Гаусса –Остроградского.

13. Скалярное поле. Поверхности уровня. Производная по направлению. Градиент, его свойства.

14. Векторное поле. Дивергенция. Ротор, его свойства.

15.Поток векторного поля. Формула Остроградского – Гаусса.

16. Циркуляция векторного поля. Формула Стокса.

17. Потенциальные, соленоидальные и гармонические векторные поля.

18. Вычисление потенциала потенциального векторного поля.

Д.М.3.3. Числовые и степенные ряды. Тригонометрические ряды Фурье.

19.Определение числового ряда и его суммы. Сходимость знакоположительных числовых рядов.

20. Свойства сходящихся числовых рядов. Необходимый признак сходимости ряда.

21. Гармонический ряд, ряд геометрической прогрессии, их сходимость. Таблица известных рядов.

22. Достаточные признаки сходимости знакоположительных рядов:

1) I-ый и II-ой (предельный) признаки сравнения.

2) признак Даламбера.

3) признаки Коши – радикальный и интегральный.

23. Знакочередующиеся числовые ряды. Теорема Лейбница.

24. Абсолютно и условно сходящиеся ряды. Свойства абсолютно сходящихся рядов.

25.Функциональные ряды. Степенные ряды. Теорема Абеля. Область сходимости степенного ряда.

26. Разложение функций в степенной ряд. Ряды Тейлора и Маклорена.

27.Таблица разложений в ряд Маклорена некоторых элементарных функций.

28. Приближенные вычисления с помощью степенных рядов (вычисление значения функции, вычисление определенных интегралов, решение дифференциальных уравнений).

29. Гармонический анализ. Тригонометрический ряд Фурье. Теорема Дирихле.

30. Разложение в ряд Фурье функций периода 2 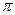. Коэффициенты Фурье.

31. Разложение в ряд Фурье чётных и нечетных функций периода 2 .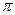

32. Разложение в ряд Фурье функций произвольного периода .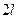

33. Разложение в ряд Фурье четных и нечётных функций периода .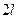

34. Разложение в ряд Фурье функций периода 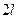, заданных на полупериоде.

35. Разложение в ряд Фурье функций, заданных на произвольном отрезке