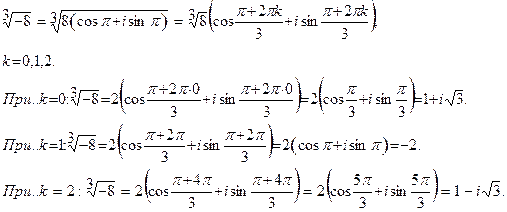Ряды Фурье(тригонометрические.)

Определение:

Функция f(x) называется кусочно-непрерывной на <a;b>, если этот промежуток можно разбить на конечное число промежутков 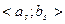на каждом из которых:

1) функция f(x) ограниченна и непрерывна во внутренних точках;

2) на концах существуют конечные односторонние пределы.

Под интегралом от такой функции понимается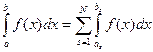

Определение

Назовем функцию f(x) кусочно-гладкой на <a;b>, если f(x) и 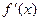кусочно-непрерывной на<a;b>.

Определение

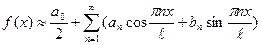- тригонометрический ряд Фурье , где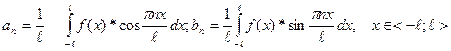

Определение

Скалярным произведением функций 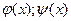называется интеграл: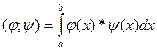

Определение

Нормой функции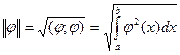

Определение

Функции 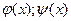называются ортогональными на <a;b> если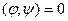

Определение

Основной системой тригонометрических функций называется система 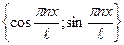(1) общий период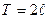

Т. Основные тригонометрические функции(1) попарно ортогональны на любом промежутке длины 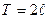, то есть:

1)

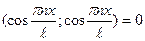
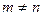
2)

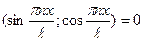
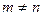
3)

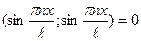
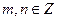
Вывод:(непосредственно).

Замечание: Нормы основных тригонометрических функций

;

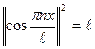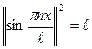
Определение

Представление функции f(x) в виде суммы бесконечного или конечного числа гармоник: 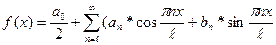(2) – называется тригонометрическим рядом Фурье.

Вывод коэффициентов ряда Фурье.

1) проинтегрируем (2)

2) умножим (2) на 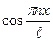и интегрируем.

3) Умножим (2) на 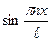и интегрируем.

A_n и b_n - коэффициенты Фурье для f(x)

Ряд называется рядом Фурье независимо от того, будет ли f(x) являтся суммой этого ряда или нет.

Теорема(теорема сходимости ряда Фурье)

Пусть периодическая функция f(x) определена на 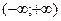кроме может быть точек её разрыва и имеющая период 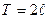>0, является кусочно гладкой на любом промежутке длиной .

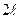Тогда: 1) тогда её ряд сходится 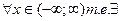- сумма ряда Фурье.

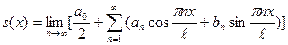
2) сумма ряда Фурье s(x) равна функции f(x) в точках непрерывности её и равна среднему арифметическому пределов слева и справа в точках x₀ разрыва функции

Т.е.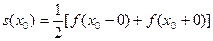

Замечание: 1⁰. Если f(x) – четная периодическая функция то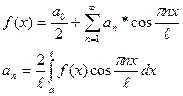

2⁰. Если f(x) нечетная периодическая функция то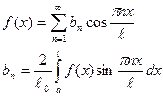

3⁰. Если кусочно гладкая функция f(x) не является периодической , то можно построить представление этой функции в виде ряда Фурье на любом конечном промежутке. Для этого построим периодическую функцию 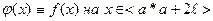с периодом 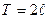путем параллельных сдвигов вдоль 0X.

Комплексные числа

Выражение вида z=x+yi=ρ(cosφ + i sinφ) называется комплексным числом (в алгебраической и тригонометрической форме соответственно). Здесь i² = -1, x = Re(z) — действительная часть, a y=Im(z) — мнимая часть комплексного числа z, р и φ — соответственно, модуль и аргумент числа z:

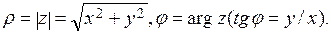(7)

Комплексные числа изображаются точками (рис.4) на комплексной плоскости.

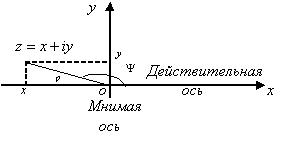
Рисунок 4 – изображение комплексного числа

Извлечение корня п – й степени (п – натуральное число) из числа z = ρ(cosφ + i sinφ) (z 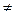0) производится по формуле

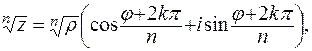(8)

где 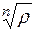— арифметический корень из модуля z, a k = 0,1, …, n – 1.

Пример . Изобразить на комплексной плоскости числа 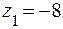, 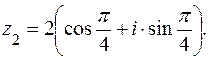Записать число z₁ в тригонометрической, а число z₂ — в алгебраической форме.

Решение. 1) Для числах z₁ имеем x₁ = Re z₁ = -8 , y₁ = Im z₁ = 0. Откладывая по оси Ox х₁ = -8, а по оси Оу у₁ = 0, получаем точку комплексной плоскости, соответствующую числу z₁ (рис. 8). Модуль этого числа находим по формуле (7): 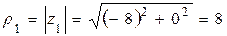. Аргумент определяемиз равенства 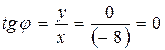. Taккак число z₁ находится в левой полуплоскости, то его аргумент 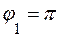. Тригонометрическая форма числа z₁ имеет вид .

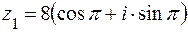2) Модуль числа z₂ равен 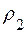, а аргумент 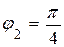. Для его изображения на комплексной плоскости проводимиз полюса луч под углом 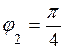к полярной оси и откладываем на нем отрезок длиной р₂ = 2. Полученная точка соответствует числу z₂ (рис. 8). Егодействительнаячасть 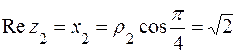, а мнимая часть 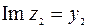, 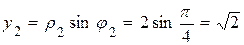. Таким образом, алгебраическая формачисла z₂ имеетвид .

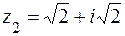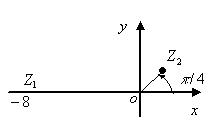
Рисунок 8 – графическое изображение числа z₂

Пример.Вычислить .

Решение. Модуль числа -8 равен 8, а аргумент равен 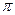. Используя формулу (8), получаем