Производная по направлению. Градиент

Скалярным полем называется часть пространства (или все пространство), каждой точке которой соответствует численное значение некоторой скалярной величины.

Примеры

Тело, имеющее в каждой точке определенное значение температуры – скалярное поле.

Неоднородное тело, каждой точке которой соответствует определенная плотность – скалярное поле плотности.

Во всех этих случаях скалярная величина U не зависит от времени, а зависит от положения (координат) точки М в пространстве, то есть 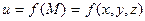-- это функция трех переменных, она называется функцией поля. И обратно, всякая функция трех переменных u=f(x, y, z) задает некоторое скалярное поле.

Функция плоского скалярного поля зависит от двух переменных z=f(x, y).

Рассмотрим скалярное поле u=f(x, y, z).

Вектор, координатами которого являются частные производные функции, вычисленные в заданной точке, называется градиентом функции в этой точке.

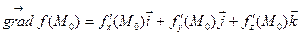
или

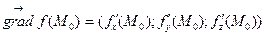
Рассмотрим некоторый вектор 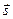и на нем две точки M₀(x₀, y₀, z₀) и 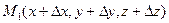. Найдем приращение функции в направлении :

.

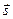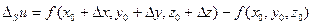Производной по направлению называется следующий предел, если он существует:

.

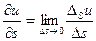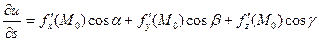
где 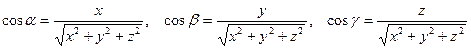-- направляющие косинусы вектора 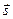; α, β, γ -- углы, которые образует вектор с осями координат.

Для функции двух переменных эти формулы принимают вид:

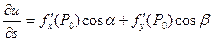или ,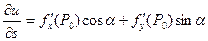

так как .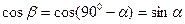

Между градиентом и производной по направлению в одной и той же точке существует связь.

Теорема. Скалярное произведение градиента функции на вектор некоторого направления равно производной данной функции в направлении этого вектора:

.

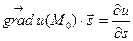Следствие.Производная по направлению имеет наибольшее значение, если это направление совпадает с направлением градиента (обосновать самостоятельно, используя определение скалярного произведения и считая, что ).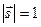

Выводы:

1. Градиент – это вектор, показывающий направление наибольшего возрастания функции в данной точке и имеющий модуль, численно равный скорости этого возрастания:

.

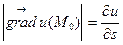2. Производная по направлению – это скорость изменения функции в направлении 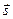: если 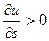, то функция в этом направлении возрастает,

если 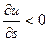, то функция убывает.

3. Если вектор 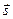совпадает с одним из векторов 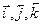, то производная по направлению этого вектора совпадает с соответствующей частной производной.

Например, если 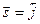, тогда .

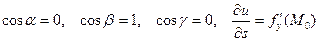Пример (см. задание VII)

Даны функция 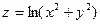, точка А(1, 2) и вектор .

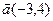Найти: 1) ;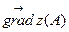

2) .

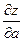Решение.

1) найдем частные производные функции и вычислим их в точке А.

, .

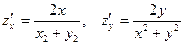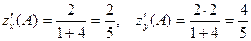Тогда .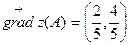

2) Найдем направляющие косинусы вектора :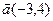

.

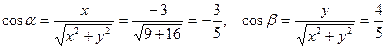Тогда .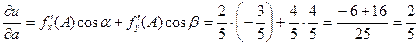

Ответ: ;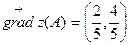

.

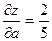Ниже приведены задания для контрольной работы.

Номер варианта соответствует последней цифре Вашего шифра зачетной книжки. Из каждого задания необходимо выполнить пример, номер которого совпадает с номером Вашего варианта.

Каждую контрольную работу следует выполнять в отдельной тетради. Следует указать свой шифр и номер варианта. Условие задачи должно быть полностью переписано перед ее решением.

Отмеченные рецензентом ошибки необходимо исправить в конце работы, сделав работу над ошибками.

Зачтенные контрольные работы предъявляются студентом при сдаче зачета или экзамена.

ЗАДАНИЕ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ

IПо координатам вершины пирамиды А₁А₂А₃А₄ найти:

1) длину ребра А₁А₂;

2) угол между ребрами А₁А₂ и А₁А₄;

3) угол между ребром А₁А₄ и гранью А₁А₂А₃;

4) площадь грани А₁А₂А₃;

5) объем пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости А₁А₂А₃;

8) уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃.

1. А₁(4, 2, 5), А₂(0, 7, 2), А₃(0, 2, 7), А₄(1, 5, 0)

2. А₁(4, 4, 10), А₂(4,10, 2), А₃(2, 8, 4), А₄(9, 6, 4)

3. А₁(4, 6, 5), А₂(9, 6, 4), А₃(2,10,10), А₄(7, 5, 9)

4. А₁(3, 5, 4), А₂(8, 7, 4), А₃(5,10, 4), А₄(4, 7, 8)

5. А₁(10, 6, 6), А₂(-2, 8, 2), А₃(6, 8, 9), А₄(7,10, 3)

6. А₁(1, 8, 2), А₂(5, 2, 6), А₃(5, 7, 4), А₄(4,10, 9)

7. А₁6, 6, 5), А₂(4, 9, 5), А₃(4, 6,11), А₄(6, 9, 3)

8. А₁(7, 2, 2), А₂(5, 7, 7), А₃(5, 3, 1), А₄(2, 3, 7)

9. А₁(8, 6, 4), А₂(10, 5, 5), А₃(5, 6, 8), А₄(8,10, 7)

10. А₁(7, 7, 3), А₂(6, 5, 8), А₃(3, 5, 8), А₄(8, 4, 1)

II1. Даны вершины треугольника АВС: А(-3, 1), В(0, 4), С(2, 5). Написать уравнение высоты, проведенной из вершины С к стороне АВ.

2. Стороны треугольника АВС заданы уравнениями:

x+y=2 (AB), 2x-y=-2 (AC), x-2y=2 (BC).

Написать уравнение высоты, проведенной из вершины А к стороне ВС.

3. Даны вершины треугольника АВС: А(4, -2), В(3, -1), С(2, 6). Написать уравнение средней линии ΔАВС, параллельной стороне АС.

4. Стороны треугольника АВС заданы уравнениями:

x+y-3=0 (AB), y-2x=0 (AC), x-y-1=0 (BC).

Написать уравнение прямой, проходящей через вершину А параллельно стороне ВС.

5. Даны вершины четырехугольника A(0, 6), B(7,12), C(6, 2), D(2, 2). Найти точку пересечения его диагоналей.

6. Даны вершины треугольника АВС: А(0, 4), В(-3, 2), С(2, 6). Написать уравнение медианы, проведенной из точки В.

7. Даны вершины треугольника АВС: А(2, 4), В(-2, 5), С(-1, 2). Написать уравнение высоты, проведенной из вершины А к стороне ВС.

8. Даны вершины трапеции A(-2,-3), B(-3, 1), C(7, 7), D(3, 0). Написать уравнение средней линии трапеции.

9. В треугольнике MNP написать уравнение медианы, проведенной из вершины М, если известно, что М(4, -1), N(2, 3), P(-4, -2).

10. Стороны треугольника лежат на прямых:

x-y=-2 (AB), x+y=1 (BC), x-2y=1 (AC). Написать уравнение высоты, опущенной из вершины В на сторону АС.

IIIРешить систему линейных уравнений, используя формулы Крамера.

1.	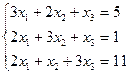2.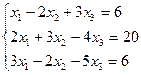
3.	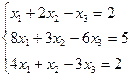4.
5.	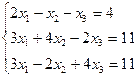6.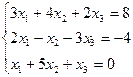
7.	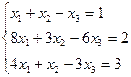8.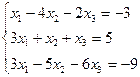
9.	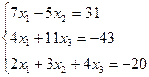10.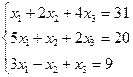

IV Вычислить пределы функций, не пользуясь правилом Лопиталя.

1.	a)	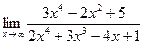b)	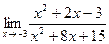c)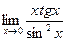
2.	a)	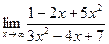b)	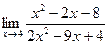c)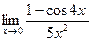
3.	a)	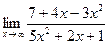b)	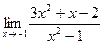c)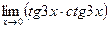
4.	a)	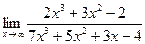b)	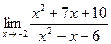c)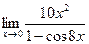
5.	a)	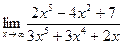b)	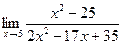c)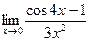
6.	a)	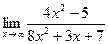b)	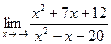c)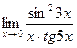
7.	a)	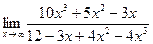b)	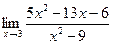c)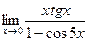
8.	a)	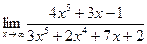b)	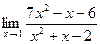c)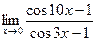
9.	a)	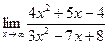b)	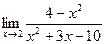c)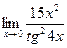
10.	a)	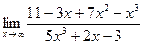b)	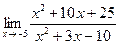c)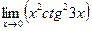

V Найти производные первого порядка, используя правила вычисления производных.

1.	a)	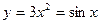b)	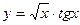c)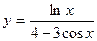
2.	a)	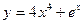b)	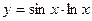c)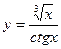
3.	a)	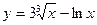b)	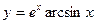c)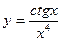
4.	a)	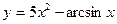b)	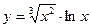c)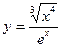
5.	a)	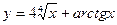b)	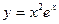c)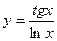
6.	a)	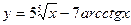b)	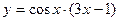c)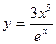
7.	a)	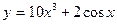b)	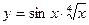c)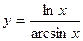
8.	a)	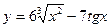b)	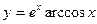c)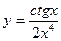
9.	a)	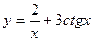b)	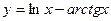c)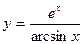
10.	a)	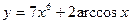b)	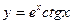c)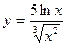

VIИсследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить график.

1.	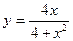2.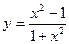
3.	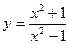4.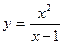
5.	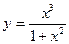6.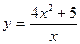
7.	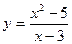8.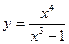
9.	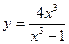10.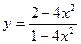

VIIДана функция 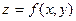, точка 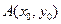и вектор 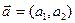. Найти:

1) grad z в точке А;

2) производную в точке А по направлению вектора .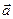

1.	Z=x2+xy+y2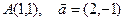
2.	Z=2x2+3xy+y2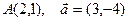
3.	Z=ln(5x2+3y2)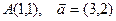
4.	Z=ln(5x2+4y)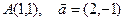
5.	Z=5x2+6xy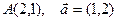
6.	Z=arctg(xy2)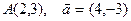
7.	Z=arcsin(x2/y)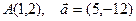
8.	Z=ln(3x2+4y2)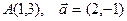
9.	Z=3x4+2x2y3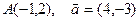
10.	Z=3x2y3+5xy2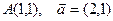

МАТЕМАТИКА

I ЧАСТЬ

Составители: Арутюнян Ашот Страевич

Горшкова Светлана Николаевна

Данович Лариса Михайловна

Наумова Наталья Александровна

Петрушина Ирина Игоревна

Редактор Л.В. Троицкая

Компьютерная верстка Н.А.Наумовой

Подписано в печать Формат

Бумага оберточная Офсетная печать

Печ.л. 2,25 Изд.№ 136

Усл.печ.л. 2,0 Тираж

Уч.-изд.л. 1,5 Заказ №