Линейные дифференциальные уравнения первого порядка
Определение 8. Дифференциальное уравнение вида:
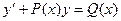 ,
, 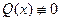 . (4)
. (4)
называется линейным уравнением.
Решение линейного уравнения можно искать в виде: 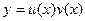 ,
, 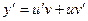 . Значения для
. Значения для 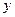 и
и 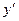 подставим в данное уравнение. В результате получим тождество:
подставим в данное уравнение. В результате получим тождество: 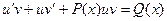 (5)
(5)
Так так неизвестных функций две, а условие, которому они удовлетворяют одно, то для нахождения 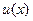 и
и 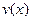 надо иметь еще одно условие, которое мы наложим по своему усмотрению. В левой части равенства (5) сумму первого и третьего слагаемых приравняем к 0, т.е.
надо иметь еще одно условие, которое мы наложим по своему усмотрению. В левой части равенства (5) сумму первого и третьего слагаемых приравняем к 0, т.е. 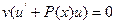 . Функция
. Функция 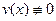 , т.к. в этом случае
, т.к. в этом случае 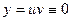 , а тождественный ноль не является решением уравнения (4) следовательно,
, а тождественный ноль не является решением уравнения (4) следовательно, 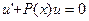 . Последнее уравнение является дифуравнением с разделяющимися переменными, решая это уравнение, найдем функцию
. Последнее уравнение является дифуравнением с разделяющимися переменными, решая это уравнение, найдем функцию 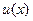 :
: 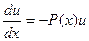 ;
; 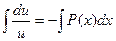 ;
; 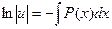 ;
; 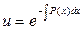 . При нахождении функции
. При нахождении функции 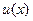 произвольную постоянную С можно не добавлять, т.к. нам достаточно найти какую-либо функцию
произвольную постоянную С можно не добавлять, т.к. нам достаточно найти какую-либо функцию 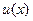 , а произвольную постоянную запишем при нахождении
, а произвольную постоянную запишем при нахождении 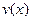 . Найденную функцию
. Найденную функцию 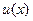 подставим в равенство (5), в результате получим еще одно дифуравнение с разделяющими переменными:
подставим в равенство (5), в результате получим еще одно дифуравнение с разделяющими переменными: 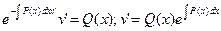 ;
;
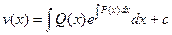 ;
; 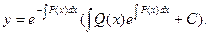 Таким образом, решение линейного дифуравнения первого порядка заменой
Таким образом, решение линейного дифуравнения первого порядка заменой 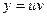 сводится к решению двух дифуравнений с разделяющимися переменными.
сводится к решению двух дифуравнений с разделяющимися переменными.
Пример 7. Проинтегрировать уравнение 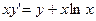 , найти интегральную кривую этого уравнения, проходящую через точку
, найти интегральную кривую этого уравнения, проходящую через точку 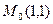 .
.
Решение. Обе части уравнения поделим на x, в результате получим линейное уравнение первого порядка 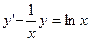 . Решение этого уравнения будем искать в виде
. Решение этого уравнения будем искать в виде 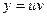 ,
, 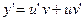 . Выражение для
. Выражение для 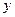 и
и 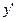 подставим в данное уравнение:
подставим в данное уравнение: 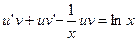 (6)
(6)
Далее сумму первого и третьего слагаемых приравняем к 0. Т.к. 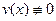 , то
, то 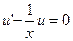 . Последнее уравнение является дифуравнением с разделяющимися переменными:
. Последнее уравнение является дифуравнением с разделяющимися переменными:
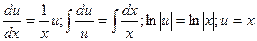 .
.
Найденное значение 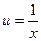 подставим в равенство (6), в результате получим:
подставим в равенство (6), в результате получим: 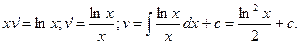 Следовательно, общее решение данного уравнения запишется в виде:
Следовательно, общее решение данного уравнения запишется в виде: 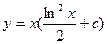 . Теперь из общего решения выделим интегральную кривую, которая проходит через точку
. Теперь из общего решения выделим интегральную кривую, которая проходит через точку 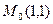 .
. 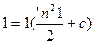 . с=1; Полученное значение с=1 подставим в общее решение и получим искомую интегральную кривую
. с=1; Полученное значение с=1 подставим в общее решение и получим искомую интегральную кривую 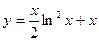 .
.
Уравнения Бернулли
Определение 9. Уравнение вида
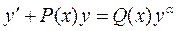 (7)
(7)
называется уравнением Бернулли. Если 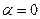 , то уравнение (7) является линейным. Если
, то уравнение (7) является линейным. Если 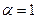 , то уравнение (7) является уравнением с разделяющимися переменными.
, то уравнение (7) является уравнением с разделяющимися переменными.
Если 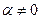 и
и 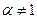 , то мы получаем новый тип уравнения, который ранее не рассматривали.
, то мы получаем новый тип уравнения, который ранее не рассматривали.
Решение уравнения Бернулли можно искать в виде 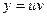 и решать это уравнение аналогично решению линейного уравнения.
и решать это уравнение аналогично решению линейного уравнения.
Пример 8. Проинтегрировать уравнение 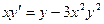 и выделить интегральную кривую, проходящую через точку
и выделить интегральную кривую, проходящую через точку 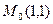 , т.е.
, т.е. 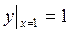 .
.
Решение. Данное уравнение запишем в виде: 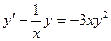 . Это уравнение является уравнением Бернулли,
. Это уравнение является уравнением Бернулли, 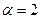 .
.
Общее решение уравнения будем искать в виде 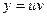 ,
, 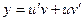 . Подставляя выражение для
. Подставляя выражение для 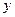 и
и 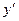 в уравнение, мы должны получить тождество
в уравнение, мы должны получить тождество
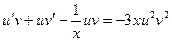 (8)
(8)
Функцию 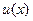 найдем из равенства
найдем из равенства 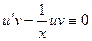 . Так как
. Так как 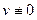 , то
, то 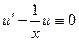 . Следовательно,
. Следовательно, 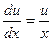 ,
, 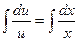 ,
, 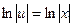 ,
, 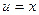 .
.
Найденное значение 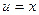 подставим в (8), в результате получим
подставим в (8), в результате получим 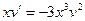 уравнение с разделяющимися переменными.
уравнение с разделяющимися переменными. 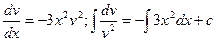 ;
; 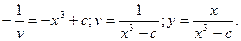 Получили общее решение данного уравнения, из которого с помощью начального условия
Получили общее решение данного уравнения, из которого с помощью начального условия 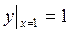 выделим требуемую интегральную кривую. В общее решение подставим
выделим требуемую интегральную кривую. В общее решение подставим 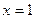 и
и 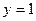 .
.
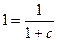 , отсюда
, отсюда 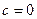 .
.
Подставляя в общее решение найденное 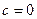 получим искомую интегральную кривую
получим искомую интегральную кривую 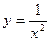 .
.
