Метод интегрирования по частям

ИКТИБ ИТА ЮФУ

КУРС ЛЕКЦИЙ ПО МАТЕМАТИКЕ

Лекция 22 Методы вычисления неопределенного интеграла

План лекции

Методы интегрирования. Интегрирование простейших и рациональных дробей. Интегрирование тригонометрических функций и некоторых иррациональных выражений.

Мы с вами узнали, что такое неопределенный интеграл - это совокупность первообразных заданной функции, т. е. множество функций, задаваемых, как мы выяснили, формулой 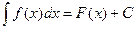. Как вычислить (взять) неопределенный интеграл? Для этого мы должны знать таблицу первообразных и правила интегрирования. Формально этих знаний достаточно для умения вычислять интегралы. Но надо понимать, что нет железобетонных (как для вычисления производных) правил (алгоритмов) для нахождения первообразных. Поэтому умение интегрировать сводится к знанию тех случаев, кода существует четкий алгоритм нахождения первообразной.

Простейшие методы интегрирования

Первый (простейший) уровень знаний и умений связан с умением вычислять такие неопределенные интегралы, в которых вычисление сводится к применению линейных свойств (первообразная от линейной комбинации функций равен линейной комбинации соответствующих первообразных) и таблицы первообразных.

Пример 1. Вычислите неопределенный интеграл .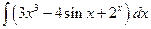

Решение. Первообразная от линейной комбинации функций 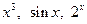равна такой же линейной комбинации соответствующих первообразных 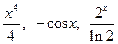. Следовательно, .

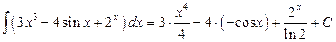Метод интегрирования по частям

Посмотрим, как можно применить формулу 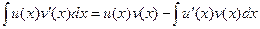интегрирования по частям в неопределенном интеграле. Наиболее естественно применить эту формулу можно в том случае, когда подынтегральную функцию в неопределенном интеграле можно представить в виде произведения двух множителей. В правой части формулы первый множитель произведения переходит в свою производную, а второй множитель – в свою первообразную. Метод интегрирования по частям в неопределенном интеграле применяют, прежде всего, в тех случаях, когда новый интеграл в правой части формулы проще первоначального интеграла в левой части. (Хотя бывают и всякие «хитрые» случаи.) Кстати, формулу интегрирования по частям в неопределенном интеграле можно записать в виде .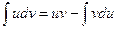

Пример 2. Вычислите неопределенный интеграл .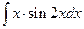

Решение. Введем обозначения 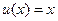, , 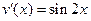тогда 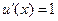, 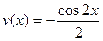и заданный интеграл преобразуется к виду 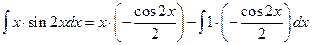, после чего мы приходим к ответу .

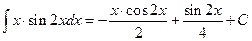Пример 3. Вычислите неопределенный интеграл .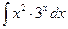

Решение. При каждом интегрировании по частям степень 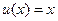будет снижаться на 1, поэтому придется дважды применять формулу интегрирования по частям. Итак, .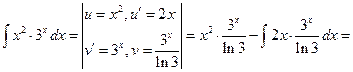

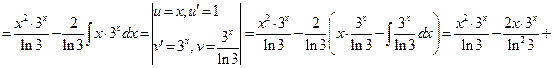
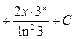Пример 4. Вычислите неопределенный интеграл .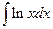

Решение. Несмотря на то, что подынтегральная функция состоит из одного множителя, мы применим метод интегрирования по частям, считая, что вторым множителем является 1. Итак,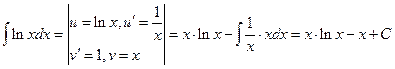

Пример 5. Вычислите неопределенный интеграл .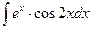

Решение. При двукратном интегрировании по частям интеграл переходит в пропорциональный заданному. Тем самым мы получим линейное уравнение для нахождения искомой первообразной. Итак, .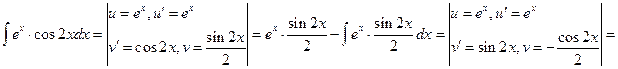

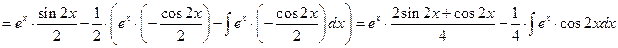Если 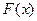- одна из первообразных функции 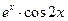, то тем самым справедливо равенство 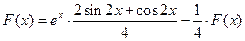, откуда 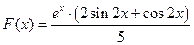и 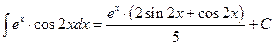.