Производная по направлению и градиент.
Модели выпуклого программирования
Постановка вопроса
Нелинейное программирование охватывает столь широкий класс задач, что универсальные эффективные численные методы решения для них в принципе не могут быть созданы. Это, в первую очередь, связано с тем, что в задачах нелинейного программирования, как правило, существуют такие допустимые (т.ею удовлетворяющие ограничениям) наборы параметров, которые являются наилучшими среди достаточно близких к ним допустимых наборов, но которые, тем не менее, не являются оптимальными, то есть, функция в этих точках не достигает глобального экстремума. Задачи такого типа называются многоэкстремальными или полимодальными.
Эффективные численные методы разработаны лишь для отдельных классов задач нелинейного программирования, про которые априори известно, что они не являются многоэкстремальными. Таковы, например, задачи выпуклого программирования.
Выпуклое программирование – это раздел нелинейного программирования, занимающийся исследованием и отысканием решений задачи минимизации выпуклой функции (максимизации вогнутой функции) на выпуклом множестве, заданном системой неравенств.
|
|
|






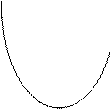



 Функция f(Х), определенная на выпуклом множестве М n-мерного пространства En, называется выпуклой на М, если для любых точек Х1 и Х2, принадлежащих М, и для любого числа λ, 0 ≤ λ≤1 справедливо неравенство
Функция f(Х), определенная на выпуклом множестве М n-мерного пространства En, называется выпуклой на М, если для любых точек Х1 и Х2, принадлежащих М, и для любого числа λ, 0 ≤ λ≤1 справедливо неравенство
|
|


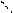 f((1- λ) Х1+ λ Х2) ≤(1- λ) f(Х1)+ λ f(Х2) (8.1)
f((1- λ) Х1+ λ Х2) ≤(1- λ) f(Х1)+ λ f(Х2) (8.1)
|
 т.е., график выпуклойфункции f(Х) расположен ниже (не выше) любой своей хорды (рис. 8.1).
т.е., график выпуклойфункции f(Х) расположен ниже (не выше) любой своей хорды (рис. 8.1).
|
|
|





 Иногда выпуклые функции называют выпуклыми вниз, а вогнутые – выпуклыми вверх.
Иногда выпуклые функции называют выпуклыми вниз, а вогнутые – выпуклыми вверх.
|
|
Если неравенство (8.1) выполняется как строгое, то функция называется строго выпуклой (или строго вогнутой).
Выпуклость (вогнутость) функции одной или двух переменных видна по ее графику.
В теории выпуклого программирования в качестве основной обычно рассматривается задача отыскания вектора 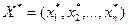 , который удовлетворяет условиям
, который удовлетворяет условиям
xj ≥ 0, j=1, 2, …, n (8.2)
gi(X) ≤ 0, i=1, 2, …, m (8.3)
и доставляет глобальный минимум функции F=f(x1, x2, …, xn). При этом заданные функции f, g1, g2, …, gm, определенные на n-мерных векторах X с неотрицательными компонентами, предполагаются выпуклыми.
Векторы, удовлетворяющие условиям (8.2) и (8.3), называются допустимыми, а искомые векторы 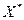 – оптимальными.
– оптимальными.
Производная по направлению и градиент.
Если функция F дифференцируема в точке Х, то она имеет в этой точке производную по любому направлению l.
Определение 1. Производной 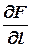 функции F(X) по направлению l в точке Х0 называется предел
функции F(X) по направлению l в точке Х0 называется предел 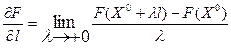 . (8.4)
. (8.4)
Направление l обычно задается вектором l = (l1, l2, …, ln).
Производная функции F по направлению l выражается через частные производные этой функции по формуле
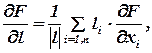 (8.5)
(8.5)
где li – длина проекции вектора l на ось хi;
|l| - длина вектора l, т.е. 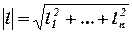 .
.
Абсолютная величина производной функции по направлению l дает скорость изменения функции в этом направлении, а знак показывает характер изменения функции (возрастание или убывание).
Определение 2. Градиентом 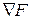 функции F(X) называется вектор, проекциями которого на координатные оси служат соответствующие частные производные этой функции, т.е.
функции F(X) называется вектор, проекциями которого на координатные оси служат соответствующие частные производные этой функции, т.е.
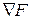 =
= 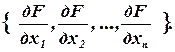
Можно показать, что max 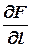 достигается тогда, когда направление l совпадает с направлением
достигается тогда, когда направление l совпадает с направлением 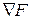 . По формуле (8.5) производная функции F по направлению
. По формуле (8.5) производная функции F по направлению 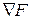 равна
равна
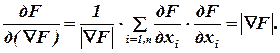
Таким образом, в каждой точке Х направление градиента является направлением наибольшего возрастания функции, а длина градиента равна наибольшей скорости возрастания функции в этой точке.
Выпуклые функции обладают следующими аналитическими и алгебраическими свойствами:
1. Если функция F(X) выпукла, то функция –F(X) вогнута.
2. Выпуклая (вогнутая) функция, определенная на выпуклом множестве М, непрерывна в каждой внутренней точке этого множества.
3. Если функции 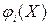 выпуклые при всех неотрицательных значениях переменных, то область решений системы неравенств
выпуклые при всех неотрицательных значениях переменных, то область решений системы неравенств 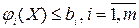 является выпуклым множеством (если она не пуста).
является выпуклым множеством (если она не пуста).
4. Всякая дифференцируемаястрого выпуклая (вогнутая) функция имеет не более одной стационарной точки (т.е. точки, в которой равны нулю все частные производные). При этом для выпуклой (вогнутой) функции стационарная точка всегда является точкой локального и глобального минимума (максимума).
5. Дважды дифференцируемая функция F(X) является выпуклой в том и только в том случае, когда
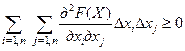 (8.6)
(8.6)
для любых Х 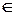 М и Δxi, Δxj, не обращающихся в нуль одновременно.
М и Δxi, Δxj, не обращающихся в нуль одновременно.
