Задания для расчётно - графических работ
Задание 1
Тема:Кинематика вращательного движения.
Формулировка задания.
Сплошной диск вращается относительно оси, проходящей через его центр масс и перпендикулярной плоскости диска. Уравнения изменения со временем кинематических характеристик вращающегося диска приведены в таблице 1. Угол поворота j задан в радианах, А = 0.0314 рад/с2, В = 0.1 рад/с.
1. Построить графики изменения со временем угла поворота j(t), модуля угловой скорости w(t) и углового ускорения b(t).
2. Для точки, находящейся на расстоянии R = 0,N м (здесь N-номер варианта), определить полное ускорение в момент времени t .
Значения параметров по вариантам.
Таблица 1
| Вариант | Заданное уравнение | Начальные условия (при t = 0) | t, с |
| 1. | b = Ае-Вt | j = 0, w = 0 | |
| 2. | j = 1-(1+Вt)-1 | - | |
| 3. | b = -A(1+Bt)-2 | j = 0, w = 0.1 p рад/с | |
| 4. | w = В(1+е-Вt) | j = 0 | |
| 5. | j = ln(1+Bt) | - | |
| 6. | j =sin Bt | - | |
| 7. | j =1 - е-Вt | - | |
| 8. | b = -A cos Bt | j = 0, w = 0.1 p рад/с | |
| 9. | w = В(1 + sin Bt) | j = 0 | |
| 10. | w = Ве-Вt | j = 0 | |
| 11. | w = В sin Bt | j = 0 | |
| 12. | b = -A sin Bt | j = 0, w = 0.1 p рад/с | |
| 13. | j = 1 - е-Вt + 2Bt | - | |
| 14. | j = B(1+Bt)-1 | j = 0 | |
| 15. | b = - A(1+Bt)-3 | j = 0, w = 0.1 p рад/с | |
| 16. | j = 2Bt – 1 + е-Вt | - | |
| 17. | w = B cos Bt | j = 0 | |
| 18. | w = В( 1- sin Bt) | j = 0 | |
| 19. | w = Bt - sin Bt | - | |
| 20. | b = A cos Bt | j = 0, w = 0 | |
| 21. | j = 1- cos Bt | - | |
| 22. | w = В(1 - е-Вt) | j = 0 | |
| 23. | b = A sin Bt | j = 0, w = 0 | |
| 24. | w = В(1+Bt)-2 | j = 0 | |
| 25. | b = A е-Вt | j = 0, w = 0.1 p рад/с |
Задание 2
Тема:Кинематиика материальной точки.
Формулировка задания.
Под действием силы материальная точка массой m движется так, что её координата меняется по закону x(t). Уравнение движения и параметры приведены в таблице 2.1 (где A, B, C и D – постоянные величины).
Определить, в момент времени Dt, следующие показатели: путь, модуль перемещения, модуль скорости, проекцию скорости и работу силы, действующей на материальную точку.
Построить графики зависимостей за интервал времени Dt приведённые в таблице 2.2
Значения параметров по вариантам.
Таблица 2.1
| Вариант | Уравнение движения. | m, кг | А, м | В, м/с | С, м/с2 | D, м/с3 | Dt, мин |
| 1. | 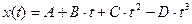 | 1,5 | 1,5 | 0,0008 | |||
| 2. | 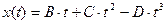 | 2,0 | - | 0,003 | |||
| 3. | 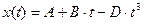 | 1,0 | - | 0,0001 | |||
| 4. | 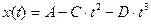 | 2,2 | -45 | - | 0,08 | ||
| 5. | 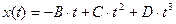 | 2,2 | - | -75 | -0,005 | ||
| 6. | 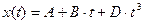 | 2,3 | - | -0,0008 | |||
| 7. | 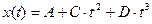 | 1,8 | - | -0.005 | |||
| 8. | 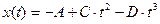 | 3,2 | -35 | - | 0,006 | ||
| 9. | 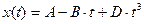 | 3,5 | -125 | - | -0.00008 | ||
| 10. | 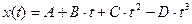 | 1,3 | 0,002 | ||||
| 11. | 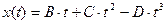 | 1,8 | - | 0,002 | |||
| 12. | 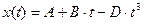 | 1,2 | - | 0,00015 | |||
| 13. | 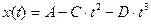 | 3,2 | - | -135 | 0,1 | ||
| 14. | 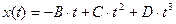 | 2,5 | - | -65 | -0,01 | ||
| 15. | 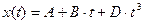 | 2,15 | - | -0,00005 | |||
| 16. | 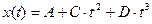 | 1,95 | - | -0.003 | |||
| 17. | 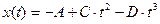 | 3,20 | -45 | - | 0,008 | ||
| 18. | 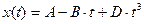 | 1,95 | -165 | - | -0,0001 |
Зависимости для построения графиков.
Таблица 2.2
| Вариант | x(t) | S(t) | u(t) | ux(t) | A(t) | N(t) |
| 1. | + | + | + | |||
| 2. | + | + | + | |||
| 3. | + | + | + | |||
| 4. | + | + | + | |||
| 5. | + | + | + | |||
| 6. | + | + | + | |||
| 7. | + | + | + | |||
| 8. | + | + | + | |||
| 9. | + | + | + | |||
| 10. | + | + | + | |||
| 11. | + | + | + | |||
| 12. | + | + | + | |||
| 13. | + | + | + | |||
| 14. | + | + | + | |||
| 15. | + | + | + | |||
| 16. | + | + | + | |||
| 17. | + | + | + | |||
| 18. | + | + | + |
Задание 3
Тема:Кинематиика материальной точки
Формулировка задания.
Две материальные точки движутся по одной прямой, совпадающей с осью Ox декартовой системы координат. Закон движения первой точки имеет вид 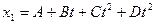 , а проекция ускорения второй точки изменяется согласно уравнению
, а проекция ускорения второй точки изменяется согласно уравнению 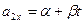 . В начальный момент времени вторая точка имела координату
. В начальный момент времени вторая точка имела координату 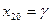 и скорость
и скорость 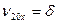 . Задания и значения параметров приведены в таблице 2.1.
. Задания и значения параметров приведены в таблице 2.1.
Размерности параметров: 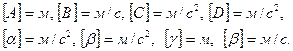
Задание 4
Тема:Кинематиика материальной точки
Формулировка задания.
Две материальные точки движутся по одной прямой, совпадающей с осью Ox декартовой системы координат. Проекция скорости первой точки изменяется по закону 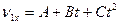 , а ускорение второй точки – по закону
, а ускорение второй точки – по закону 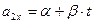 . В начальный момент времени вторая точка имела координату
. В начальный момент времени вторая точка имела координату 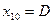 . У второй точки в начальный момент времени координата была
. У второй точки в начальный момент времени координата была 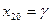 , а проекция скорости
, а проекция скорости 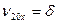 . Задания и значения параметров приведены в таблице 2.1.
. Задания и значения параметров приведены в таблице 2.1.
Размерности параметров: 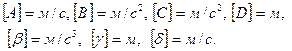
Задание 5
Тема:Кинематиика материальной точки
Формулировка задания.
Две материальные точки движутся по одной прямой, совпадающей с осью Ox декартовой системы координат. Закон движения первой точки имеет вид 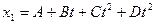 , а скорость второй точки изменяется согласно уравнению
, а скорость второй точки изменяется согласно уравнению 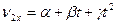 . В начальный момент времени вторая точка имела координату
. В начальный момент времени вторая точка имела координату 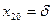 . Продолжение условия и заданные параметры приведены в таблице 3.
. Продолжение условия и заданные параметры приведены в таблице 3.
Размерности параметров: 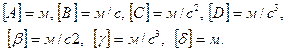
Продолжение условия и значения параметров по вариантам.
Таблица 3
| Номер задания и вариант | Задание | Значение параметров | |||||||
| A | B | C | D | a | b | g | d | ||
| 1.3. 1 | Найдите относительную скорость точек в момент совпадения их координат. | ||||||||
| .2 | Определите ускорение первой точки в тот момент, когда скорости точек станут одинаковыми. | ||||||||
| .3 | Определите расстояние между точками в тот момент, когда ускорения точек станут одинаковыми. | ||||||||
| .4 | Определите ускорение первой точки в момент ее встречи со второй. | ||||||||
| .5 | Определите расстояние между точками в тот момент, когда их скорости станут одинаковыми. | ||||||||
| .6 | Определите относительную скорость точек в тот момент, когда их ускорения станут одинаковыми. | ||||||||
| .7 | Во сколько раз будут отличаться ускорения точек в тот момент, когда скорость второй точки превысит скорость первой в два раза? | ||||||||
| .8 | Определите ускорение первой точки в тот момент, когда вторая окажется в начале координат. | ||||||||
| .9 | Определите относительную скорость точек в тот момент, когда расстояние между ними увеличится в два раза. | ||||||||
| .10 | Определите ускорение первой точки в тот момент, когда вторая остановится. | -1 | |||||||
| .11 | Определите скорость второй точки в тот момент, когда ускорение первой будет равным нулю. | -6 | |||||||
| .12 | Определите разность ускорений точек в тот момент, когда из скорости будут равны. | ||||||||
| .13 | Определите положение второй точки в тот момент, когда первая остановится. | -3 | -2 | ||||||
| .14 | Определите скорость первой точки в тот момент, когда вторая остановится. | -2 | -4 | ||||||
| 1.4.15 | Определите относительную скорость точек в тот момент, когда ускорение первой точки будет равно нулю. | -1 | -4 | -4 | -1 | ||||
| .16 | Определите ускорение первой точки в тот момент, когда скорости точек будут равны. | ||||||||
| .17 | Определите разность скоростей точек в тот момент, когда их ускорения будут равны. | -1 | |||||||
| .18 | Определите ускорение первой точки в тот момент, когда точки встретятся. | ||||||||
| .19 | Определите расстояние между точками в тот момент, когда ускорения точек станут одинаковыми. | ||||||||
| .20 | Определите ускорение первой точки в тот момент, когда вторая остановится. | -4 | -4 | ||||||
| .21 | Определите разность ускорений точек в тот момент, когда вторая точка будет двигаться быстрее первой в два раза. | ||||||||
| 1.5.22 | Определите относительную скорость точек в тот момент, когда они окажутся на расстоянии 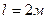 друг от друга. друг от друга. | ||||||||
| .23 | Определите разность ускорений в тот момент, когда точки встретятся. | ||||||||
| .24 | Определите координаты второй точки в тот момент, когда скорости точек будут одинаковыми. | ||||||||
| .25 | Определите расстояние между точками в тот момент, когда ускорение первой точки будет равно нулю. | -3 |
Задание 6
Тема:Динамика вращательного движения
Формулировка задания.
Момент инерции маховика, закреплённого на валу двигателя, равен 2,5 кг×м2. Уравнения изменения со временем кинематических характеристик вращающегося маховика приведены в табл.1. Угол поворота j задан в радианах, А = 0.0314 рад/с2, В = 0.1 рад/с.
Определить:
1. Мощность действующих на маховик сил в момент времени t.
2. Работу, которую может совершить маховик при торможении, если в момент времени t выключить его сцепление с двигателем.
Задание 7
Тема:Динамика вращательного движения
Формулировка задания.
Тело массой m вращается без начальной скорости вокруг своей оси. На тело действует пара сил с величиной момента M и момент сопротивления, модуль которого является функцией угловой скорости Mсопр.= f(w). Сколько оборотов сделает тело до того, как его угловая скорость станет равной w?
Значения параметров по вариантам.
Таблица 4
| Вариант | Тело | R, (l)м | m, кг | M, Дж | Mсопр | k, кг×м2 | w, рад/с |
| 1. | Полый цилиндр | 0,50 | 23,0 | 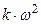 | 2,32 | 3,00 | |
| 2. | Сплошной цилиндр | 0,30 | 21,0 | 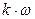 | 2,10 | 2,50 | |
| 3. | Шар | 0,45 | 23,5 | 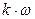 | 2,55 | 2,89 | |
| 4. | Диск | 0,75 | 21,5 | 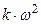 | 2,42 | 3,21 | |
| 5. | Обруч | 0,46 | 24,0 | 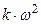 | 2,33 | 3,11 | |
| 6. | Стержень (ось проходит через середину стержня) | 0,55 | 23,7 | 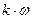 | 2,55 | 2,75 | |
| 7. | Стержень (ось проходит через конец стержня) | 0,65 | 23,4 | 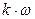 | 2,42 | 2,55 | |
| 8. | Полый цилиндр | 0,45 | 21,8 | 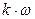 | 2,22 | 3,05 | |
| 9. | Шар | 0,55 | 24,3 | 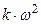 | 2,65 | 3,19 | |
| 10. | Обруч | 0,58 | 23,0 | 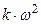 | 2,53 | 3,56 | |
| 11. | Полый цилиндр | 0,45 | 22,5 | 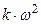 | 2,12 | 3,10 | |
| 12. | Сплошной цилиндр | 0,35 | 21,5 | 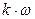 | 2,15 | 2,50 | |
| 13. | Стержень (ось проходит через середину стержня) | 0,55 | 22,7 | 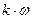 | 2,55 | 3,05 | |
| 14. | Стержень (ось проходит через конец стержня) | 0,65 | 23,4 | 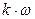 | 2,42 | 2,55 | |
| 15. | Полый цилиндр | 0,45 | 21,9 | 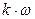 | 2,52 | 3,05 | |
| 16. | Шар | 0,35 | 24,3 | 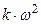 | 3,55 | 3,19 | |
| 17. | Обруч | 0,58 | 23,0 | 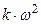 | 2,53 | 3,56 | |
| 18. | Шар | 0,48 | 25,5 | 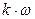 | 2,35 | 2,85 | |
| 19. | Шар | 0,48 | 25,5 | 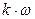 | 2,35 | 2,85 | |
| 20. | Диск | 0,75 | 22,5 | 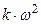 | 2,32 | 2,81 | |
| 21. | Обруч | 0,46 | 24,0 | 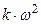 | 2,33 | 3,21 | |
| 22. | Стержень (ось проходит через конец стержня) | 0,65 | 23,4 | 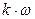 | 2,42 | 2,55 | |
| 23. | Полый цилиндр | 0,45 | 21,9 | 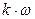 | 2,52 | 3,05 | |
| 24. | Шар | 0,45 | 24,3 | 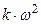 | 3,35 | 3,29 | |
| 25. | Стержень (ось проходит через конец стержня) | 0,65 | 21,4 | 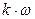 | 2,32 | 2,55 | |
| 26. | Обруч | 0,56 | 24,5 | 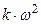 | 2,35 | 3,15 |
Задание 8
Тема: Вязкость.
Формулировка задания.
Шар радиусом R и массой m и плотностью rт без начальной скорости погружается в среде, плотность которой r.Найти закон движения шара, считая, что сила сопротивления жидкости является функцией скорости погружения т.е.
Fc =f(v). Максимальная скорость шара Vмах. Определить константу k. Построить график зависимости скорости от времени v= f(t)
Значение параметров по вариантам
Таблица 5
| Вариант | Параметр Материал шара | R | f(v) | rт | Vмах | r |
| мм | Н | кг/м3 | м/с | кг/м3 | ||
| Медь | k v 2 | 0,3/с. | ||||
| Свинец | 2. | k v | 0,4м/с | |||
| Алюминий | 2.5 | k v 2 | 0,5 м/с | |||
| Железо | k v | 0,1 м/с | ||||
| Платина | 1.5 | k v 2 | 0,05 м/с |
