Положение прямой линии относительно плоскостей проекций

В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.3.4).

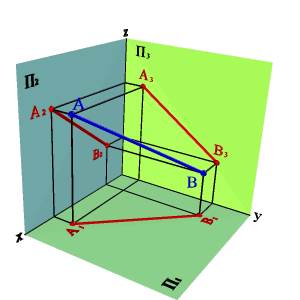
А) модель

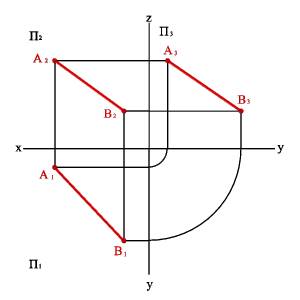
Б) эпюр

Рисунок 3.4. Прямая общего положения

2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:

2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.3.5). Для любой пары точек горизонтали должно быть справедливо равенство

zA=zB Þ A2B2//0x;

A3B3//0y Þ xA–xB#0,

yA–yB#0, zA–zB=0.

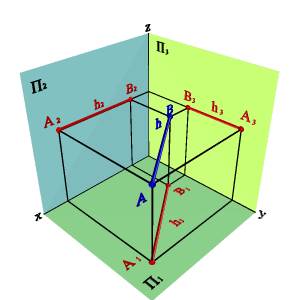
А) модель

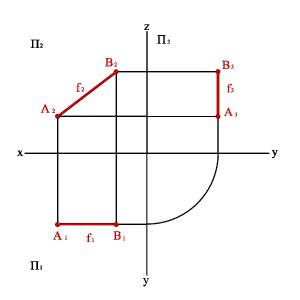
Б) эпюр

Рисунок 3.8. Фронтально проецирующая прямая

3.3. Горизонтально проецирующая прямая - АВ (рис.3.10)

xА–xВ=0ü

yА–yВ=0ý

ZА–zВ#0þ.

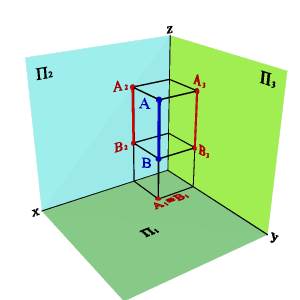
А) модель

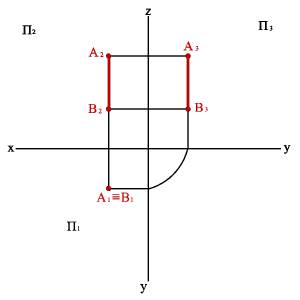
Б) эпюр

Рисунок 3.10. Горизонтально-проецирующая прямая

4. Прямые параллельные биссекторным плоскостям (рис. 3.11)

АВ //S1бис Þ xA–xB=0;

zB–zA=yB–yA;

СD//S2бис Þ xС–xD=0; zD–zC=yC–yD.

Биссекторной плоскостью называется плоскость проходящая через ось 0х и делящая двухгранный угол между плоскостями проекций П₁ и П₂ пополам. Биссекторная плоскость проходящая через 1 и 3 четверти называется первой биссекторной плоскостью (S₁бис) ,а через 2 и 4 четверти - второй (S₂бис).

5. Прямые перпендикулярные биссекторным плоскостям (рис. 3.11)

АВ^S2бис Þ xA–xB=0;

zB–zA=yВ–yА;.

СD^S1бис Þ xС–xD=0;

zD–zC=yC–yD

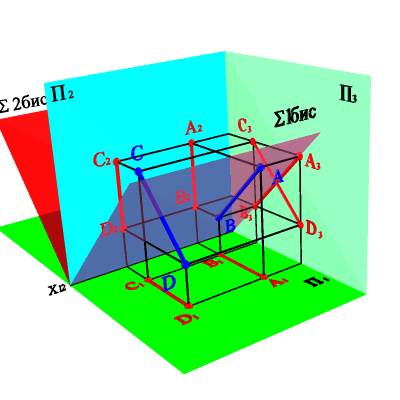
А) модель

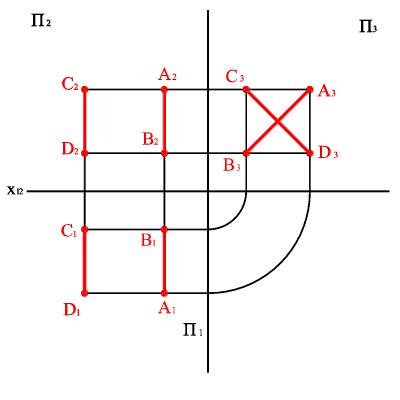
Б) эпюр

Рисунок 3.11. Прямые параллельные и перпендикулярные биссекторным плоскостям

Следы прямой линии.

Следом прямой линии называется точка (рис. 3.12),

в которой прямая пересекается с плоскостью проекций (так как след принадлежит одной из плоскостей проекций то его одна координата должна быть равна нулю).

Горизонтальный след - М (ZM=0) - точка пересечения прямой с горизонтальной плоскостью проекций.

Фронтальный след - N (YN=0) - точка пересечения прямой с фронтальной плоскостью проекций.

Профильный след - Т (XТ=0) - точка пересечения прямой с профильной плоскостью проекций.

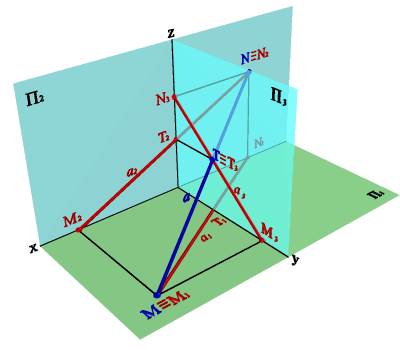
А) модель

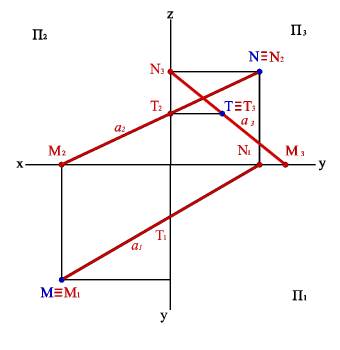
Б) эпюр

Рисунок 3.12.Следы прямой линии в системе трех плоскостей проекций

Следы прямой являются точками частного положения. Одноименные проекции следа прямой совпадают с самим следом, а другие проекции лежат на осях. Например, фронтальный след прямой N2 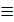N, а N1 лежит на оси x, N3 - на оси z. Отмеченные особенности в расположении следов проекций позволяет сформулировать следующие правила:

1. Для построения горизонтального следа М прямой необходимо продолжить ее фронтальную проекцию до пересечения с осью 0x и в этой точке восстановить перпендикуляр к оси до пересечения с горизонтальной проекцией прямой.

2. Для построения фронтального следа N прямой нужно из точки пересечения горизонтальной проекции её с осью 0x восстановить перпендикуляр до пересечения с фронтальной проекцией прямой.

С помощью этих правил найдены на эпюре следы прямой а (рис.3.13) . Здесь же показаны совпавшие проекции точки А принадлежащей рассматриваемой прямой. Особенность этой точки в том, что она равноудалена от плоскостей проекций, то есть находятся в биссекторной плоскости S₂бис.

Следы прямой, являются точками, в которых прямая переходит из одного октанта в другой, позволяют отмечать её видимость. Видимой частью прямой будет та, которая расположена в пределах первого октанта.

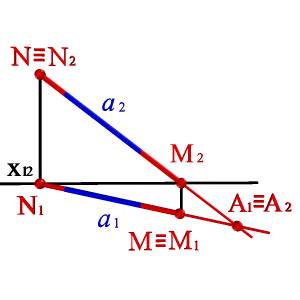
Рисунок 3.13 Нахождение горизонтального и фронтального следов прямой линии