Матрицаның дәрежелері
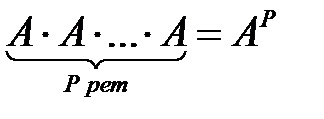 .
. 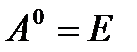 деп келісейік.
деп келісейік. 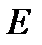 – бірлік матрица; Егер
– бірлік матрица; Егер 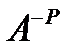 ерекше емес болса, онда
ерекше емес болса, онда 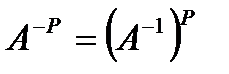 . 1)
. 1) 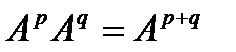 . 2)
. 2) 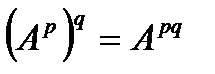 .
.
Квадрат емес матрицаны дәрежеге шығаруға болмайды! Егер 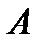 және
және 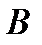 реті бірдей матрицалар және
реті бірдей матрицалар және 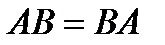 болса, онда
болса, онда 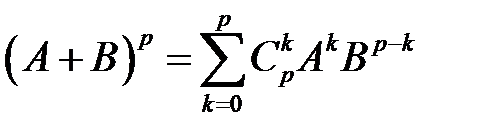 .
.
3. 4. Сызықты теңдеулер жүйесін шешудің әдістері. Гаусс әдісі (басты элементтер әдісі).
САТЖ шешу әдістерін негізгі екі топқа бөлуге болады: 1. Дәл әдістері – жүйе шешімін есептеудің ақырлы алгоритмдерін береді (Крамер, Гаусс, негізгі элементтер, квадрат түбірлер т.б. әдістері). 2. Итерациялық әдістер – берілген дәлдікпен жинақталатын шексіз процесстер арқылы жүйе шешімін алуға мүмкіндік береді (итерация, Зейдель, релаксация т.б. әдістері).
Дөңгелектеу нәтижесінде дәл әдістердің де нәтижелері жуық болуы мүмкін, оның үстіне, жалпы жағдайда, түбір қателігінің бағасын алу қиындық тудырады. Ал итерациялық процесстерді қолданғанда тағы әдіс қателігі қосылады. Итерациялық әдістерді тиімді пайдалану бастапқы жуықтауды таңдауға және процесс жинақтылығының тездігіне байланысты екенін байқаймыз.
Гаусс әдісі. Белгісіздерді біртіндеп жою алгоритмі
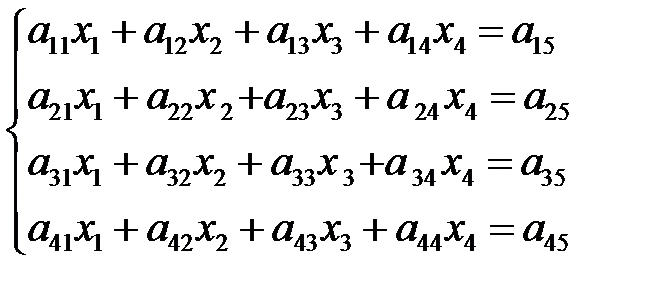 (1)
(1)
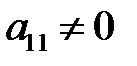 (негізгі элемент) болсын. (1) жүйенің бірінші теңдеуінің коэффициенттерін
(негізгі элемент) болсын. (1) жүйенің бірінші теңдеуінің коэффициенттерін 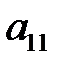 -ге бөліп, алатынымыз:
-ге бөліп, алатынымыз:
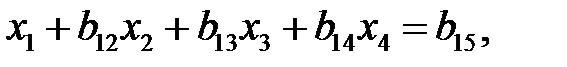 (2)
(2)
мұндағы, 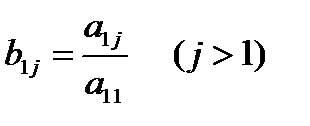 .
.
(2) теңдеуді қолданып, (1) жүйеден 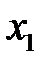 -ді жоюға болады. Бұл үшін (1) жүйенің екінші теңдеуінен
-ді жоюға болады. Бұл үшін (1) жүйенің екінші теңдеуінен 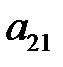 -ге көбейтілген (2) теңдеуді, (1) жүйенің үшінші теңдеуінен
-ге көбейтілген (2) теңдеуді, (1) жүйенің үшінші теңдеуінен 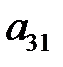 -ге көбейтілген (2) теңдеуді, т.с.с. алып тастаймыз. Нәтижесінде үш теңдеуден тұратын жүйе аламыз:
-ге көбейтілген (2) теңдеуді, т.с.с. алып тастаймыз. Нәтижесінде үш теңдеуден тұратын жүйе аламыз:
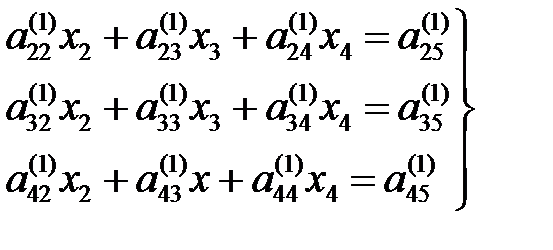 (1/)
(1/)
мұндағы 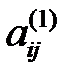
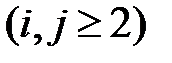 коэффициенттері
коэффициенттері 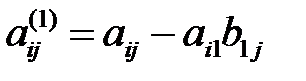
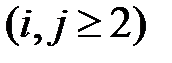 формуласымен есептеледі.
формуласымен есептеледі.
(1/) жүйенің бірінші теңдеуінің коэфициенттерін 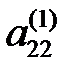 – негізгі элементке бөліп, келесі теңдеуді аламыз:
– негізгі элементке бөліп, келесі теңдеуді аламыз:
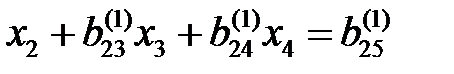 , (2/)
, (2/)
мұндағы 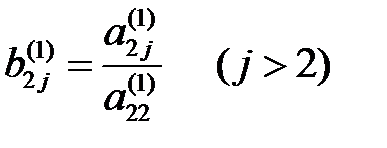 .
.
Енді 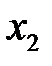 -ні
-ні 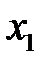 -ді жойғандағыдай жойып, келесі теңдеулер жүйесіне келеміз:
-ді жойғандағыдай жойып, келесі теңдеулер жүйесіне келеміз:
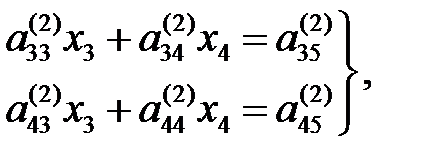 (1//)
(1//)
мұндағы 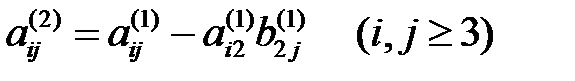 .
.
(1//) жүйенің бірінші теңдеуінің коэффициенттерін 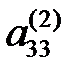 – негізгі элементке бөліп, аламыз:
– негізгі элементке бөліп, аламыз:
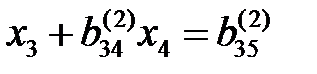 , (2//)
, (2//)
мұндағы 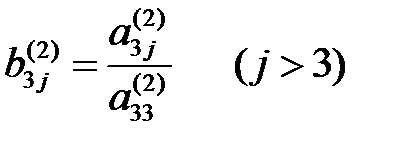 .
.
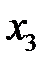 -ті жоғарғыдағыдай (1//) жүйеден жойып, алатынымыз:
-ті жоғарғыдағыдай (1//) жүйеден жойып, алатынымыз:
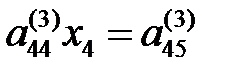 , (1///)
, (1///)
мұндағы 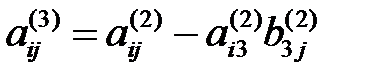
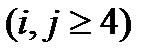 .
.
Бұдан
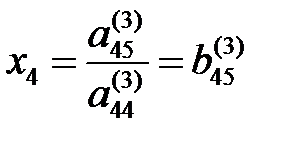 . (2///)
. (2///)
Қалған белгісіздер (2/), (2//) және (2) теңдеулерден біртіндеп анықталады.
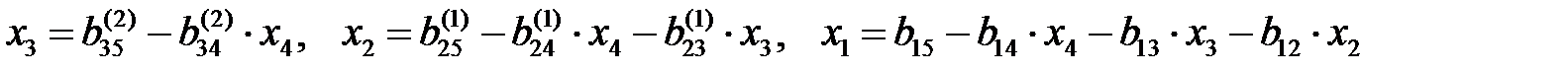
Сонымен, сызықты жүйені Гаусс әдісімен шешу процессі үшбұрышты матрицалы (2), (2/), (2//), (2///) эквивалентті жүйені құруға әкеледі. Әдісті қолданудың қажетті және жеткілікті шарты барлық «негізгі элементтерінің» нөлден өзгешелігі.
Зейдель әдісі
Ең қарапайым итерациялық әдістердің бірі – Гаусс-Зейдель әдісі болып табылады. Осы әдісті пайдаланып жүйені шешуге мысал келтірейік.
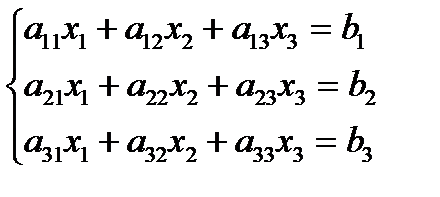 (1)
(1)
Айталық жүйенің диагоналдық 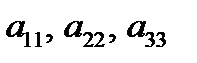 элементтері нөлден өзгеше болсын (егер болмаса, теңдеулердің орындарын алмастырамыз). Жүйенің бірінші, екінші және үшінші теңдеулерінен сәйкесінше
элементтері нөлден өзгеше болсын (егер болмаса, теңдеулердің орындарын алмастырамыз). Жүйенің бірінші, екінші және үшінші теңдеулерінен сәйкесінше 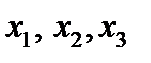 белгісіздерін өрнектейміз:
белгісіздерін өрнектейміз:
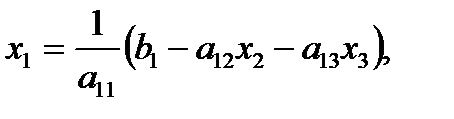 (2)
(2)
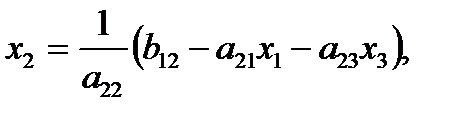 (.3)
(.3)
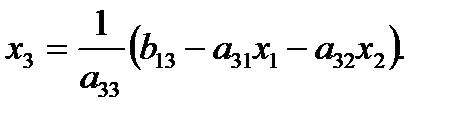 (.4)
(.4)
Белгісіздерге бастапқы (нөлдік) жуықтаулар берейік: 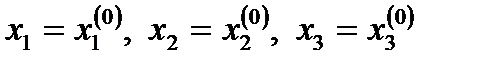 . Осы мәндерді (2) өрнегінің оң жақ бөлігіне қоя отырып,
. Осы мәндерді (2) өрнегінің оң жақ бөлігіне қоя отырып, 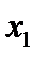 үшін жаңа (бірінші) жуықтауды аламыз:
үшін жаңа (бірінші) жуықтауды аламыз:
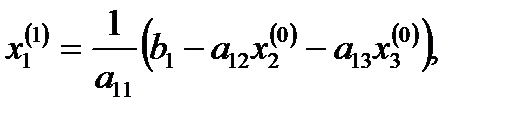
Осы мәнді 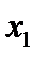 үшін және
үшін және 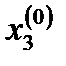 жуықтауын
жуықтауын 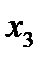 үшін пайдаланып, (3) өрнегінен
үшін пайдаланып, (3) өрнегінен 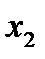 үшін бірінші жуықтауды табамыз:
үшін бірінші жуықтауды табамыз:
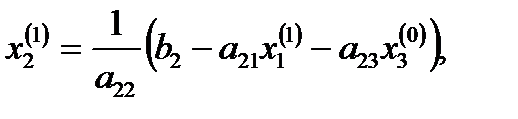
Соңында, есептелген 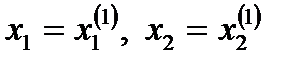 мәндерін пайдаланып, (4) өрнегінің көмегімен
мәндерін пайдаланып, (4) өрнегінің көмегімен 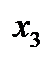 үшін бірінші жуықтауын табамыз:
үшін бірінші жуықтауын табамыз:
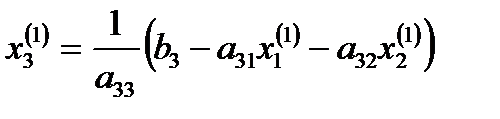 .
.
Осымен (2) – (4) жүйелерді шешудің бірінші итерациясы аяқталады. Енді 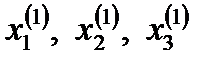 мәндерін пайдаланып, осындай тәсілмен екінші итерацияны жүргіземіз, нәтижесінде екінші жуықтау табылады:
мәндерін пайдаланып, осындай тәсілмен екінші итерацияны жүргіземіз, нәтижесінде екінші жуықтау табылады: 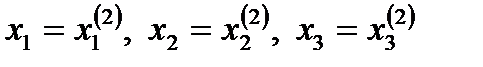 және тағы басқалары.
және тағы басқалары.  номерлі жуықтауды мынадай түрде көрсетуге болады:
номерлі жуықтауды мынадай түрде көрсетуге болады:
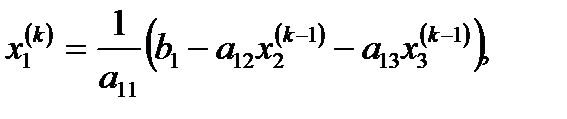
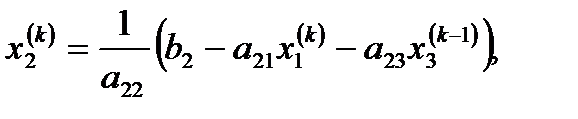
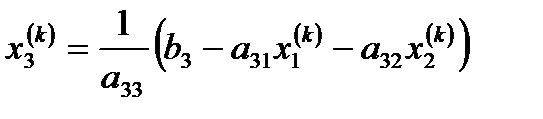 .
.
Итерациялық үрдіс 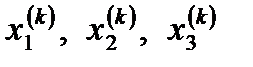 мәндері берілген дәлдікпен
мәндері берілген дәлдікпен 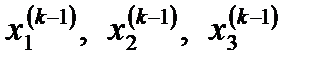 мәндеріне жақындағанша жалғастырылады.
мәндеріне жақындағанша жалғастырылады.
