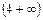| № п/п | Примеры ПП 16 9. Текстовые задачи разного содержания на нахождение наибольшего и наименьшего значения величин |
| №24 | 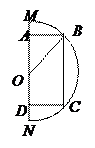 Площадь поверхности сферы равна Площадь поверхности сферы равна 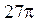 . Какова высота цилиндра наибольшего объема, вписанного в эту сферу? Обозначим высоту цилиндра . Какова высота цилиндра наибольшего объема, вписанного в эту сферу? Обозначим высоту цилиндра 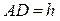 , , 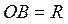 . По условию . По условию 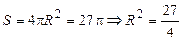 , , 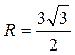 . Из . Из 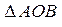 : : 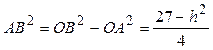 . Объем цилиндра . Объем цилиндра 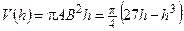 . По смыслу задачи . По смыслу задачи 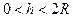 , т.е. , т.е. 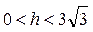 . Исследуем функцию . Исследуем функцию 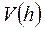 на этом интервале. Производная на этом интервале. Производная 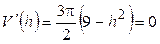 при при 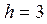 , вблизи этого значения , вблизи этого значения 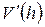 меняет знак с + на –, значит при этой высоте объем цилиндра будет наибольшим. меняет знак с + на –, значит при этой высоте объем цилиндра будет наибольшим. |
| №25 | Владелец фабрики установил, что если он будет продавать свои изделия по цене 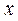 руб., то его годовая прибыль руб., то его годовая прибыль 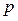 составит составит 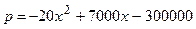 руб. Определите руб. Определите 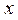 , при котором прибыль будет максимальной. , при котором прибыль будет максимальной. 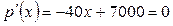 при при 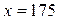 , при этой цене прибыль будет максимальной. , при этой цене прибыль будет максимальной. |
| пп 16. I. исследование функций |
| № п/п | ЗАДАЧИ |
| ПП16.I №1 | Найдите интервалы монотонности и точки экстремума функции 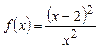 . РЕШЕНИЕ: Функция . РЕШЕНИЕ: Функция 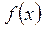 не определена при не определена при 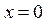 . . 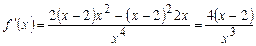 , , 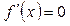 при при 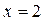 . . Функция 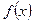 возрастает при возрастает при 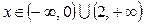 ; убывает при ; убывает при 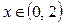 ; ; 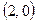 – точка минимума. – точка минимума. |
| ПП16.I №2 | Найдите экстремумы функции 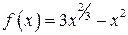 . . 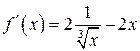 , , 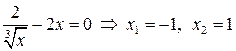 , , 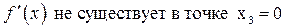 . . 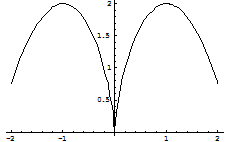
Вид графика функции 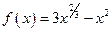 . . |
| ПП16.I №3 | Исследуйте функцию 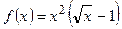 на возрастание (убывание) и экстремумы. на возрастание (убывание) и экстремумы. 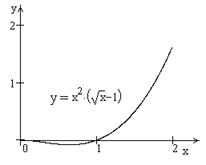 РЕШЕНИЕ: Функция РЕШЕНИЕ: Функция 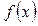 определена для определена для 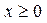 . Производная функции . Производная функции 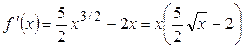 обращается в ноль при обращается в ноль при 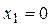 и и 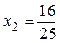 , , 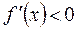 при при 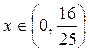 , , 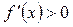 при при 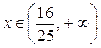 , то есть в точке , то есть в точке 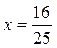 функция принимает минимальное значение. функция принимает минимальное значение. |
| ПП16.I №4 | Исследуйте функцию 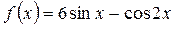 на возрастание (убывание) и экстремумы. РЕШЕНИЕ: Производная функции на возрастание (убывание) и экстремумы. РЕШЕНИЕ: Производная функции 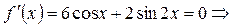 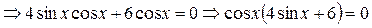 . . 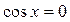 при при 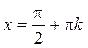 , второй множитель положителен при любых , второй множитель положителен при любых 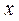 . Знак производной совпадает со знаком . Знак производной совпадает со знаком 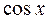 : при : при 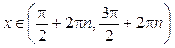 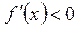 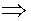 функция убывает; при функция убывает; при 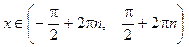 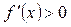 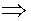 функция возрастает, в точках функция возрастает, в точках 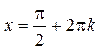 достигается максимальное достигается максимальное 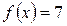 , а в точках , а в точках 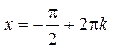 – минимальное – минимальное 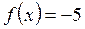 значения функции значения функции 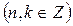 . . |
| ПП16.I №5 | Исследуйте функцию 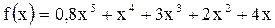 на возрастание (убывание) и экстремумы. РЕШЕНИЕ: Производная функции представляет собой многочлен, который мы преобразуем следующим образом: на возрастание (убывание) и экстремумы. РЕШЕНИЕ: Производная функции представляет собой многочлен, который мы преобразуем следующим образом: 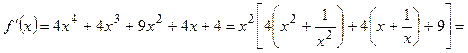 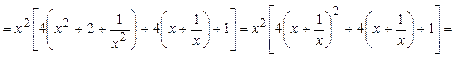 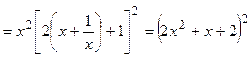 , откуда видно, что , откуда видно, что 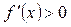 при любых при любых 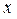 , значит, функция возрастает для всех , значит, функция возрастает для всех 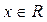 и экстремумов не имеет. и экстремумов не имеет. |
| ПП16.I №6 | Исследуйте функцию 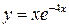 и постройте её график. РЕШЕНИЕ: 1) и постройте её график. РЕШЕНИЕ: 1) 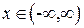 , , 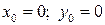 - точка пересечения с осями. 2) f (x) – непрерывна всюду - точка пересечения с осями. 2) f (x) – непрерывна всюду 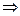 вертикальных асимптот нет. вертикальных асимптот нет. 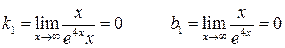 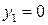 - наклонная (горизонтальная) асимптота при - наклонная (горизонтальная) асимптота при 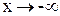 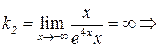 наклонных асимптот при наклонных асимптот при 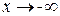 нет. 3) нет. 3) 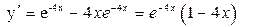 , , 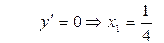 . 4) . 4) 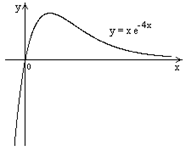 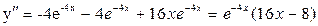 , , 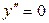 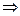 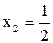 . . | х | 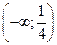 | 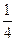 | 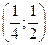 | 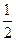 | 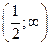 | | у | 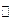 | 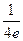 | 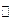 |  |  | 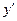 | + | | – | – | – | 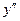 | – | – | – | | + | | |  | max |  | перегиб |  | Вид графика функции 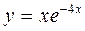 . . |
| ПП16.I №7 | Сколько раз график функции 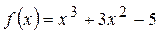 пересекает ось пересекает ось 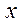 ? РЕШЕНИЕ: Функция определена для всех ? РЕШЕНИЕ: Функция определена для всех 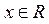 , не обладает определенной четностью, непериодическая. , не обладает определенной четностью, непериодическая. 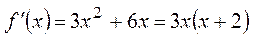 ; ; 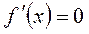 при при 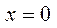 и и 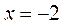 . График функции . График функции 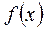 пересекает ось пересекает ось 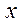 в одной точке в одной точке 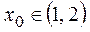 . Построим схему. . Построим схему. 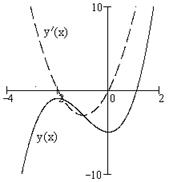 |
| ПП16.I №8 | Исследуйте функцию 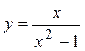 и постройте её график. РЕШЕНИЕ: 1) Область определения функции: и постройте её график. РЕШЕНИЕ: 1) Область определения функции: 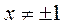 ; эти точки являются точками разрыва функции; при ; эти точки являются точками разрыва функции; при 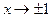 функция функция 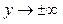 ; при ; при 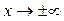 , , 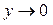 . . 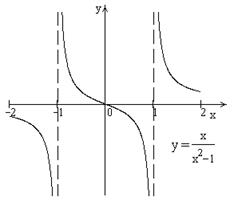 2) Функция нечетная: 2) Функция нечетная: 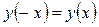 . Построим график для . Построим график для 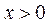 и отобразим его нечетным образом относительно начала координат. 3) Точка пересечения с осью и отобразим его нечетным образом относительно начала координат. 3) Точка пересечения с осью 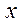 определяется условием определяется условием 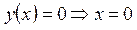 , , 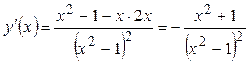 , , 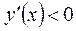 для всех для всех 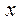 из области определения, т.е. функция является убывающей и не имеет экстремумов. из области определения, т.е. функция является убывающей и не имеет экстремумов. |
| ПП16.I №9 | Исследуйте функцию 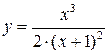 и постройте её график. РЕШЕНИЕ: 1) Функция определена всюду, кроме точки и постройте её график. РЕШЕНИЕ: 1) Функция определена всюду, кроме точки 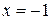 . График функции имеет вертикальную асимптоту . График функции имеет вертикальную асимптоту 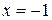 . 2) Точка пересечения с осями: . 2) Точка пересечения с осями: 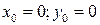 . 3) Выясним, существуют ли наклонные асимптоты. Вычислим пределы: . 3) Выясним, существуют ли наклонные асимптоты. Вычислим пределы: 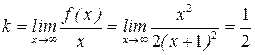 ; ; 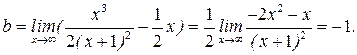 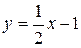 является наклонной асимптотой. 4) Находим производную: является наклонной асимптотой. 4) Находим производную: 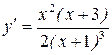 . Знак производной определяется знаком дроби . Знак производной определяется знаком дроби 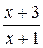 . При . При 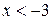 и и 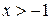 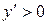 , а при , а при 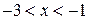 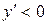 . Интервалы возрастания есть . Интервалы возрастания есть 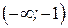 и и 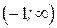 ; интервал убывания ; интервал убывания 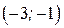 . В области определения функции производная существует всюду и обращается в ноль при . В области определения функции производная существует всюду и обращается в ноль при 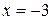 и и  . При . При 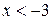 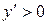 , а при , а при 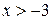 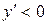 . Следовательно, точка . Следовательно, точка 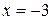 является точкой максимума. Находим значение функции при является точкой максимума. Находим значение функции при 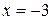 : : 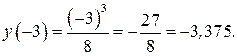 При переходе через другую критическую точку При переходе через другую критическую точку  производная знак не меняет, т.е. производная знак не меняет, т.е.  не является точкой экстремума. 5) Находим вторую производную не является точкой экстремума. 5) Находим вторую производную 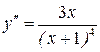 . Видим, что . Видим, что 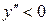 при при 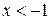 , интервал , интервал 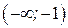 является областью выпуклости. является областью выпуклости. 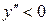 также при также при 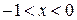 - это тоже область выпуклости; - это тоже область выпуклости; 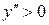 при при 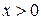 - это область вогнутости. В области определения функции - это область вогнутости. В области определения функции 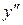 существует всюду; существует всюду; 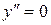 при при  . Так как при переходе через эту точку . Так как при переходе через эту точку 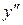 меняет знак, то меняет знак, то  есть абсцисса точки перегиба. Находим есть абсцисса точки перегиба. Находим 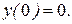 | х | 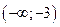 | 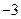 | 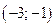 | 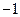 | 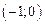 | 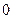 | 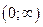 | | у | 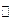 | 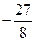 | 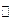 | 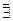 | 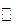 | | 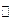 | 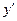 | + | | – | 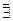 | + | | + | 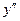 | – | – | – |  | – | | + | | |  | max |  | |  | перегиб | 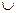 | График 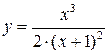 имеет вид имеет вид 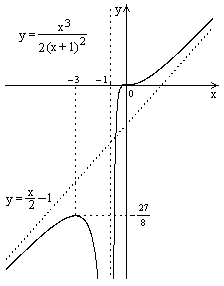 |
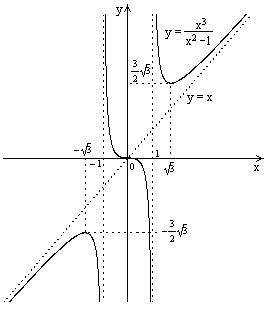
| ПП16.I №10 | Исследуйте функцию 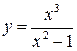 и постройте её график. РЕШЕНИЕ: 1). Функция определена всюду, кроме точек и постройте её график. РЕШЕНИЕ: 1). Функция определена всюду, кроме точек 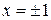 . Точки пересечения графика с координатными осями: . Точки пересечения графика с координатными осями: 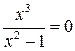 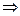 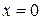 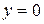 - точка пересечения с осями. 2). Функция нечетная, - точка пересечения с осями. 2). Функция нечетная, 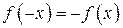 , график симметричен относительно начала координат, достаточно исследовать функцию при , график симметричен относительно начала координат, достаточно исследовать функцию при 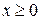 . 3). Точка . 3). Точка 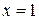 является точкой разрыва II-рода, график функции имеет вертикальную асимптоту является точкой разрыва II-рода, график функции имеет вертикальную асимптоту 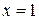 , , 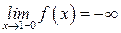 , , 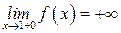 . Выясним, существуют ли наклонные асимптоты. Вычислим пределы: . Выясним, существуют ли наклонные асимптоты. Вычислим пределы: 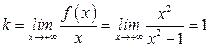 ; ; 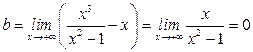 , т.е., , т.е., 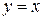 является правой наклонной асимптотой (и левой, так как при операции симметрии прямая переходит сама в себя). 4). Находим производную: является правой наклонной асимптотой (и левой, так как при операции симметрии прямая переходит сама в себя). 4). Находим производную: 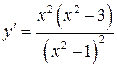 . Знак производной определяется знаком . Знак производной определяется знаком 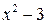 . При . При 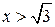 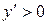 , а при , а при 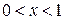 и и 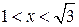 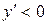 . Интервал возрастания - . Интервал возрастания - 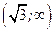 ; интервалы убывания - ; интервалы убывания - 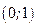 и и 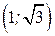 . В области определения функции производная обращается в нуль при . В области определения функции производная обращается в нуль при  и и 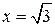 . При . При 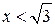 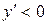 , а при , а при 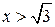 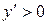 . Следовательно, точка . Следовательно, точка 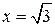 является точкой минимума. Находим значение функции при является точкой минимума. Находим значение функции при 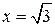 : : 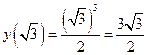 . При переходе через критическую точку . При переходе через критическую точку  производная знак не меняет, т.е. производная знак не меняет, т.е.  не является точкой экстремума. 5). Находим вторую производную не является точкой экстремума. 5). Находим вторую производную 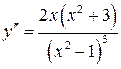 . Видим, что . Видим, что 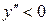 при при 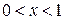 , на интервале , на интервале 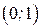 график функции выпуклый вверх. При график функции выпуклый вверх. При 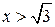 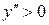 - график функции выпуклый вниз. В области определения функции - график функции выпуклый вниз. В области определения функции 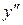 существует всюду; существует всюду; 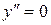 при при  . Так как при переходе через эту точку . Так как при переходе через эту точку 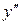 меняет знак, то меняет знак, то  есть абсцисса точки перегиба. Находим есть абсцисса точки перегиба. Находим 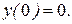 | х | 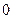 | 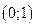 | 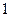 | 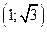 | 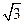 | 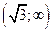 | | у | 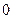 | 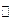 | 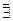 | 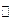 | 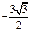 |  | 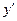 | 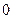 | – | 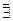 | – | 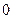 | – | 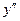 | 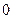 | – | 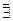 | + | + | + | | | перегиб | 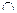 | | 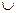 | min | 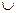 | График 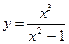 имеет вид: имеет вид:
|
| ПП16.I №11 | Исследуйте функцию 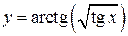 и постройте её график. РЕШЕНИЕ: 1). Так как функция периодична с основным периодом и постройте её график. РЕШЕНИЕ: 1). Так как функция периодична с основным периодом 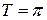 , достаточно исследовать ее поведение на промежутке, длиной равном периоду, например, на , достаточно исследовать ее поведение на промежутке, длиной равном периоду, например, на 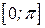 . Арктангенс определен для всех значений аргумента, поэтому областью определения сложной функции . Арктангенс определен для всех значений аргумента, поэтому областью определения сложной функции 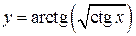 будут промежутки оси будут промежутки оси 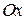 , на которых , на которых 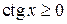 , т.е., для промежутка , т.е., для промежутка 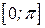 это будет это будет 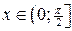 . Для . Для 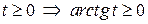 , область значений , область значений 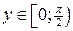 . Точки пересечения графика с координатными осями: при . Точки пересечения графика с координатными осями: при 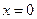 котангенс не определен, точек пересечения с осью котангенс не определен, точек пересечения с осью 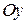 нет. Точки пересечения с осью нет. Точки пересечения с осью 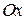 находим, решая уравнение находим, решая уравнение 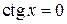 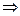 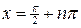 . 2). Четностью или нечетностью функция не обладает. 3). Точка . 2). Четностью или нечетностью функция не обладает. 3). Точка 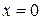 не является точкой разрыва, так как не является точкой разрыва, так как 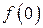 не определена, не определена, 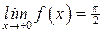 . Поскольку на каждом периоде график . Поскольку на каждом периоде график 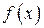 лежит в конечной области плоскости лежит в конечной области плоскости 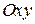 , асимптот у графика существовать не может. 4). Найдем производную: , асимптот у графика существовать не может. 4). Найдем производную: 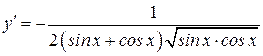 . Для . Для 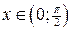 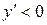 , , 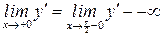 , т.е., на каждом отдельном промежутке области определения функция монотонно убывает. 5). , т.е., на каждом отдельном промежутке области определения функция монотонно убывает. 5). 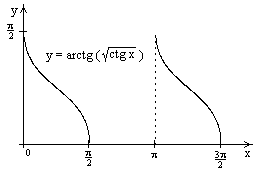 Найдем вторую производную Найдем вторую производную 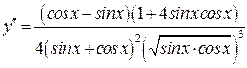 . Корень уравнения . Корень уравнения 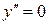 на на 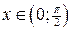 - - 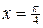 . При . При 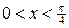 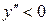 график функции выпуклый вниз, при график функции выпуклый вниз, при 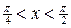 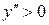 - график функции выпуклый вверх. Точка графика - график функции выпуклый вверх. Точка графика 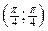 - точка перегиба. График - точка перегиба. График 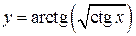 имеет вид имеет вид |
| ПП16.I №12 | Постройте график функции 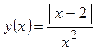 . Область определения функции: . Область определения функции: 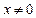 , это точка бесконечного разрыва функции, , это точка бесконечного разрыва функции, 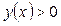 для всех для всех 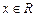 ; ; 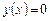 при при 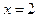 ; ; 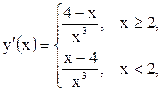 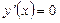 при при 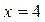 . . 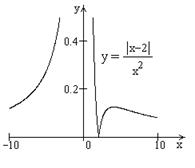 Построим схему. Построим схему. |
Наши рекомендации
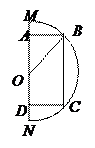 Площадь поверхности сферы равна
Площадь поверхности сферы равна 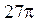 . Какова высота цилиндра наибольшего объема, вписанного в эту сферу? Обозначим высоту цилиндра
. Какова высота цилиндра наибольшего объема, вписанного в эту сферу? Обозначим высоту цилиндра 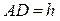 ,
, 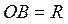 . По условию
. По условию 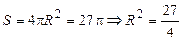 ,
, 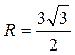 . Из
. Из 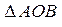 :
: 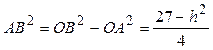 . Объем цилиндра
. Объем цилиндра 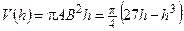 . По смыслу задачи
. По смыслу задачи 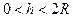 , т.е.
, т.е. 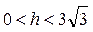 . Исследуем функцию
. Исследуем функцию 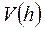 на этом интервале. Производная
на этом интервале. Производная 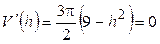 при
при 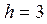 , вблизи этого значения
, вблизи этого значения 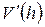 меняет знак с + на –, значит при этой высоте объем цилиндра будет наибольшим.
меняет знак с + на –, значит при этой высоте объем цилиндра будет наибольшим. 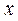 руб., то его годовая прибыль
руб., то его годовая прибыль 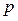 составит
составит 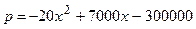 руб. Определите
руб. Определите 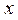 , при котором прибыль будет максимальной.
, при котором прибыль будет максимальной. 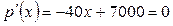 при
при 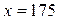 , при этой цене прибыль будет максимальной.
, при этой цене прибыль будет максимальной. 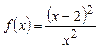 . РЕШЕНИЕ: Функция
. РЕШЕНИЕ: Функция 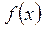 не определена при
не определена при 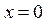 .
. 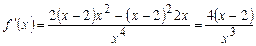 ,
, 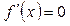 при
при 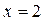 .
. 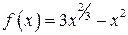 .
. 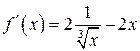 ,
, 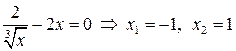 ,
, 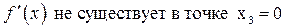 .
. 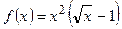 на возрастание (убывание) и экстремумы.
на возрастание (убывание) и экстремумы.  РЕШЕНИЕ: Функция
РЕШЕНИЕ: Функция 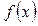 определена для
определена для 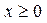 . Производная функции
. Производная функции 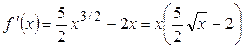 обращается в ноль при
обращается в ноль при 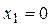 и
и 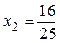 ,
, 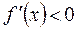 при
при 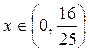 ,
, 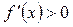 при
при 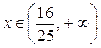 , то есть в точке
, то есть в точке 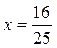 функция принимает минимальное значение.
функция принимает минимальное значение. 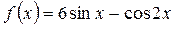 на возрастание (убывание) и экстремумы. РЕШЕНИЕ: Производная функции
на возрастание (убывание) и экстремумы. РЕШЕНИЕ: Производная функции 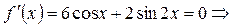
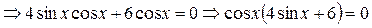 .
. 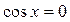 при
при 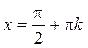 , второй множитель положителен при любых
, второй множитель положителен при любых 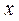 . Знак производной совпадает со знаком
. Знак производной совпадает со знаком 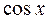 : при
: при 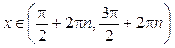
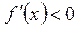
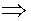 функция убывает; при
функция убывает; при 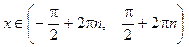
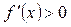
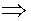 функция возрастает, в точках
функция возрастает, в точках 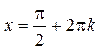 достигается максимальное
достигается максимальное 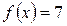 , а в точках
, а в точках 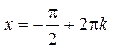 – минимальное
– минимальное 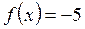 значения функции
значения функции 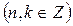 .
. 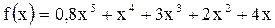 на возрастание (убывание) и экстремумы. РЕШЕНИЕ: Производная функции представляет собой многочлен, который мы преобразуем следующим образом:
на возрастание (убывание) и экстремумы. РЕШЕНИЕ: Производная функции представляет собой многочлен, который мы преобразуем следующим образом: 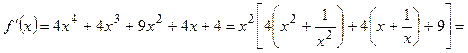
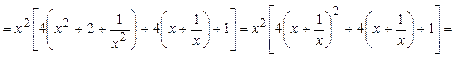
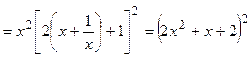 , откуда видно, что
, откуда видно, что 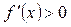 при любых
при любых 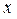 , значит, функция возрастает для всех
, значит, функция возрастает для всех 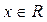 и экстремумов не имеет.
и экстремумов не имеет. 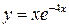 и постройте её график. РЕШЕНИЕ: 1)
и постройте её график. РЕШЕНИЕ: 1) 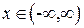 ,
, 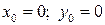 - точка пересечения с осями. 2) f (x) – непрерывна всюду
- точка пересечения с осями. 2) f (x) – непрерывна всюду 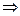 вертикальных асимптот нет.
вертикальных асимптот нет. 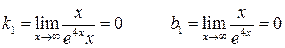
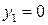 - наклонная (горизонтальная) асимптота при
- наклонная (горизонтальная) асимптота при 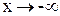
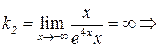 наклонных асимптот при
наклонных асимптот при 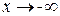 нет. 3)
нет. 3) 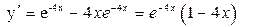 ,
, 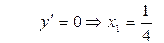 . 4)
. 4) 
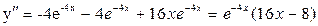 ,
, 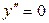
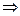
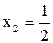 .
. 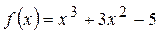 пересекает ось
пересекает ось 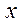 ? РЕШЕНИЕ: Функция определена для всех
? РЕШЕНИЕ: Функция определена для всех 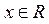 , не обладает определенной четностью, непериодическая.
, не обладает определенной четностью, непериодическая. 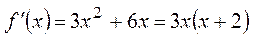 ;
; 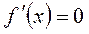 при
при 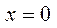 и
и 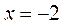 . График функции
. График функции 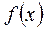 пересекает ось
пересекает ось 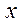 в одной точке
в одной точке 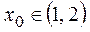 . Построим схему.
. Построим схему. 
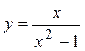 и постройте её график. РЕШЕНИЕ: 1) Область определения функции:
и постройте её график. РЕШЕНИЕ: 1) Область определения функции: 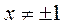 ; эти точки являются точками разрыва функции; при
; эти точки являются точками разрыва функции; при 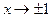 функция
функция 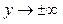 ; при
; при 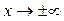 ,
, 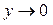 .
.  2) Функция нечетная:
2) Функция нечетная: 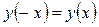 . Построим график для
. Построим график для 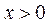 и отобразим его нечетным образом относительно начала координат. 3) Точка пересечения с осью
и отобразим его нечетным образом относительно начала координат. 3) Точка пересечения с осью 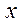 определяется условием
определяется условием 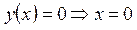 ,
, 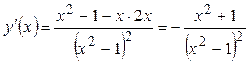 ,
, 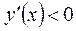 для всех
для всех 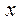 из области определения, т.е. функция является убывающей и не имеет экстремумов.
из области определения, т.е. функция является убывающей и не имеет экстремумов. 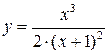 и постройте её график. РЕШЕНИЕ: 1) Функция определена всюду, кроме точки
и постройте её график. РЕШЕНИЕ: 1) Функция определена всюду, кроме точки 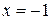 . График функции имеет вертикальную асимптоту
. График функции имеет вертикальную асимптоту 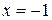 . 2) Точка пересечения с осями:
. 2) Точка пересечения с осями: 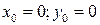 . 3) Выясним, существуют ли наклонные асимптоты. Вычислим пределы:
. 3) Выясним, существуют ли наклонные асимптоты. Вычислим пределы: 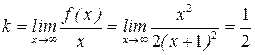 ;
; 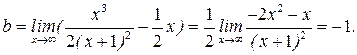
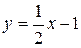 является наклонной асимптотой. 4) Находим производную:
является наклонной асимптотой. 4) Находим производную: 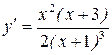 . Знак производной определяется знаком дроби
. Знак производной определяется знаком дроби 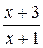 . При
. При 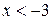 и
и 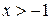
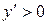 , а при
, а при 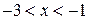
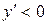 . Интервалы возрастания есть
. Интервалы возрастания есть 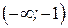 и
и 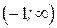 ; интервал убывания
; интервал убывания 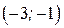 . В области определения функции производная существует всюду и обращается в ноль при
. В области определения функции производная существует всюду и обращается в ноль при 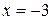 и
и  . При
. При 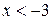
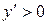 , а при
, а при 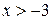
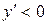 . Следовательно, точка
. Следовательно, точка 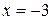 является точкой максимума. Находим значение функции при
является точкой максимума. Находим значение функции при 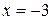 :
: 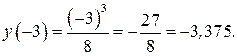 При переходе через другую критическую точку
При переходе через другую критическую точку  производная знак не меняет, т.е.
производная знак не меняет, т.е.  не является точкой экстремума. 5) Находим вторую производную
не является точкой экстремума. 5) Находим вторую производную 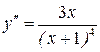 . Видим, что
. Видим, что 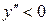 при
при 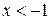 , интервал
, интервал 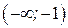 является областью выпуклости.
является областью выпуклости. 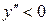 также при
также при 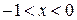 - это тоже область выпуклости;
- это тоже область выпуклости; 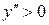 при
при 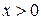 - это область вогнутости. В области определения функции
- это область вогнутости. В области определения функции 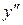 существует всюду;
существует всюду; 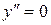 при
при  . Так как при переходе через эту точку
. Так как при переходе через эту точку 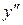 меняет знак, то
меняет знак, то  есть абсцисса точки перегиба. Находим
есть абсцисса точки перегиба. Находим 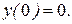
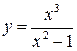 и постройте её график. РЕШЕНИЕ: 1). Функция определена всюду, кроме точек
и постройте её график. РЕШЕНИЕ: 1). Функция определена всюду, кроме точек 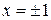 . Точки пересечения графика с координатными осями:
. Точки пересечения графика с координатными осями: 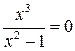
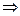
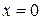
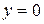 - точка пересечения с осями. 2). Функция нечетная,
- точка пересечения с осями. 2). Функция нечетная, 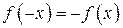 , график симметричен относительно начала координат, достаточно исследовать функцию при
, график симметричен относительно начала координат, достаточно исследовать функцию при 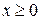 . 3). Точка
. 3). Точка 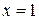 является точкой разрыва II-рода, график функции имеет вертикальную асимптоту
является точкой разрыва II-рода, график функции имеет вертикальную асимптоту 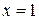 ,
, 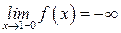 ,
, 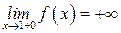 . Выясним, существуют ли наклонные асимптоты. Вычислим пределы:
. Выясним, существуют ли наклонные асимптоты. Вычислим пределы: 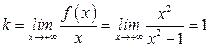 ;
; 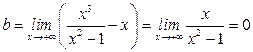 , т.е.,
, т.е., 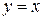 является правой наклонной асимптотой (и левой, так как при операции симметрии прямая переходит сама в себя). 4). Находим производную:
является правой наклонной асимптотой (и левой, так как при операции симметрии прямая переходит сама в себя). 4). Находим производную: 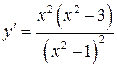 . Знак производной определяется знаком
. Знак производной определяется знаком 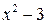 . При
. При 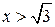
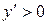 , а при
, а при 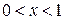 и
и 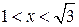
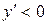 . Интервал возрастания -
. Интервал возрастания - 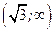 ; интервалы убывания -
; интервалы убывания - 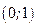 и
и 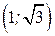 . В области определения функции производная обращается в нуль при
. В области определения функции производная обращается в нуль при  и
и 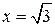 . При
. При 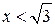
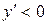 , а при
, а при 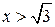
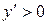 . Следовательно, точка
. Следовательно, точка 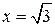 является точкой минимума. Находим значение функции при
является точкой минимума. Находим значение функции при 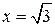 :
: 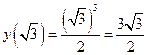 . При переходе через критическую точку
. При переходе через критическую точку  производная знак не меняет, т.е.
производная знак не меняет, т.е.  не является точкой экстремума. 5). Находим вторую производную
не является точкой экстремума. 5). Находим вторую производную 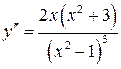 . Видим, что
. Видим, что 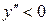 при
при 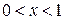 , на интервале
, на интервале 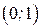 график функции выпуклый вверх. При
график функции выпуклый вверх. При 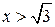
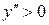 - график функции выпуклый вниз. В области определения функции
- график функции выпуклый вниз. В области определения функции 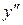 существует всюду;
существует всюду; 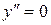 при
при  . Так как при переходе через эту точку
. Так как при переходе через эту точку 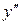 меняет знак, то
меняет знак, то  есть абсцисса точки перегиба. Находим
есть абсцисса точки перегиба. Находим 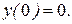
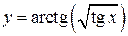 и постройте её график. РЕШЕНИЕ: 1). Так как функция периодична с основным периодом
и постройте её график. РЕШЕНИЕ: 1). Так как функция периодична с основным периодом 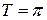 , достаточно исследовать ее поведение на промежутке, длиной равном периоду, например, на
, достаточно исследовать ее поведение на промежутке, длиной равном периоду, например, на 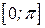 . Арктангенс определен для всех значений аргумента, поэтому областью определения сложной функции
. Арктангенс определен для всех значений аргумента, поэтому областью определения сложной функции 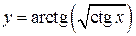 будут промежутки оси
будут промежутки оси 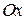 , на которых
, на которых 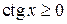 , т.е., для промежутка
, т.е., для промежутка 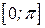 это будет
это будет 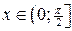 . Для
. Для 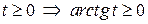 , область значений
, область значений 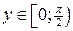 . Точки пересечения графика с координатными осями: при
. Точки пересечения графика с координатными осями: при 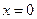 котангенс не определен, точек пересечения с осью
котангенс не определен, точек пересечения с осью 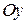 нет. Точки пересечения с осью
нет. Точки пересечения с осью 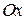 находим, решая уравнение
находим, решая уравнение 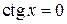
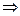
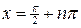 . 2). Четностью или нечетностью функция не обладает. 3). Точка
. 2). Четностью или нечетностью функция не обладает. 3). Точка 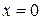 не является точкой разрыва, так как
не является точкой разрыва, так как 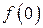 не определена,
не определена, 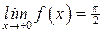 . Поскольку на каждом периоде график
. Поскольку на каждом периоде график 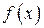 лежит в конечной области плоскости
лежит в конечной области плоскости 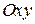 , асимптот у графика существовать не может. 4). Найдем производную:
, асимптот у графика существовать не может. 4). Найдем производную: 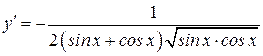 . Для
. Для 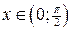
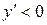 ,
, 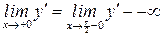 , т.е., на каждом отдельном промежутке области определения функция монотонно убывает. 5).
, т.е., на каждом отдельном промежутке области определения функция монотонно убывает. 5). 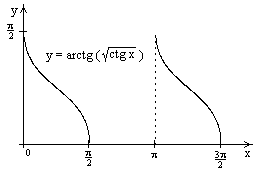 Найдем вторую производную
Найдем вторую производную 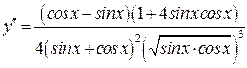 . Корень уравнения
. Корень уравнения 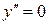 на
на 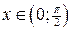 -
- 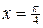 . При
. При 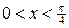
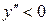 график функции выпуклый вниз, при
график функции выпуклый вниз, при 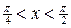
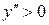 - график функции выпуклый вверх. Точка графика
- график функции выпуклый вверх. Точка графика 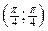 - точка перегиба. График
- точка перегиба. График 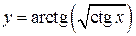 имеет вид
имеет вид 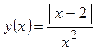 . Область определения функции:
. Область определения функции: 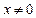 , это точка бесконечного разрыва функции,
, это точка бесконечного разрыва функции, 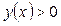 для всех
для всех 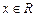 ;
; 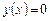 при
при 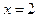 ;
; 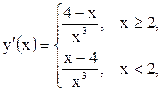
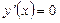 при
при 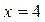 .
.  Построим схему.
Построим схему. 
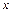
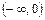
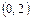
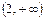
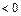
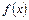



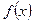 возрастает при
возрастает при 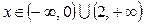 ; убывает при
; убывает при 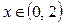 ;
; 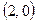 – точка минимума.
– точка минимума.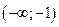
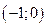
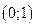
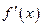
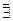

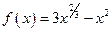 .
.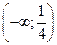
 .
.
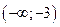
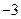
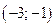
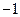

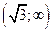
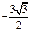
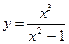 имеет вид:
имеет вид: