Интерполяционный многочлен Лагранжа 4 страница
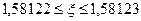
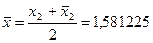
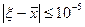
Ответ: 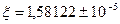
Порядок выполнения работы
Отделить корни уравнения графически и программно. Уточнить корни уравнения методом хорд, методом касательных, комбинированный метод хорд и касательных с точностью 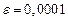 . Нарисовать схему применения метода к каждому корню уравнения.
. Нарисовать схему применения метода к каждому корню уравнения.
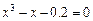 | 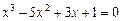 |
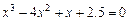 | 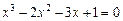 |
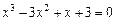 | 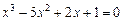 |
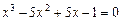 | 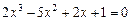 |
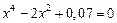 | 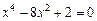 |
Контрольные вопросы
5. В чем заключается этап отделения корней при применении численных методов решения уравнений?
6. Какие свойства функции используются при нахождении промежутков изоляции корня?
7. Какие общие соображения можно использовать для оценки приближенных значений корня?
8. Какие цели преследуются при применении метода половинного деления?
9. Каковы достаточные условия сходимости метода хорд? Какой конец отрезка изоляции корня остается неподвижным в методе хорд?
10. Каковы достаточные условия сходимости метода Ньютона? Как выбирается начальное приближение?
11. В чем смысл комбинированного метода?
12. Какие условия являются критериями достижения заданной точности при решении уравнения методами хорд и Ньютона?
Практическая работа № 10
Тема: «Метод простой итерации»
Основные вопросы: Понятия метода простой итерации. Рекуррентная формула. Итерационная последовательность. Приведение уравнений к виду, пригодному для метода простой итерации. Оценка погрешности приближений.
Краткие теоретические сведения:.
Пусть E= (E,r) - полное метрическое пространство и j(x) – отображение, определенное на E. Если это отображение удовлетворяет двум условиям:
1) j(x)ÎE для любого xÎE, (j – отображение E в себя);
2) Существует 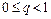 такое, что r (j(x), j(z)) £ q×r(x, z) при "x, zÎE, (j – сжимающее отображение),
такое, что r (j(x), j(z)) £ q×r(x, z) при "x, zÎE, (j – сжимающее отображение),
то существует единственное xÎE такое, что справедливо равенство
x = j (x ) (1)
Точка x называется неподвижной точкой отображения j. Для приближенного вычисления неподвижной точки применяется метод простой итерации, состоящий в построении последовательности {x(n)} по итерационной формуле
x(n+1) = j (x(n) ), n = 0,1,2,…, (2)
начиная из любого начального приближения x(0) Î E.
Условия 1) и 2) являются также и достаточными условиями сходимости метода простой итерации к неподвижной точке x.
Приведенные общие результаты применим к двум частным случаям.
Приложение I.Рассмотрим метрическое пространство
E= ([a; b], | × | ) и функцию j(x), определенную на [a; b]. Неподвижную точку x функции j в силу равенства (1) называют корнем уравнения
x = j (x) (3)
Метод простой итерации (2) для приближенного вычисления корней уравнения (3) запишем в виде:
xn+1 = j (xn ), n = 0,1,2,…. (4)
Условия 1) и 2) существования и единственности корня уравнения (3) и сходимости к нему метода простой итерации (4) удобно записать в виде:
1) j (x) Î[a; b], " x Î[a; b];
2) $ 0 £ q < 1, что | j' (x)| £ q, " x Î[a; b].
«Правило останова»: вычисления прекращаются, когда впервые удовлетворяется неравенство 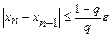 .
.
Искомый приближенный корень 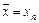 .
.
Примеры решения задач
Вычислить корень 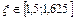 уравнения
уравнения 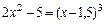 (1) с точностью
(1) с точностью 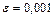 , используя метод простой итерации.
, используя метод простой итерации.
Решение: Уравнение (1) запишем в эквивалентной форме 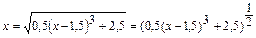 (2) и обозначим
(2) и обозначим 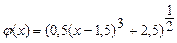 .
.
Проверим выполнение достаточных условий сходимости метода простой итерации. Функция 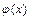 на отрезке
на отрезке 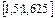 определена и имеет непрерывную производную
определена и имеет непрерывную производную 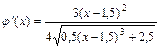 (3)
(3)
Причем 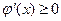 . Поэтому:
. Поэтому:
1. Функция 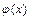 возрастающая, и значит
возрастающая, и значит 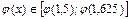 , но
, но 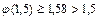 ,
, 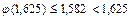 , следовательно,
, следовательно, 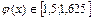
2. Из (3) видно, что с увеличением x числитель возрастает, а значит 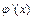 возрастает. Следовательно,
возрастает. Следовательно, 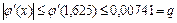
Все условия выполнены. Для достижения заданной точности вычисления следует проводить до момента выполнения неравенства 
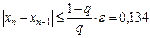 (4)
(4)
Вычисления проводим по формулам 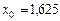 ,
, 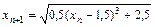
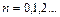
Составим таблицу
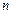 | 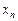 | 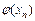 | 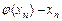 |
| 1,625 | 1,58145 | -0,04355 | |
| 1,58145 | 1,58122 | -0,00023 | |
| 1,58122 | 1,58122 | 0,0000035 | |
В силу (4) вычисления прекращаются 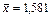
Ответ: 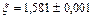
Порядок выполнения работы
Уточнить один из корней уравнения методом итерации с точностью 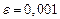 , указать число итераций. Нарисовать схему применения метода итерации к данному корню уравнения.
, указать число итераций. Нарисовать схему применения метода итерации к данному корню уравнения.
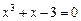 | 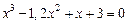 |
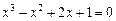 | 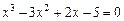 |
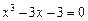 | 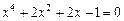 |
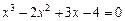 | 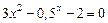 |
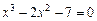 | 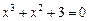 |
Контрольные вопросы
1) Как отделяются корни уравнения?
2) Какой должна быть величина шага при отделении корней?
3) Какие условия должны быть выполнены для применения метода итерации?
4) Какова идея метода итерации? Геометрическая иллюстрация.
5) Какое условие должно выполняться для сходимости итерационной последовательности?
6) Как находится равносильное уравнение, применяемое для итерационного процесса? Критерий выбора равносильного уравнения.
7) Как определяется погрешность метода итерации при заданной точности?
8) Какие положительные и отрицательные стороны метода итерации (сравнить с методом деления отрезка пополам)?
Практическая работа № 11
Тема: «Интерполирование табличных функций. Многочлен Лагранжа»
Основные вопросы: Понятие табличной функции. Задача аналитического приближения табличных функций. Постановка задачи об апроксимации функций. Интерполяция. Оценка погрешности интерполяции. Интерполяционный многочлен в форме Лагранжа.
Краткие теоретические сведения:
Постановка задачи: пусть задана табличная функция в n+1 точках x0, x1, x2,…, xn известны значения функции y=f(x): f(x0)=y0, f(x1)=y1, f(x2)=y2,…, f(xn)=yn.
| …. | n | ||||
| xi | x0 | x1 | x2 | …. | xn |
| yi | y0 | y1 | y2 | … | yn |
Требуется подобрать достаточно простую функцию F(x), удовлетворяющую условиям: в точках x0, x1, x2,…, xn значения функции F(x) должны совпадать со значениями данной функции f(x), то есть F(xk)= f(xk), k=0, 1, 2, …, n.
При остальных значениях x из области определения будем считать, что выполняется приближенное равенство f(x)» F(x).
Функция F(x) называется интерполирующей, процесс ее построения – интерполированием, а точки x0, x1, x2,…, xn – узлами интерполяции. Часто в качестве функции F(x) берется многочлен Pn(x), который называется интерполяционным многочленом.
Интерполяционный многочлен Лагранжа
Многочлен вида
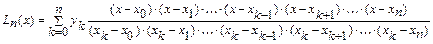
называется интерполяционным многочленом Лагранжа. Многочлен Лагранжа можно построить для любой таблично заданной функции. Оценка погрешности: 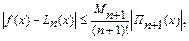
где 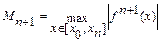 ,
, 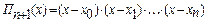 .
.
На практике такая оценка погрешности, как правило, оказывается завышенной.
Примеры решения задач
1. По таблице значений функции
2.
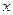 | -8 | -5 | |
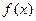 | -2 |
Составить интерполяционный многочлен Лагранжа. Построить его график и отметить на нем точки 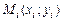 ,
, 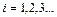
Решение: Запишем формулу Лагранжа для случая n=2 и подставим значение из нашей таблицы
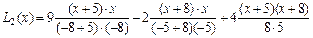
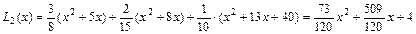
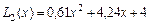
Построим график функции 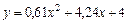 .
.
 |
Рисунок 19
Выделив полный квадрат, получаем 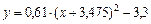 .
.
3. По заданной таблице значений функции
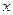 | 1,2 | 1,9 | 3,3 | 4,7 | 5,4 | 6,8 | 7,5 |
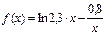 | 0,3486 | 1,0537 | 1,7844 | 2,2103 | 2,3712 | 2,6322 | 2,7411 |
Вычислить значение этой функции в одном промежуточном значении xс помощью интерполяционного многочлена Лагранжа. Оценить погрешность интерполяции.
Решение: 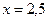 . По количеству узловыхточек требуется вычислить значение
. По количеству узловыхточек требуется вычислить значение 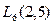
Вычисления проводятся по таблице:
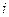 | ||||||
| 1,3 | -0,7 | -2,1 | -3,5 | -4,2 | -5,6 | |
| 0,7 | 0,6 | -1,4 | -2,8 | -3,5 | -4,9 | |
| 2,1 | 1,4 | -0,8 | -1,4 | -2,1 | -3,5 | |
| 3,5 | 2,8 | 1,4 | -2,2 | -0,7 | -2,1 | |
| 4,2 | 3,5 | 2,1 | 0,7 | -2,9 | -1,4 | |
| 5,6 | 4,9 | 3,5 | 2,1 | 1,4 | -4,3 | |
| 6,3 | 5,6 | 4,2 | 2,8 | 2,1 | 0,7 |
Вычислим 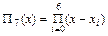
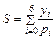
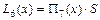
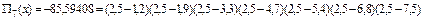
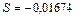
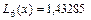
Для оценки погрешности интерполяционной формулы в точке xнадо найти 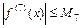
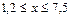
Тогда 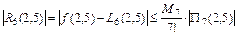
Вычислим 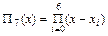
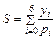
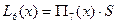
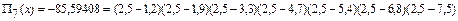
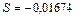
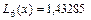
Для оценки погрешности интерполяционной формулы в точке xнадо найти 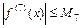 ,
, 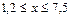
Тогда 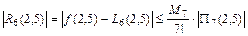 функция
функция 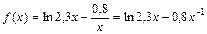
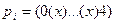 | 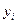 | 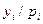 | |
| -6,3 | 991,075 | 0,3486 | 0,00035 |
| -5,6 | -158,120256 | 1,0537 | -0,00666 |
| -4,2 | -101,64874 | 1,7844 | -0,01755 |
| -2,8 | 124,23734 | 2,2103 | 0,01779 |
| -2,1 | -184,23833 | 2,3712 | -0,01287 |
| -0,7 | 849,89638 | 2,6322 | 0,00309 |
| -5 | -3049,6208 | 2,7411 | -0,00089 |
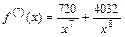 и
и 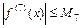
Следовательно 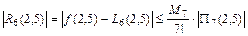
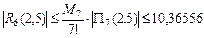
Ответ: 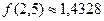
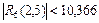
функция 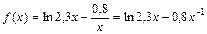
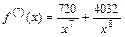 и
и 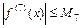
Следовательно 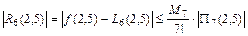
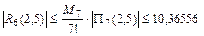
Ответ: 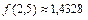 ,
, 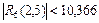
Порядок выполнения работы
1. По заданной таблице значений функции
| х | xi | x0 | x1 | x2 | … | xn |
| f(x) | yi | y0 | y1 | y2 | … | yn |
составить интерполяционный многочлен Лагранжа и построить его график.
| x0 | x1 | x2 | x3 | y0 | y1 | y2 | y3 | |
| -1 | -3 | |||||||
| -1 | -4 | |||||||
| -4 | -2 | |||||||
| -3 | -1 | -1 | ||||||
| -1 | -5 | -3 | -7 | |||||
| -2 | -1 | |||||||
| -3 | ||||||||
| -4 | -2 | |||||||
| -3 | -1 | 1,5 | -7 |
2. По заданной таблице значений функции вычислить значение этой функции в одном промежуточном значении x с помощью интерполяционного многочлена Лагранжа. Найти значение функции в точке x из ее аналитического выражения и вычислить абсолютную погрешность интерполяции.
| x | 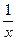 lgx+x2 lgx+x2 | |
| 1,3 | 1,7777 | |
| 2,1 | 4,5634 | |
| 3,7 | 13,8436 | |
| 4,5 | 20,3952 | |
| 6,1 | 37,3387 | |
| 7,7 | 59,4051 | |
| 8,5 | 72,3593 | |
| 8,8 | 77,5473 | |
| 9,3 | 86,5941 | |
| 10,4 | 108,2578 |
| x | 3,8 | 9,1 | 2,9 | 4,4 | 10,0 | 5,8 | 8,6 | 4,1 | 1,5 |
Контрольные вопросы
1. Как ставится задача интерполирования функции?
2. Как обосновывается существование и единственность интерполяционного многочлена? Как связана его степень с количеством узлов интерполяции?
3. Как строятся интерполяционный многочлен Лагранжа? В чем особенность этого способа интерполяции?
4. Какова оценка погрешности интерполяционных формул, если интерполируемая функция задана аналитически? Как изменяется эта оценка, когда функция задана таблично?
Практическая работа № 12
Тема: «Интерполирование табличных функций. многочлен Ньютона»
Основные вопросы: Понятие конечной разности первого, второго, n-го порядка. Первый интерполяционный многочлен Ньютона. Второй интерполяционный многочлен Ньютона. Оценка погрешности.
Краткие теоретические сведения:
Пусть функция y=f(x) задана таблицей с постоянным шагом h:
| xi | x0 | x1 | x2 | … | xn |
| yi | y0 | y1 | y2 | … | yn |
где xi=x0+ih, i=1,2,…,n. Такую таблицу называют таблицей с равноотстоящими узлами. Для таблицы с равноотстоящими узлами определяются конечные разности. Конечными разностями первого порядка называются числа, равные приращениям значений функции
Dy0=y1-y0, Dy1=y2-y1, …, Dyn-1=yn-yn-1.
Конечными разностями порядка k, k³2 называются числа, определенные равенствами: Dkym=Dk-1ym+1 -Dk-1ym.
Положим 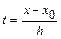 , тогда
, тогда 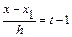 ,
, 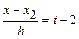 , …,
, …, 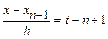 . Многочлен вида
. Многочлен вида
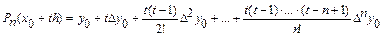
называется первым интерполяционным многочленом Ньютона. Его удобно использовать для нахождения значения таблично заданной функции в промежуточной точке, расположенной ближе к началу таблицы, причем в качестве точки x0 следует брать ближайший к ней слева узел интерполяции 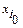 и положить
и положить 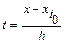 . Первый многочлен Ньютона в этом случае примет вид
. Первый многочлен Ньютона в этом случае примет вид
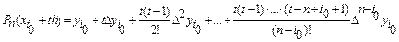 .
.
Если требуется найти значение таблично заданной функции в точке, расположенной ближе к концу таблицы, то используется второй интерполяционный многочлен Ньютона, который определяется формулой
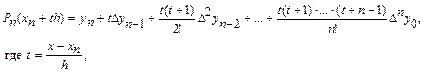 причем в качестве xn следует брать ближайший к точке x справа узел интерполяции
причем в качестве xn следует брать ближайший к точке x справа узел интерполяции 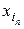 .
.
Примеры решения задач
