Приведение уравнения второго порядка к каноническому виду. Окружность. Центр окружности

ВОПРОС№23 Окружность

Окружность. Центр окружности. Радиус окружности.

Уравнение окружности. Уравнение касательной к окружности.

Условие касания прямой и окружности.

Окружностью ( рис.1 ) называется геометрическое место точек, равноудалённых от данной точки О, называемой центром окружности, на расстояние R . Число R > 0 называется радиусом окружности.

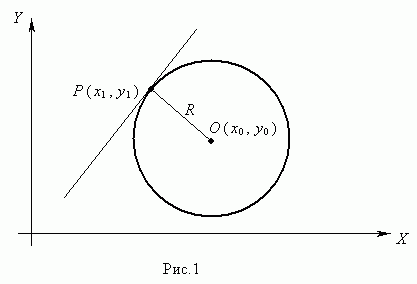
Уравнение окружности радиуса R с центром в точке О ( х₀ , у ₀ ) имеет вид:

( х – х₀ ) ² + ( у – у ₀ ) ² = R ² .

Если центр окружности совпадает с началом координат, то уравнение окружности упрощается:

х ² + у ² = R ² .

Пусть Р ( х₁ , у ₁ ) – точка окружности ( рис.1 ), тогда уравнение касательной к окружности в данной точке имеет вид:

( х₁ – х₀ ) ( х – х₀ ) + ( у₁ – у ₀ ) ( у – у ₀ ) = R ² .

Условие касания прямой y = m x + k и окружности х ² + у ² = R ² :

k 2 / ( 1 + m ² )= R ² .

ВОПРОС№24,25,26

Эллипс.

Определение 11.2. Эллипсомназывается множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F₁ и F₂ этой плоскости, называемых фокусами, есть величина постоянная.

Замечание. При совпадении точек F₁ и F₂ эллипс превращается в окружность.

Выведем уравнение эллипса, выбрав декартову систему

у М(х,у) координат так, чтобы ось Ох совпала с прямой F₁F₂, начало

r₁ r₂ координат – с серединой отрезка F₁F₂. Пусть длина этого

отрезка равна 2с, тогда в выбранной системе координат

F₁ O F₂ x F₁(-c, 0), F₂(c, 0). Пусть точка М(х, у) лежит на эллипсе, и

сумма расстояний от нее до F₁ и F₂ равна 2а.

Тогда r₁ + r₂ = 2a, но ,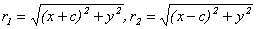

поэтому 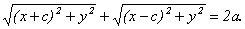Введя обозначение b² = a²-c² и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса: 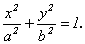(11.1)

Определение 11.3. Эксцентриситетом эллипса называется величина е=с/а (11.2)

Определение 11.4. Директрисой D_i эллипса, отвечающей фокусу F_i, называется прямая, расположенная в одной полуплоскости с F_i относительно оси Оу перпендикулярно оси Ох на расстоянии а/е от начала координат.

Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением (11.1), а уравнением второй степени другого вида.

Свойства эллипса:

1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2а и 2b (2a>2b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью.

2) Весь эллипс содержится внутри прямоугольника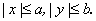

3) Эксцентриситет эллипса e < 1.

Действительно,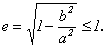

4) Директрисы эллипса расположены вне эллипса (так как расстояние от центра эллипса до директрисы равно а/е, а е<1, следовательно, а/е>a, а весь эллипс лежит в прямоугольнике )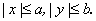

5) Отношение расстояния r_i от точки эллипса до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса.

Доказательство.

Расстояния от точки М(х, у) до фокусов эллипса можно представить так:

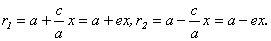Составим уравнения директрис:

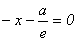(D₁), 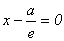(D₂). Тогда 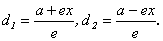Отсюда r_i / d_i = e, что и требовалось доказать.

Гипербола.

Определение 11.5. Гиперболойназывается множество точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F₁ и F₂ этой плоскости, называемых фокусами, есть величина постоянная.

Выведем каноническое уравнение гиперболы по аналогии с выводом уравнения эллипса, пользуясь теми же обозначениями.

|r₁ - r₂| = 2a, откуда 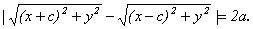Если обозначить b² = c² - a², отсюда можно получить

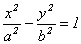- каноническое уравнение гиперболы. (11.3)

Определение 11.6. Эксцентриситетом гиперболы называется величина е = с / а.

Определение 11.7. Директрисой D_i гиперболы, отвечающей фокусу F_i, называется прямая, расположенная в одной полуплоскости с F_i относительно оси Оу перпендикулярно оси Ох на расстоянии а / е от начала координат.

Свойства гиперболы:

1) Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.

2) Ветви гиперболы имеют две асимптоты, определяемые уравнениям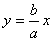и

и .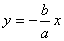

3) Наряду с гиперболой (11.3) можно рассмотреть так называемую сопряженную гиперболу, определяемую каноническим уравнением

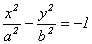, (11.3`)

для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот.

4) Эксцентриситет гиперболы e > 1.

5) Отношение расстояния r_i от точки гиперболы до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.

Доказательство можно провести так же, как и для эллипса.

Парабола.

Определение 11.8. Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фокусом параболы, а прямая – ее директрисой.

у Для вывода уравнения параболы выберем декартову

систему координат так, чтобы ее началом была середина

d M(x,y) перпендикуляра FD, опущенного из фокуса на директри-

r су, а координатные оси располагались параллельно и

перпендикулярно директрисе. Пусть длина отрезка FD

D O F x равна р. Тогда из равенства r = d следует, что

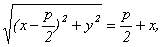поскольку

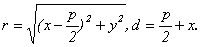Алгебраическими преобразованиями это уравнение можно привести к виду: y² = 2px , (11.4)

называемому каноническим уравнением параболы. Величина р называется параметромпараболы.

Свойства параболы:

1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной – начало координат.

2) Вся парабола расположена в правой полуплоскости плоскости Оху.

Замечание. Используя свойства директрис эллипса и гиперболы и определение параболы, можно доказать следующее утверждение:

Множество точек плоскости, для которых отношение е расстояния до некоторой фиксированной точки к расстоянию до некоторой прямой есть величина постоянная, представляет собой эллипс (при e<1), гиперболу (при e>1) или параболу (при е=1).

Приведение уравнения второго порядка к каноническому виду.

Определение 11.9. Линия, определяемая общим уравнением второго порядка

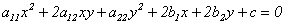, (11.5)

называется алгебраической линией второго порядка.