Приведение уравнения второго порядка к каноническому виду

Определение 11.9. Линия, определяемая общим уравнением второго порядка

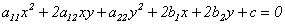, (11.5)

называется алгебраической линией второго порядка.

Для квадратичной формы 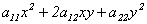можно задать матрицу

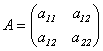. (11.6)

Для того, чтобы перейти к новой системе координат, в которой уравнение линии будет иметь канонический вид, необходимо провести два преобразования:

1) поворот координатных осей на такой угол, чтобы их направление совпало с направлением осей симметрии кривой (если она имеет две оси);

2) параллельный перенос, при котором начало координат совмещается с центром симметрии кривой (если он существует).

Замечание. Для параболы новые оси координат должны располагаться параллельно и перпендикулярно директрисе, а начало координат – совпасть с вершиной параболы.

Поскольку в канонических уравнениях кривых второго порядка отсутствуют произведения переменных, необходимо перейти к координатной системе, определяемой базисом из ортонормированных собственных векторов матрицы А. В этом базисе уравнение (11.5) примет вид:

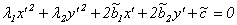(в предположении, что λ_1,2 не равны 0).

Зададим последующий параллельный перенос формулами:

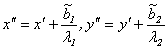. Получим в новой координатной системе уравнение

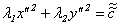. (11.7)

Рассмотрим возможные геометрические образы, определяемые этим уравнением в зависимости от знаков λ₁, λ₂ и :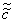

1) если собственные числа матрицы А λ₁ и λ₂ и 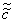одного знака, уравнение (11.7) представляет собой каноническое уравнение эллипса:

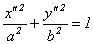, где

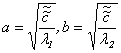
(случа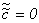и и 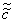, имеющего знак, противоположный знаку λ₁, λ₂, будут рассмотрены в следующей лекции).

2) если λ₁ и λ₂ имеют разные знаки, уравнение (11.7) является каноническим уравнением гиперболы:

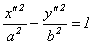или 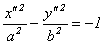, в зависимости от знака .

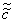В случае, когда одно из собственных чисел матрицы А равно 0, уравнение (11.5) в результате двух преобразований координат можно привести к виду:

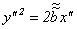, (11.8)

являющимся каноническим уравнением параболы.

Пример.

Приведем к каноническому виду уравнение второго порядка

3x² + 10xy +3y² - 2x – 14y – 13 = 0.

Матрица квадратичной формы 3x² + 10xy + 3y² имеет вид:

.

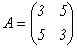Найдем ее собственные числа и собственные векторы. Составим характеристическое уравнение: 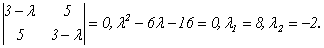Для координат собственного вектора е₁, соответствующегоλ₁, получим с учетом нормировки:

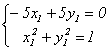, откуда e₁ = { 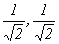}. Аналогично найдем е₂: ,

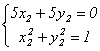e₂ = { 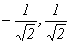}. Составим матрицу перехода к новому базису, столбцами которой будут координаты собственных векторов: 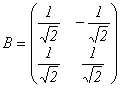. Тогда

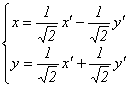. Подставив эти выражения в исходное уравнение, получим его вид в новой системе координат: 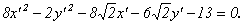Заметим, что коэффициентами при x² и y² являются λ₁ и λ₂.

Преобразуем полученное уравнение: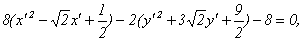

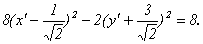Зададим параллельный перенос формулами: 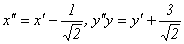. Получим уравнение: 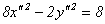, а после деления на 8:

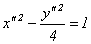- каноническое уравнение гиперболы.

Лекция 12.

Классификация кривых второго порядка на плоскости. Поверхности второго порядка. Канонические уравнения основных поверхностей второго порядка: эллипсоидов, гиперболоидов и параболоидов.