ЗАДАЧА №1
Студент 4 курса Преподаватель
Мыльников Е.А.
Шифр: 0813 - п/АТС-1034
МОСКВА 2012 г.
ЗАДАЧА №1
На испытание поставлено No изделий. За время t ч вышло из строя п(t) штук изделий. За последующий интервал времени Dt вышло из строя п(Dt) изделий. Необходимо вычислить вероятность безотказной работы за время t и t+Dt,частоту отказов и интенсивность отказов на интервале Dt. Исходные данные для решения задачи приведены в таблице 1.
Таблица 1.
| Предпоследняя цифра шифра | Последняя цифра шифра | No | t,ч | Dt | п(t) | п(Dt) |
| нечетная |
Решение:
1. Построим временной график.
 |
t
 |
= 0 t = 1300 ч Dt = 100 ч
No = 1000 п(t) = 288 п(Dt) = 13 t
Ni = 712 Ni+ 1= 699
2. Определим вероятность безотказной работы.
Вероятность безотказной работыили функция надежности P(t) выражает вероятность того, что невосстанавливаемый объект не откажет к моменту времени наработки t.
Определим вероятность безотказной работы для tн = 1300ч.(начало интервала) по формуле:

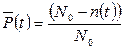
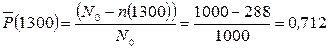
Определим вероятность безотказной работы для tк = 1300 + 100 = 1400 ч. (конец интервала).
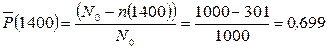
Определим среднее число исправно работающих образцов в интервале Dt
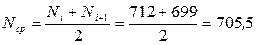
Число отказавших изделий за время t = 1350 ч:
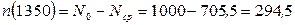 ,
,
тогда 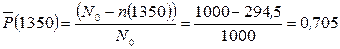
3. Определим частоту отказов на интервале Dt.
Частотой отказов называют плотность распределения наработки до отказа. Экспериментально частота отказов определяется как отношение числа отказавших объектов в единицу времени к первоначальному числу объектов при условии, что все вышедшие из строя объекты не восстанавливаются. Частоту отказов можно определить по формуле:
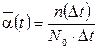
где п(Dt) - число отказавших объектов в интервале времени от t - Dt /2 до t + Dt /2.
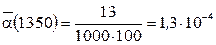 1/ч
1/ч
4. Определяем интенсивность отказов на интервале Dt.
Интенсивность отказов l(t) выражает интенсивность процессов возникновения отказов. Статистическая интенсивность отказов определяется отношением числа отказавших объектов в единицу времени к среднему числу объектов, исправно работающих в данный отрезок времени.
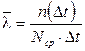 ,
,
где Nср - среднее число исправно работающих объектов в интервале Dt;
Ni - число объектов, исправно работающих в начале интервала Dt;
Ni+1 - число объектов, исправно работающих в конце интервала Dt.
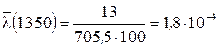 1/ч
1/ч
Вероятностная оценка этой характеристики находится из выражения:
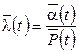
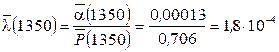 1/ч
1/ч
