Методические указания к задаче 6

Решение задачи необходимо начать с проработки материала в [2- с.13-16, 295-298, 300-301; 8- с.6-13]. Обратите внимание на примеры 17.2 [2] и 1.1, 1.3 [8].

Следует различать единицы измерения количества информации «бит», скорости передачи информации (информационной скорости передачи) «бит/с» и скорости модуляции (технической скорости передачи) «Бод».

Учитывая, что элементы «1» и «0» двоичного кода составляют полную группу событий, вероятность появления элемента «0» на позициях кодовой комбинации равна:

р_i (0) = 1 - р_i (1) (6.1)

Количество информации, содержащееся в единичных элементах «1» и «0» на позициях кода равны:

I_i (1) = log₂[1/ р_i (1)] = - log₂ р_i (1), бит; (6.2)

I_i (0) = log₂[1/ р_i (0)] = - log₂ р_i (0), бит. (6.3)

Для вычисления двоичных логарифмов можно воспользоваться формулами перехода в логарифмах к другому основанию:

log₂ z = ln z / ln 2 ≈ 1,443∙ln z = lg z / lg 2 ≈ 3,32∙lg z. (6.4)

Энтропия двоичного элемента рассчитывается по формуле:

Н_эл.i = р_i (1)∙I_i (1) + р_i (0)∙I_i (0), бит/эл. (6.5)

Для расчета энтропии знака (кодовой комбинации) необходимо определить длину кодовой комбинации k равномерного двоичного кода для кодирования К

знаков источника :

k = 1 + ЦЧ[log₂ К], элементов, при дробном значении log₂ К (6.6 а)

k = log₂ К, элементов, при целом значении log₂ К (6.6 б)

где: ЦЧ[ ] – целая часть полученного значения.

Энтропия знака, закодированного k элементной кодовой комбинацией:

Н_зн. = Н_к.к. = 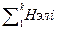= Н_эл.1 + Н_эл.2 + ... + Н_эл.k , бит/знак (6.7)

Максимальное возможное значение энтропии достигается при равной вероятности появления элементов, т. е. при р_i (1) = р_i (0) = 0,5. Тогда она равна :

Н_{эл.i макс.} = (- 0,5 ∙ log₂ 0,5) + (- 0,5 ∙ log₂ 0,5) = log₂ 2 = 1 бит/эл.

Максимальная энтропия знака при этом будет равна: Н_{зн.макс.}= k, бит/знак.

Избыточность источника дискретных сообщений оценивается долей от максимально возможного значения энтропии, неиспользуемой источником. Коэффициент избыточности источника равен:

ǽ = (Н_{зн.макс.} - Н_зн.) / Н_{зн.макс.} = 1 – Н_зн. / Н_{зн. макс.} (6.8)

Зная скорость передачи по каналу N знак/мин., длину кодовой комбинации знака, можно определить скорость модуляции – количество единичных элементов передаваемых в единицу времени (в секунду). Скорость передачи информации определяется с учетом среднего количества информации (энтропии) в одном знаке и количества знаков, передаваемых в секунду (N/60).

С кодированием знаков двоичным кодом можно ознакомиться в [8- с.8-11].

Пример кодирования двоичным кодом десятичного числа (знака) «19» для k = 7 приведен в таблице 8.

Таблица 8

Разряды кодовой комбинации	х	х	х	х	х	х	х
Веса разрядов	26 = 64	25=32	24 =16	23 =8	22 =4	21 =2	20 =1

Число 19 можно представить суммой весов разрядов двоичного кода:

19 = 16 + 2 + 1. Тогда на месте разрядов (х), которые участвовали в сумме ставится элемент «1», а на месте разрядов не участвовавших в сумме – элемент «0». Кодовая комбинация будет иметь вид 0010011

Количество информации в кодовой комбинации знака определяется суммой количества информации в элементах кодовой комбинации с учетом того, какой элемент стоит на каждой позиции (разряде) кодовой комбинации своего знака:

I_к.к. = I_зн = I₁(1) или I₁(0) + I₂(1) или I₂(0) + ... + I_k(1) или I_k(0), бит (6.9)

Например, для кодовой комбинации числа 19:

I_{к.к. 19} = I₁(0)+ I₂(0)+ I₃(1)+ I₄(0)+ I₅(0)+ I₆(1)+ I₇(1), бит.

Задача 7

Задана 4-х разрядная кодовая комбинация простого первичного кода Q(0,1)

(таблица 10).

Требуется:

1. Закодировать ее помехоустойчивым циклическим кодом, исправляющим однократную ошибку (t_испр. = 1).

2. Проверить правильность построения кодовой комбинации циклического кода F(0,1).

3. Составить таблицу синдромов циклического кода.

4. Проверить, будет ли исправлена однократная ошибка в i-м разряде

(таблица 10) кодовой комбинации циклического кода.

5. Построить структурную схему кодера циклического кода.

Для вариантов 00, 04, 40 и 44, для которых по таблице 9 выходит нулевая

кодовая комбинация (0000), следует взять кодовую комбинацию (только ее) по

вариантам 01, 05, 41 и 45, а номер ошибочного разряда i – по своему варианту.

Таблица 9

Последняя цифра номера варианта
Первая половина кодовой комбинации
Номер ошибочного разряда i
Предпоследняя цифра номера варианта
Вторая половина кодовой комбинации

Методические указания к задаче 7.

Для решения задачи необходимо проработать материал в [2- с.310-311, 315-318; 8- с.102-104, 110-118, 127-129], обратив особое внимание на примеры 18.1, 18.2, 18.5, 18.6 [2], а особенно 6.3 – 6.6 [8].

При определении минимального кодового расстояния d₀ кода, который может исправить t_испр. ошибок воспользуйтесь выражением (18.4) [2], или (6.6) [8]. Следует помнить, что только для кода с d₀ = 3 известно точное соотношение для определения количества проверочных элементов r: (6.9) [8], где n = k+r. Здесь k- длина кодовой комбинации простого кода (количество информационных элементов), n- общая длина корректирующего кода. Это соотношение можно также представить в виде:

2^r ≥ r+k+1 (7.1)

Согласно соотношению (7.1), подбором, определяется значение r, удовлетворяющее ему.

Образующий полином следует выбрать из таблицы 18.1 [2- с.316], или таблицы 6.2 [8- с.114], степень его равна r.

Пункт 1 задания следует выполнять в следующей последовательности: определить d₀, затем r и n, выбрать образующий полином и составить кодовую комбинацию циклического кода. Кодирование циклическим кодом может быть проведено как в алгебраическом, так и в цифровом виде. Кодирование циклическим кодом рассмотрено в примерах 18.5 [2], 6.3 [8].

Правильность построения кодовой комбинации проверяется делением составленной комбинации на образующий полином. Если при делении получится ненулевой остаток, это говорит о неверном кодировании, т. е. полученная кодовая комбинация относится к запрещенным комбинациям этого кода. Получение нулевого остатка (деление без остатка) говорит о верном

кодировании, то есть. кодовая комбинация является разрешенной.

При составлении таблицы синдромов используйте материал [2- с.317-318]. В таблице 18.2 [2] приведен пример таблицы синдромов.

Проверка возможности исправления ошибки заключается во введении ошибки в заданный разряд кодовой комбинации, делении ее на образующий полином, нахождении остатка и в определении соответствия полученного остатка

(синдрома) синдрому кода при ошибке в этом разряде.

Схему кодера выполнять по типу рис. 6.9 в [8]. Следует иметь в виду, что число ячеек сдвигающего регистра и регистра задержек выбирается равным степени образующего полинома, а число сумматоров – на единицу меньше веса образующего полинома. Сумматоры по модулю два включаются перед ячейками, которые стоят на позициях единиц в образующем полиноме, за исключением старшего разряда. Например, если образующий полином Р(х)=х³+х²+1, что соответствует Р(0,1) = 1101, тогда регистр сдвига должен иметь 3 ячейки (образующий полином 3-ей степени), в него включаются два сумматора (так как вес образующего полинома W=3), сумматоры включаются перед первой и третьей ячейками.

ПРИЛОЖЕНИЕ

1. Тригонометрические формулы преобразования.

cosX∙cosY = 1/2∙cos(X+Y) + 1/2∙cos(X-Y);

cos(Х+Y) = cosХ∙cosY - sinX∙sinY; cos(Х-Y) = cosХ∙cosY + sinX∙sinY;

1 – cosX = 2∙sin²(Х/2); 1 + cosX = 2∙cos²(Х/2);

cosX + cosY = 2∙cos[(X+Y)/2]∙cos[(X-Y)/2];

cosX - cosY = -2∙sin[(X+Y)/2]∙sin[(X-Y)/2];

sinX + sinY = 2∙sin[(X+Y)/2]∙cos[(X-Y)/2];

sinX - sinY = 2∙sin[(X-Y)/2]∙cos[(X+Y)/2].

2. Формулы расчета коэффициентов Берга.

γ₀(θ) = 1/π ∙ (sin θ - θ∙cos θ); γ₁(θ) = 1/π ∙ (θ - sin θ ∙cos θ); γ_n(θ) = I_n/SU;

γ_n(θ) = [2/π ∙ (sin nθ∙cos θ - n∙cos nθ∙sin θ)] / [n ∙ (n² – 1)], n = 2, 3, ... ;

3. Формулы расчета различных интегралов.

∫exp(-ax²)∙cos(bx)∙dx = √π/4a∙exp(-b²/4a);

∫[cos(ax) / (b²+x²]∙dx = π/2b∙exp(-b∙a); ∫[1/ (b²+x²]∙dx = 1/b∙arctg(х/b);

∫ exp(-аx²)∙dx = 1/2∙√π/а; ∫[х∙sin(ax) / (1+x²)]∙dx = π/2∙exp(-a);

∫ [x² ∙ cos(ax) / (1+x²)] ∙dx = π∙δ(a) - π/2∙exp(-a);

Формула интегрирования по частям: ∫u∙dv = u∙v - ∫v∙du;

Пример: ∫х∙cos(ax)∙dx = 1/а∙х∙sin(ax) + 1/а² ∙cos(ax).

4. Расчет значений интеграла вероятностей.

Интеграл вероятностей Ф(х) = 1 / √2π ∙ ∫exp(-t²/2)∙dt;

Используются также другие виды интеграла вероятностей:

Ф₀(х) = 1 / √2π ∙ ∫exp(-t²/2)∙dt;

Ф'(х) = 2 / √2π ∙ ∫exp(-t²/2)∙dt (функция Крампа).

Взаимосвязь между различного вида интегралами вероятности:

Ф(х) = 0,5 + Ф₀(х) = 0,5[1 + Ф'(х)].

Значения интегралов вероятности в характерных точках:

Ф(-х) = 1 - Ф(х); Ф₀(-х) = - Ф₀(х); Ф'(-х) = - Ф'(х);

Ф(-∞) = 0; Ф(0) = 0,5; Ф₀(-∞) = 0; Ф₀(0) = 0; Ф'(-∞) = 0; Ф' (0) = 0;

Ф(∞) = 1; Ф₀(∞) = 0,5; Ф'(∞) = 1.

Значения интеграла вероятностей Ф(х) приведены в таблице П.1

Таблица П.1

х	Ф(х)	х	Ф(х)	х	Ф(х)	х	Ф(х)
0,1	0,54	1,1	0,864	2,1	0,982	3,1	0,999
0,2	0,579	1,2	0,885	2,2	0,986	3,2	0,9993
0,3	0,618	1,3	0,903	2,3	0,989	3,3	0,9995
0,4	0,655	1,4	0,919	2,4	0,992	3,4	0,9997
0,5	0,691	1,5	0,933	2,5	0,994	3,5	0,99976
0,6	0,726	1,6	0,945	2,6	0,995	3,6	0,99984
0,7	0,758	1,7	0,955	2,7	0,996	3,7	0,99989
0,8	0,788	1,8	0,964	2,8	0,997	3,8	0,99992
0,9	0,816	1,9	0,971	2,9	0,998	3,9	0,99995
1,0	0,841	2,0	0,977	3,0	0,9987	4,0	0,99997

Более подробную таблицу значений интеграла вероятностей можно найти

в [13]. Значения его также можно рассчитать по приближенной рекуррентной формуле с погрешностью приблизительно (3 – 5) % :

Ф(х) ≈ 1 – 0,65∙exp[-0,443(x +0,75)²].

5. Таблица соотношения энергетических спектров и функций корреляции

стационарных случайных процессов.

Таблица П.2.

В(τ)	W(ω)
π ∙ W0 ∙ δ(τ)	W0
exp (-α ∙ τ ), τ >0	2∙α / (α2 +ω2)
exp (-α ∙ τ2 ), τ >0	√π/α ∙ exp (-ω2/4α )
sin (Δω∙τ ) / ( Δω∙τ), τ >0	π / Δω , при 0 ≤ ω ≤ Δω; 0, при ω > Δω
exp (-α ∙ τ ) ∙ cos (ω0 ∙ τ ), τ >0	α / [α2+(ω-ω0)2]
exp (-α ∙ τ2 ) ∙ cos (ω0∙ τ ), τ >0	√π/4α ∙ exp[- (ω-ω 0)2/4α ]
[sin(Δω∙τ /2) / ( Δω∙τ/2)]∙cos(ω0∙τ) τ >0	π / Δω , при |ω-ω0| ≤ Δω/2; 0, при |ω-ω0| >Δω/2;

6. Таблицы функций Бесселя первого рода.

Таблица П.3

m Jк(m)	0,1	0,2	0,4	0,5	0,6	0,8
J0(m)	0,9975	0,99	0,0604	0,9385	0,912	0,8463	0,7652
J1(m)	0,0499	0,0995	0,196	0,2423	0,2867	0,3688	0,4401
J2(m)	0,0012	0,005	0,0197	0,0306	0,0437	0,0758	0,1149
J3(m)		0,0002	0,0013	0,0026	0,0044	0,0102	0,0196
J4(m)			0,0001	0,0002	0,0003	0,001	0,0025
J5(m)						0,0001	0,0002

Таблица П.4.

m Jк(m)	1,2	1,6
J0(m)	0,6711	0,4554	0,2239	- 0,26	- 0,397	- 0,178	0,15
J1(m)	0,4983	0,5699	0,5767	0,339	- 0,066	- 0,328	- 0,277
J2(m)	0,1593	0,257	0,3528	0,486	0,364	0,047	- 0,243
J3(m)	0,0329	0,0723	0,1289	0,309	0,43	0,365	0,115
J4(m)	0,005	0,015	0,024	0,132	0,281	0,391	0,358
J5(m)	0,0006	0,0025	0,007	0,043	0,132	0,261	0,362
J6(m)	0,0001	0,0003	0,001	0,011	0,049	0,131	0,246

Продолжение таблицы П.4.

J7(m)				0,003	0,015	0,053	0,13
J8(m)					0,004	0,018	0,57
J9(m)						0,006	0,021
J10(m)						0,001	0,007
J11(m)							0,002

Таблица П.5.

m Jк(m)
J0(m)	0,172	- 0,246	0,048	- 0,175	0,167
J1(m)	0,235	0,043	- 0,223	0,09	0,069
J2(m)	- 0,113	0,255	- 0,085	0,186	- 0,16
J3(m)	- 0,291	0,058	0,191	- 0,044	- 0,099
J4(m)	- 0,105	- 0,22	0,182	- 0,203	0,131
J5(m)	0,186	- 0,234	- 0,073	- 0,057	0,151
J6(m)	0,338	- 0,014	- 0,244	0,167	- 0,055
J7(m)	0,321	0,217	- 0,17	0,182	- 0,184
J8(m)	0,224	0,318	0,045	- 0,007	- 0,074
J9(m)	0,126	0,292	0,23	0,19	0,125
J10(m)	0,061	0,208	0,3	- 0,206	0,186
J11(m)	0,026	0,123	0,27	- 0,068	0,061
J12(m)	0,01	0,063	0,195	0,112	- 0,119
J13(m)	0,003	0,029	0,12	0,237	- 0,204
J14(m)	0,001	0,012	0,065	0,272	- 0,146
J15(m)		0,005	0,032	0,24	- 0,008
J16(m)		0,002	0,014	0,178	0,145
J17(m)			0,006	0,115	0,233
J18(m)			0,002	0,067	0,251
J19(m)				0,035	0,219
J20(m)				0,017	0,165
J21(m)				0,008	0,111
J22(m)				0,003	0,068
J23(m)				0,001	0,038
J24(m)					0,02
J25(m)					0,01
J26(m)					0,004

Примечания.

1. Значения функций Бесселя равные нулю означают не абсолютное их равенство нулю, а очень малую величину, которой можно пренебречь.

2. Отрицательные значения функций Бесселя говорят о начальной фазе этих составляющих равных 180⁰ (π радиан). Не показанные в таблице П.3 и П.4 значения J₆(m) – J₂₀(m) для m = 0,1 – 1 и J₁₂(m) – J₂₀(m) для m = 1,2 – 6 говорят о равенстве их нулю (вернее очень маленькой величине).

СПИСОК ЛИТЕРАТУРЫ

Основная:

1. В. Феллер Введение в теорию вероятностей и ее приложения, том-1,2- М.: Мир, 1984

2. Теория электрической связи / Зюко А.Г. и др. Под ред. Д.Д. Кловского. – М.: Радио и связь, 1998

3. Панфилов И.П., Дырда В.Е. Теория электрической связи. – М.: Радио и связь, 1991

4. Кловский Д.Д., Шилкин В.А. Теория электрической связи. Сборник задач и упражнений. – М.: Радио и связь, 1990

Дополнительная:

5. Баскаков С.И. Радиотехнические цепи и сигналы. – М.: Высшая школа, 1988

6. Гоноровский И.С. Радиотехнические цепи и сигналы. – М.: Радио и связь, 1994

7. Кловский Д.Д. Теория передачи сигналов. – М.: Связь, 1973

8. Зюко А.Г. и др. Теория передачи сигналов. – М.: Радио и связь, 1986

9. Емельянов Г.А., Шварцман В.О. Передача дискретной информации. – М.: Радио и связь, 1982

10. Баскаков С.И. Радиотехнические цепи и сигналы. Руководство к решению задач. – М.: Высшая школа, 1987

11. Радиотехнические цепи и сигналы. Примеры и задачи / Галустов Г.Г. и др. Под ред. И.С. Гоноровского. – М.: Радио и связь, 1989

12. Жуков В.П. и др. Задачник по курсу «Радиотехнические цепи и сигналы». – М.: Высшая школа, 1986

13. Кловский Д.Д., Шилкин В.А. Теория передачи сигналов в задачах. – М.: Связь, 1978

14. Справочник по специальным функциям с формулами, графиками и математическими таблицами. Под ред. М. Абрамовица и И. Стиган.- М.: Наука, 1979

15. Прудников А.П. и др. Интегралы и ряды. Элементарные функции. – М.: Наука, 1981