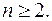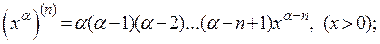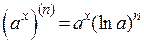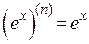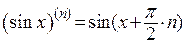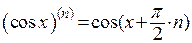Производные и дифференциалы высших порядков
1. Производные высших порядков. Если функция 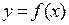 определена на некотором множестве X={x} и имеет производную
определена на некотором множестве X={x} и имеет производную 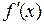 - некоторую функцию, определенную на Х, то производная от производной
- некоторую функцию, определенную на Х, то производная от производной 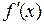 называется второй производной (производной второго порядка) и обозначается следующими символами:
называется второй производной (производной второго порядка) и обозначается следующими символами: 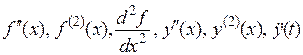 (если независимая переменная t – время, для физических приложений).
(если независимая переменная t – время, для физических приложений).
Высшие производные определяются по индукции. Производной n-го порядка (n-ой производной) функции 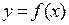 в точке х называется производная от производной (n–1)-го порядка
в точке х называется производная от производной (n–1)-го порядка
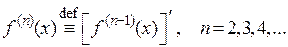 (1)
(1)
Производные высшего порядка иногда обозначают с помощью римских цифр: 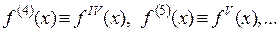
2. Основные правила вычисления n-ых производных.
1) 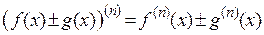 ;
;
2) 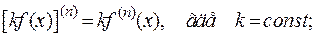
3) Формула Лейбница:
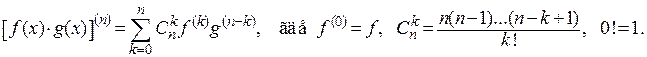
3. Производные n-го порядка от некоторых функций:
6. Дифференциалы высших порядков. Дифференциалом n-го порядка называется значение дифференциала d от дифференциала (n–1) порядка, когда приращение аргумента dx при вычислении очередного дифференциала равно приращению аргумента dx для предыдущего дифференциала. При этом очередной дифференциал вычисляется так же, как и первый дифференциал - как главная линейная часть приращения функции.
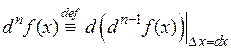 (1)
(1)
Если х - независимая переменная, то при этом условии справедливы формулы:
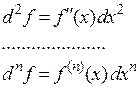 (2)
(2)
Откуда следует точное выражение для n-ой производной в дифференциальной форме, которое используется и как единый символ для обозначения n-ой производной:
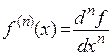 (3)
(3)
Если х не является независимой переменной, а является функцией какой-либо другой переменной, например t , то формулы (2)-(3) становятся неверными и высшие дифференциалы нужно находить из исходного определения по формуле (1). В частности при n=2 можно получить из (1):
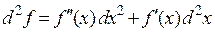 (4)
(4)
За счет появления второго слагаемого в формуле (4) второй дифференциал (2) и последующие дифференциалы являются не инвариантными относительно замены переменой.
Примеры решения задач
ПРИМЕР 1.Найти производную 2-го порядка от функции 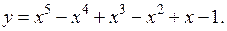
Решение.
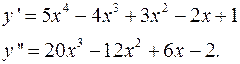
ПРИМЕР 2.Найти производную 2-го порядка от функции, заданной параметрически 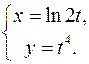
Решение.
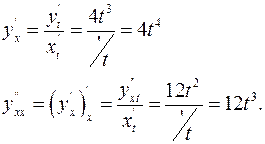
ПРИМЕР 3.Найти производные 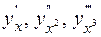 для функции
для функции 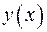 заданной параметрически:
заданной параметрически: 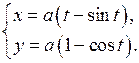
Решение.Для 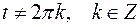 получим:
получим:
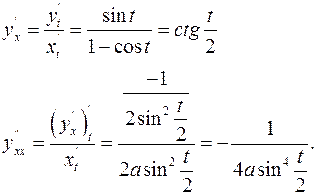
Аналогично находим 3-ю производную:
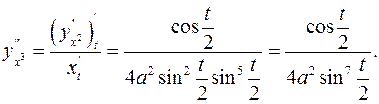
ПРИМЕР 4.Найти производную 2-го порядка от функции, заданной неявно 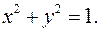
Решение. 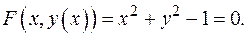 Воспользуемся формулой для нахождения производной, заданной неявно:
Воспользуемся формулой для нахождения производной, заданной неявно:

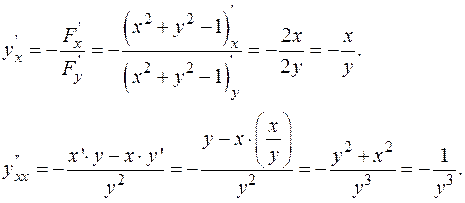
ПРИМЕР 5.Пусть функция 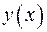 определяется из уравнения
определяется из уравнения 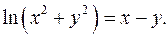 Найти
Найти 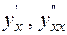 в точке с координатами
в точке с координатами 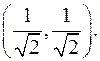
Решение.Дифференцируя данное соотношение, имеем
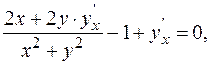 (1)
(1)
Откуда следует, что 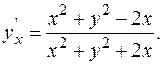 Следовательно,
Следовательно, 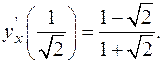 Вторую производную удобнее найти, предварительно перобразовав уравнение (1) к виду
Вторую производную удобнее найти, предварительно перобразовав уравнение (1) к виду 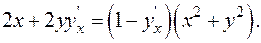
Получим 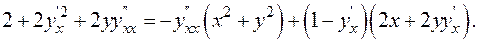
Решаем уравнение относительно 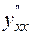 и подставляем в полученное выражение
и подставляем в полученное выражение 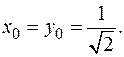 Тогда
Тогда 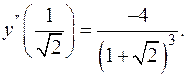
ПРИМЕР 6.Найти (n)-ю производную от функции 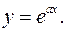
Решение. 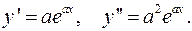 Продолжая операции дифференцирования, для (n)-ой производной получим
Продолжая операции дифференцирования, для (n)-ой производной получим 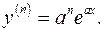
ПРИМЕР 7.Найти дифференциал 2-го порядка функции 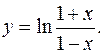
Решение.
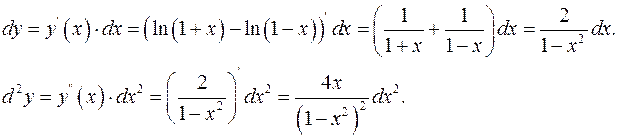
ПРИМЕР 8.Найти дифференциал (n)-го порядка функции 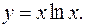
Решение.
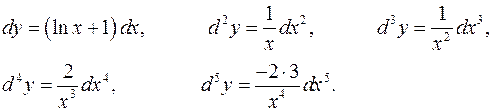
Теперь можно увидеть, как изменяются коэффициенты с увеличением порядка дифференциала и для (n)-го дифференциала получить формулу 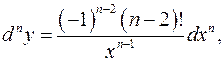 которая верна при
которая верна при