Методические рекомендации и примеры решения задач
a) При определении кинематических характеристик точки по заданному закону ее движения необходимо:
- определить систему отсчета, в которой задано движение;
- записать в общем виде формулы, определяющие искомые кинематические характеристики точки;
- определить значение кинематических характеристик по заданному закону движения точки.
При решении задач по определению кинематических характеристик тела и его точек необходимо:
- определить тип движения тела;
- записать в общем виде формулы искомых кинематических характеристик;
- определить значение кинематических характеристик по заданному закону движения тела.
При определении кинематических характеристик механической системы, включающей твердые и гибкие тела:
- построить схему механической системы;
- определить типы движения тел, входящих в систему. Отметить точки контакта, в которых движение от одного тела передается другому телу;
- определить кинематические характеристики точки тела, движение которого задано. Показать найденные кинематические характеристики на схеме;
 - определить кинематические характеристики других тел и их точек в той последовательности, в которой передается движение. Необходимо учитывать, что при передаче движения от одного тела другому без скольжения, точки контакта, принадлежащие одному и другому телу, имеют одинаковые скорости.
- определить кинематические характеристики других тел и их точек в той последовательности, в которой передается движение. Необходимо учитывать, что при передаче движения от одного тела другому без скольжения, точки контакта, принадлежащие одному и другому телу, имеют одинаковые скорости.
б) При решении задач динамики точки следует придерживаться следующего порядка действий:
- по условиям задачи определить к первому или второму основному типу относится задача;
- проанализировать условия задачи и выбрать метод решения: с помощью дифференциальных уравнения, общих терем или других принципов механики;
- построить расчетную схему: изобразить на чертеже рассматриваемый объект в промежуточном положении на траектории, обозначить систему координат, показать действующие на объект силы;
- записать в общем (алгебраическом) виде формулу выбранного метода решения;
- составить и решить уравнение (или систему уравнений) в соответствии с действующей системой сил.
Примеры решения задач
Пример 1.Движение точки М в плоскости ХУ задано уравнениями:
X = 4sin 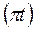 , (1)
, (1)
Y = 3cos 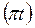 , (2)
, (2)
где Х и У выражены в сантиметрах, t - в секундах.
Найти и изобразить на чертеже траекторию, скорость и ускорение точки в момент времени t1 = 1с.
Решение:
1. Движение точки задано в координатной системе отсчета.
2. Уравнение траектории точки в координатах ХУ имеет вид Y=f(X). Чтобы получить указанную зависимость, следует исключить время t из уравнений движения. Так как параметр t входит в аргументы тригонометрических функций, целесообразно исключить параметр t в составе тригонометрических функций.
Выразим из уравнений (1),(2) значения синуса и косинуса через координаты Х,У.
Sin 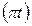 =
= 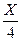 ;
; 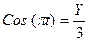 (3)
(3)
Подставим найденные значения тригонометрических функций (3) в тригонометрическое тождество вида Sin2 α +Cos2 α=1
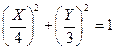 (4)
(4)
Полученное выражение (4) является уравнением эллипса с полуосями по оси Х = 4 см., по оси У =3 см.
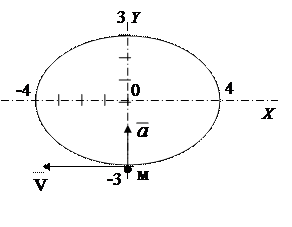 График траектории построим по характерным точкам (рис.1).
График траектории построим по характерным точкам (рис.1).

Рис. 1
Положение точки на траектории при t1=1с определим по значениям координат точки
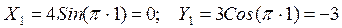 см.
см.
3. Скорость точки при координатном способе задания определяется по формулам
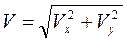 (5)
(5)
где 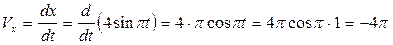 , см/с;
, см/с;
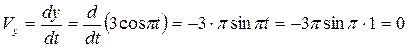 , см/с
, см/с
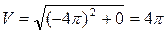 , см/с
, см/с
4. Ускорение точки

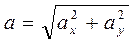 , (6)
, (6)
где 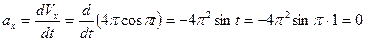
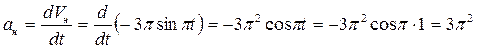 ,см/с2
,см/с2
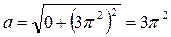 , см/с2
, см/с2
Ответ: уравнение траектории 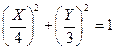 , V=4 π см/c, a= 3 π2 см/с2
, V=4 π см/c, a= 3 π2 см/с2
Пример 2. Груз 1 движется согласно уравнению х= kt2, где k постоянное число. Определить в алгебраической форме скорость точки С и угловую скорость катка 3. Каток перемещается по неподвижной направляющей без скольжения ( рис.2.1).
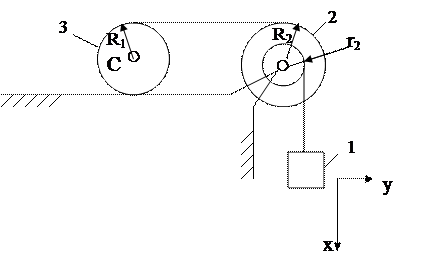 |
Рис.2.1
Решение:
1. Расчетная схема механической система приведена на рис.2.2
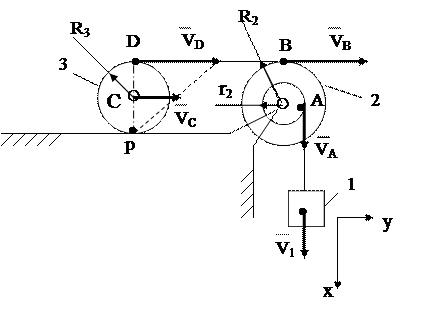 |
Рис.2.2
2. Тела совершают движение: груз 1- поступательное; шкив 2 – вращательное вокруг неподвижной оси; каток 3 – плоско-параллельное.
| |
3. Скорость груза 1, совершающего поступательное движение
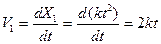

4. Скорость точки А шкива 2
VA=V1=2kt
5. Угловая скорость шкива 2
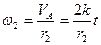
6. Скорость точки В шкива 2
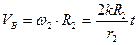
7. Скорость точки D катка 3
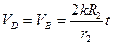
8. Угловая скорость катка 3, совершающего плоское движение
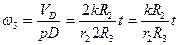
Точка Р – мгновенный центр вращения.
9. Скорость точки С
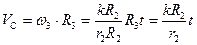
Ответ: 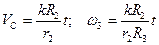
Пример 3. Движение свободной материальной точки весом 2 г выражается уравнениями:
х = 3 cos 2 p t, y = 4 sin p t,
где t выражено в секундах, х,у - в метрах.
Определить проекции силы, действующей на точку, в зависимости от ее координат.
Решение:
1.Задача относится к первому основному типу типу задач динамики: определение действующих сил при заданном законе движения точки.
2. Решим задачу на основании основного закона динамики
Fх= m aх , Fу= m aу , (1)
где m – масса точки, aх , aу – проекции ускорения точки на оси х, у.
3. Находим проекции ускорения точки на оси координат путем дифференцирования уравнений движения
Vx = 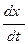 = - 6 p sin 2 p t Vy =
= - 6 p sin 2 p t Vy = 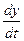 = 4 p cos p t
= 4 p cos p t
ax = 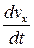 = - 12 p2 cos p t = - 4 p2 x , ay =
= - 12 p2 cos p t = - 4 p2 x , ay = 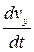 = - 4 p2 sin p t = - p2 y
= - 4 p2 sin p t = - p2 y
На основании уравнений (1) находим проекции силы, действующей на точку, в зависимости от ее координат.
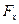 = m ax =
= m ax = 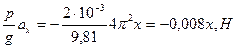
Fy = m ay = 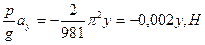

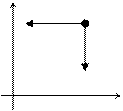 |
Рис.3
Ответ: Fx= - 0,008х,Н, Fу= - 0,002у,Н.
Пример 4. Тело массой m начинает двигаться под действием силы тяжести по негладкой плоскости наклоненной под углом l к горизонту. Коэффициент трения скольжения равен ¦.
Определить скорость тела через t секунд после начала движения.
Решение:
1. Задача относится ко второму основному типу: определение кинематических характеристик при заданных действующих силах.Движение тела будем рассматривать как движение материальной точки, так как оно совершает поступательное движение. Решим задачу с применением дифференциального уравнения вида
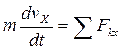 (1)
(1)
2. Изображаем тело в промежуточном положении на траектории. Ось координат х направляем по линии движения груза, начало координат помещаем в точке, соответствующей начальному положению тела (Х0=0). Показываем действующие на тело внешние силы (рис.4): силу тяжести 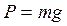 , нормальную реакцию плоскости
, нормальную реакцию плоскости 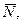 силу трения
силу трения 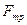 .
.
Силу тяжести разложим на составляющие, параллельные осям координат.
 | |||
| | |||
Рис.4
3. Составим дифференциальное уравнение движения груза в соответствии с выражением (1)
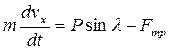 (2)
(2) 
Сила трения 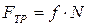 . Cилу N определим из условия: при перемещении тела его координата У не изменяется, следовательно сумма проекций сил на ось У равна нулю
. Cилу N определим из условия: при перемещении тела его координата У не изменяется, следовательно сумма проекций сил на ось У равна нулю
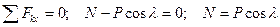 .
. 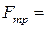 ƒPcosλ
ƒPcosλ
Уравнение (2) примет вид
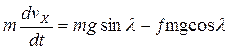 (3)
(3)
Решим уравнение (2) методом разделения переменных

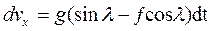 (4)
(4)
Проинтегрируем выражение (4)
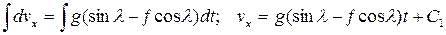 (5)
(5)
Постоянную интегрирования С1 определим из начальных условий: t=0, vx=0. После подстановки этих значений в уравнение (5), получим С1=0.
Ответ: 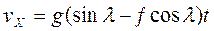
Пример 5. Решить пример 4 с применением общей теоремы динамики.
Решение:
1. Задача относится ко второму основному типу задач динамики.
2. Анализ условий задачи и выбор метода решения.
Из условий задачи известны: начальная скорость тела, действующие на тело силы (сила тяжести, сила трения), время действия сил (время движения тела). Движение тела будем рассматривать, как движение материальной точки, так как оно совершает поступательное движение. При этих условиях конечную скорость тела удобно определить на основании теоремы об изменении количества движения материальной точки.
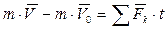 (1)
(1)
где mV –количество движения точки в конечный момент времени;
mV0–количество движения точки в начальный момент времени;
Fkּ t – импульс k-той силы.
2. Изображаем движущееся тело в промежуточном положении на траектории и показываем действующие на него внешние силы (рис.5): силу тяжести 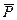 , нормальную реакцию плоскости
, нормальную реакцию плоскости 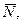 силу трения. Сила трения равна произведению коэффициента трения на силу нормального давления
силу трения. Сила трения равна произведению коэффициента трения на силу нормального давления 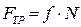 . Силу нормального давления определим из условия: координата У при движении тела не изменяется, следовательно
. Силу нормального давления определим из условия: координата У при движении тела не изменяется, следовательно 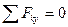 .
.
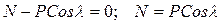
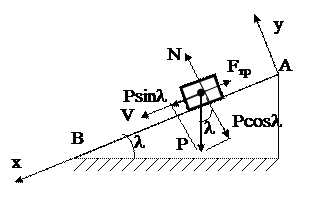 |
Рис.5
Запишем равенство (1) в проекции на ось Х
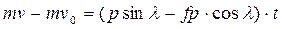 (2)
(2)
После подставки в уравнение (2) значений p=mg, v0 = 0 получим выражение, определяющее скорость точки 
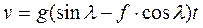
Ответ: 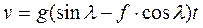
Пример 6. Вертикальный вал AВ (рис.6), вращающийся с постоянной угловой скоростью 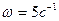 , закреплен в точке А при помощи подпятника, а в точке В - при помощи цилиндрического подшипника. В точке Д к валу под углом
, закреплен в точке А при помощи подпятника, а в точке В - при помощи цилиндрического подшипника. В точке Д к валу под углом 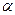 жестко прикреплен однородный стержень с точечной массой m = 2 кг на конце стержня в точке Е. Длина стержня
жестко прикреплен однородный стержень с точечной массой m = 2 кг на конце стержня в точке Е. Длина стержня 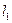 = 0,6м. Определить реакции опор А и В, если АД = а, ДВ = 2а,
= 0,6м. Определить реакции опор А и В, если АД = а, ДВ = 2а, 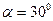 , а = 0,5 м. Массой стержней пренебречь.
, а = 0,5 м. Массой стержней пренебречь.
Решение:
1. Задача относится к первому основному типу задач динамики: задано движение тела, требуется определить силы, действующие на тело.
2. Анализ условий задачи и выбор метода решения.
Из условий задачи известны размеры тела и скорость его вращения, следовательно, могут быть определены его кинематические характеристики. На тело действует сила тяжести груза и реакции связей А и В. При этих условиях реакции связей удобно определять на основании принципа Даламбера
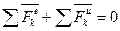 ,
,
где 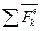 - сумма внешних сил,
- сумма внешних сил, 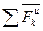 -сумма сил инерции.
-сумма сил инерции.
3. Расчетная схема.
Покажем на схеме (рис.6) активные силы , реакции связей и силу инерции груза: 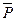 - сила тяжести точечной массы;
- сила тяжести точечной массы; 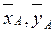 - составляющие реакции опоры А;
- составляющие реакции опоры А; 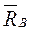 - реакция опоры В,
- реакция опоры В, 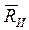 = сила инерции груза.
= сила инерции груза.

Рис.6
4. Составим уравнения равновесия
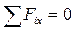 ;
; 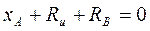 , (1)
, (1)
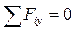 ;
; 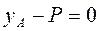 , (2)
, (2)
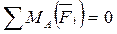 ;
; 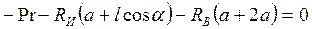 . (3)
. (3)
5. Решим полученную систему уравнений.
Сила тяжести груза 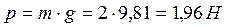 .
.
Сила инерции груза RИ=ma. Вал вращается с постоянной скоростью, поэтому тангенциальное ускорение груза равно нулю, а нормальное ускорение равно 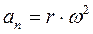 , где
, где 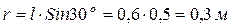 - кратчайшее расстояние от груза до оси вращения. Ускорение направлено к оси вращения, сила инерции – от оси вращения. Значение силы инерции
- кратчайшее расстояние от груза до оси вращения. Ускорение направлено к оси вращения, сила инерции – от оси вращения. Значение силы инерции
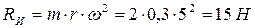
Из уравнения (3):
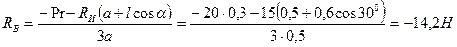
Из уравнения (1):
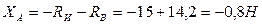
Из уравнения (2):
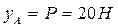
Ответ: 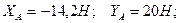
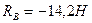 .
.
Знак минус в значении реакций означает, что эти реакции имеют направление, противоположное показанному на рис.6.
Индивидуальные задания
Задача 1.Движение точки М в плоскости ХУ задано уравнениями
X = 2t+1, (1) ; Y = 3t2 , (2),
где Х и У выражены в метрах, t - в секундах.
Найти и изобразить траекторию точки , определить скорость, касательное, нормальное и полное ускорение в момент времени t1, а так же радиус кривизны в соответствующей точке траектории. Показать на чертеже положение точки в момент времени t1 = 1с.
Задача 2. Механизм состоит из колеса 1 с радиусом R1=0,1м ,ступенчатого колеса 2 с радиусами R2=0,2м , r2=0,1м и колеса 3 с радиусом R3=0,3м (рис.7). Колеса находятся в зацеплении или связанны гибкой передачей.
По заданному уравнению вращательного движения колеса 1 φ1 = 0,3(2t2 +5t) определить скорости вращения колес 1 и 2, а также полное ускорение точки М в момент t=2с.
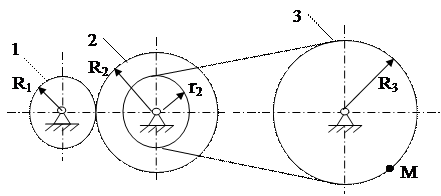
Рис.7
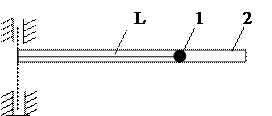
Задача 3.Груз 1 массой m находится внутри трубки 2 и связан с осью вращения нитью длиной L (рис.8). Трубка вращается вокруг вертикальной оси с постоянной угловой скоростью ω. Определить натяжение нити.
 | |||
| | |||
Рис.8
Задача 4. На тело массой m, находящегося на горизонтальной поверхности, действует переменная по модулю сила F=kt, направленная параллельно поверхности (k – постоянная величина). Коэффициент трения скольжения ƒ.
Определить закон движения тела.
| |
Задача 5. Санки, пущенные скользить по горизонтальной поверхности льда, останавливаются через 10 секунд.
Найти начальную скорость санок, если коэффициент трения f = 0,07.
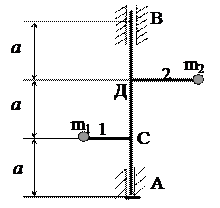
Задача 6.Вертикальный вал AВ (рис.9), вращающийся с постоянной угловой скоростью 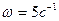 , закреплен в точке А при помощи подпятника, а в точке В - при помощи цилиндрического подшипника. В точках С и Д к валу жестко прикреплены стержни с точечными массами m1 = 2 кг, m2=3кг на концах стержней. Длины стержней
, закреплен в точке А при помощи подпятника, а в точке В - при помощи цилиндрического подшипника. В точках С и Д к валу жестко прикреплены стержни с точечными массами m1 = 2 кг, m2=3кг на концах стержней. Длины стержней 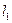 = 0,3м,
= 0,3м, 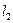 = 0,6м. Определить реакции опор А и В, если АС=СД =ДВ= а = 0,5 м. Массой вала и стержней пренебречь.
= 0,6м. Определить реакции опор А и В, если АС=СД =ДВ= а = 0,5 м. Массой вала и стержней пренебречь.
 | |||
| | |||
Рис.9
