Примеры для самостоятельного решения. Методические рекомендации
Методические рекомендации
По выполнению контрольной работы по теме
«Элементы операционного исчисления»
Для студентов 2-3 курсов вечерне-заочного факультета
Мурманск 2015
Составитель – Хохлова Людмила Ивановна, доцент кафедры высшей математики и программного обеспечения МИС и ПО МГТУ
Методические рекомендации рассмотрены и одобрены кафедрой
_______________ 2015 г., протокол №
Рецензент – Р. А. Богомолов, канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения МИС и ПО МГТУ МГТУ
Оглавление
Оглавление
§ 1. Оригиналы . 4
§ 2. Единичная функция Хэвисайда. Запись оригиналов с помощью функции Хэвисайда. 5
§ 3. Преобразование Лапласа. Изображение оригинала. Основные свойства изображения. 8
§4. Применение теоремы запаздывания для нахождения изображений запаздывающих процессов. 11
§5. Изображение кусочно - непрерывных функций. 13
§ 6. Применение теорем о дифференцировании оригинала и изображения для нахождения изображений. 18
§ 7. Изображение интеграла от оригинала. Теорема об интегрировании оригинала. 19
§ 8. Изображение периодического оригинала. 20
§9. Свертка. Изображение свертки. 23
§ 10.Восстановление оригиналов по изображению. 25
П.2 Восстановление оригиналов с помощью свертки. 26
П.4. Нахождение оригиналов с помощью теоремы запаздывания. 29
§ 11. Применение операционного исчисления к решению линейных дифференциальных уравнений с постоянными коэффициентами. 30
§ 12. Применение операционного исчисления к решению систем линейных дифференциaльных уравнений. 32
Таблица оригиналов и изображений. 34
Таблица сверток оригиналов. 35
Образец решения контрольной работы. 38
Задания контрольной работы.. 40
Оригиналы.
Определение.Оригиналомназывается любая однозначная функция 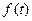 действительной переменной
действительной переменной 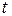 , определённая на всей числовой прямой и удовлетворяющая условиям:
, определённая на всей числовой прямой и удовлетворяющая условиям:
1) 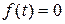 при
при 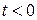 ;
;
2) 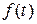 кусочно- непрерывна при
кусочно- непрерывна при 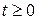 ;
;
3) 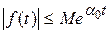 , где
, где 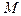 и
и 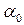 - постоянные,
- постоянные, 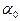 называется показателем роста функции
называется показателем роста функции 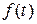 .
.
Примеры. Установить какие из функций являются оригиналами и найти для них показатели роста : 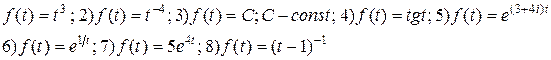
Замечание. Будем считать, что условие 1) выполняется для всех функций, т.к. это соответствует реальным физическим задачам.
Решение.
1) 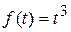 — является оригиналом, т.к. функция непрерывна на всей числовой прямой и
— является оригиналом, т.к. функция непрерывна на всей числовой прямой и 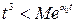 начиная с некоторого t, причем
начиная с некоторого t, причем 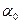 -любое положительное действительное число;
-любое положительное действительное число;
2) 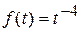 — оригиналом не является, т.к. имеет в точке t =0 бесконечный разрыв;
— оригиналом не является, т.к. имеет в точке t =0 бесконечный разрыв;
3) 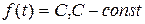 — оригинал ,
— оригинал , 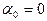 т.к.
т.к. 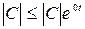 ;
;
4) 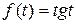 — оригиналом не является, т.к. имеет точки бесконечного разрыва; 5)
— оригиналом не является, т.к. имеет точки бесконечного разрыва; 5) 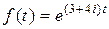 является оригиналом, т.к. функция непрерывна на всей числовой прямой и
является оригиналом, т.к. функция непрерывна на всей числовой прямой и 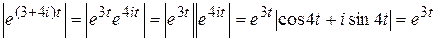 , т.е.
, т.е. 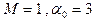 ;
;
6) 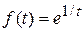 — оригиналом не является, т.к. имеет в точке
— оригиналом не является, т.к. имеет в точке 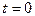 бесконечный разрыв;
бесконечный разрыв;
7) 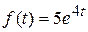 — оригинал, т.к. функция непрерывна на всей числовой прямой и
— оригинал, т.к. функция непрерывна на всей числовой прямой и 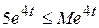 , т.е.
, т.е. 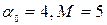 ;
;
8) 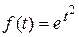 — оригиналом не является, т.к. не выполняется условие 3) для этой функции.
— оригиналом не является, т.к. не выполняется условие 3) для этой функции.
Вопросы для самопроверки.
1. Дайте определение оригинала
2. Дайте определение показателя роста оригинала
Примеры для самостоятельного решения.
Установить являются ли следующие функции оригиналами :
1) 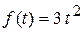 ; 2)
; 2) 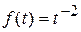 ; 3)
; 3) 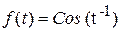 ; 4)
; 4) 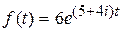 ; 5)
; 5) 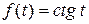 ;6)
;6) 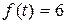 ;7)
;7) 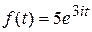 ;8)
;8) 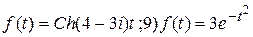 Ответы: 1) да,
Ответы: 1) да, 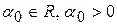 ; 2) нет; 3) нет; 4) да,
; 2) нет; 3) нет; 4) да, 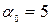 ; 5) нет ; 6) да,
; 5) нет ; 6) да, 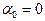 ; 7) да,
; 7) да, 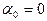 ; 8) да ,
; 8) да , 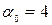 ; 9) да,
; 9) да, 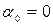 .
.
