Задача 47

Знайти лінію, яка проходить через точку М₀ і має таку властивість: в кожній точці М нормальний вектор 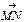з кінцевою точкою на осі Оу має довжину а, і утворює гострий кут з додатним напрямком осі Оу.

1. М₀ (15, 1), а = 25.
2. М₀ (12, 2), а = 20.
3. М₀ (9, 3), а = 15.
4. М₀ (6 ,4), а = 10.
5. М₀ (3, 5), а = 5.

Знайти лінію, яка проходить через точку М₀, якщо відрізок кожної її нормалі, що міститься між осями координат, ділиться точкою лінії в співвідношенні а:b (відраховуючи від осі Оу).

1. М₀ (1, 1), а:b = 1:2.
2. М₀ (–2, 3), а:b = 1:3.
3. М₀ (0, 1), а:b = 2:3.
4. М₀ (1, 0), а:b = 3:2.
5. М₀ (2, –1), а:b = 3:1.

Знайти лінію, яка проходить через точку М₀, якщо відрізок кожної її дотичної, що міститься між точкою дотику і віссю Оу делиться в точці перетину с віссю абсцис в співвідношенні а:b (відраховуючи від осі Оу).

11. М₀ (2, –1), а:b = 1:1.

1. М₀ (1, 2), а:b= 2:1.
2. М­₀ (–1, 1), а:b = 3:1.
3. М₀ (2, 1), а:b= 1:2.
4. М₀ (1, –1), а:b=1:3.

Знайти лінію, яка проходить через точку М₀, якщо відрізок кожної її дотичної, що міститься між осями координат, делиться в точці дотику в співвідношенні а:b (відраховуючи від осі Оу).

16. М₀ (1, 2), а:b = 1:1.

17. М₀ (2, 1), а:b= 1:2.

18. М₀ (1, 3), а:b = 2:1.

19. М₀ (2, –3), а:b = 3:1.

20. М₀ (3, –1), а:b=3:2.

Знайти лінію, яка проходить через точку М₀ і має таку властивість: в кожній точці М дотичний вектор 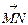з кінцевою точкою на осі Оу має проекцію на ось Ох, обернено пропорційно абсцисі точки М. Коефіциєнт пропорційності дорівнює а.

21. М₀ (1, е), а = –1/2.

22. М₀ (2, е), а = –2.

23. М₀ (–1, 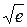), а = –1.

24. М₀ (2, 1/е), а = 2.

25. М₀ 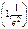, а = 1/4.

Знайти лінію, яка проходить через точку М₀ і має таку властивість: в кожній точці М дотичний вектор 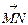з кінцевою точкою на осі Оу має проекцію на ось Оу, яка дорівнює а.

26. М₀ (1, 2), а = –1.

27. М₀ (1, 4), а = 2.

28. М₀ (1, 5), а = –2.

29. М₀ (1, 3), а = –4.

30. М₀ (1, 6), а = 3.

31. М₀ (1, 1), а = 1.