Линейная зависимость и независимость векторов
Пусть L – линейное пространство над полем Р. Пусть а1, а2, … , аn (*) конечная система векторов из L. Вектор в = a1×а1 + a2×а2 + … + an×аn ( 16) называется линейной комбинацией векторов (*), или говорят, что вектор в линейно выражается через систему векторов (*).
Определение 14. Система векторов (*) называется линейно зависимой, тогда и только тогда, когда существует такой ненулевой набор коэффициентов a1, a2, … , an, что a1×а1 + a2×а2 + … + an×аn = 0. Если же a1×а1 + a2×а2 + … + an×аn = 0 Û a1 = a2 = … = an = 0, то система (*) называется линейно независимой.
Свойства линейной зависимости и независимости.
10. Если система векторов содержит нулевой вектор, то она линейно зависима.
Действительно, если в системе (*) вектор а1 = 0, то 1×0 + 0×а2 + … + 0×аn = 0.
20. Если система векторов содержит два пропорциональных вектора, то она линейно зависима.
Пусть а1 = l×а2. Тогда 1×а1 –l×а2 + 0×а3 + … + 0×аn = 0.
30. Конечная система векторов (*) при n ³ 2 линейно зависима тогда и только тогда, когда хотя бы один из её векторов является линейной комбинацией остальных векторов этой системы.
Þ Пусть (*) линейно зависима. Тогда найдётся ненулевой набор коэффициентов a1, a2, … , an, при котором a1×а1 + a2×а2 + … + an×аn = 0 . Не нарушая общности, можно считать, что a1 ¹ 0. Тогда существует 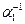 и а1 =
и а1 = 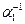 ×a2×а2 + … +
×a2×а2 + … + 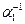 ×an×аn. Итак, вектор а1 является линейной комбинацией остальных векторов.
×an×аn. Итак, вектор а1 является линейной комбинацией остальных векторов.
Ü Пусть один из векторов (*) является линейной комбинацией остальных. Можно считать, что это первый вектор, т.е. а1 = b2а2 + … + bnаn, Отсюда (–1)×а1 + b2а2 + … + bnаn = 0, т.е. (*) линейно зависима.
Замечание. Используя последнее свойство, можно дать определение линейной зависимости и независимости бесконечной системы векторов.
Определение 15. Система векторов а1, а2, … , аn , … (**) называется линейно зависимой, если хотя бы один её вектор является линейной комбинациейнекоторого конечного числа остальных векторов. В противном случае система (**) называется линейно независимой.
40. Конечная система векторов линейно независима тогда и только тогда, когда ни один из её векторов нельзя линейно выразить через остальные её векторы.
50. Если система векторов линейно независима, то любая её подсистема тоже линейно независима.
60. Если некоторая подсистема данной системы векторов линейно зависима, то и вся система тоже линейно зависима.
Пусть даны две системы векторов а1, а2, … , аn , … (16) и в1, в2, … , вs, … (17). Если каждый вектор системы (16) можно представить в виде линейной комбинации конечного числа векторов системы (17), то говорят, что система (17) линейно выражается через систему (16).
Определение 16. Две системы векторов называются эквивалентными, если каждая из них линейно выражается через другую.
Теорема 9 (основная теорема о линейной зависимости).
Пусть 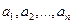 и
и 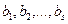 – две конечные системы векторов из L. Если первая система линейно независима и линейно выражается через вторую, то n £ s.
– две конечные системы векторов из L. Если первая система линейно независима и линейно выражается через вторую, то n £ s.
Доказательство. Предположим, что n > s. По условию теоремы
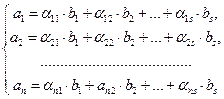 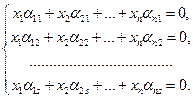 (21) (21) | Так как система 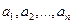 линейно независима, то равенство линейно независима, то равенство 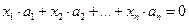 (18) Û х1=х2=…=хn= 0. Подставим сюда выражения векторов (18) Û х1=х2=…=хn= 0. Подставим сюда выражения векторов 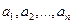 : : 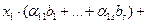 …+ …+ 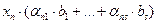 =0 (19). Отсюда =0 (19). Отсюда 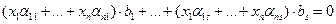 (20). Условия (18), (19) и (20), очевидно, эквивалентны. Но (18) выполняется только при х1=х2=…=хn= 0. Найдём, когда верно равенство (20). Если все его коэффициенты равны нулю, то оно, очевидно, верно. Приравняв их нулю, получим систему (21). Так как эта система имеет нулевое решение, то она (20). Условия (18), (19) и (20), очевидно, эквивалентны. Но (18) выполняется только при х1=х2=…=хn= 0. Найдём, когда верно равенство (20). Если все его коэффициенты равны нулю, то оно, очевидно, верно. Приравняв их нулю, получим систему (21). Так как эта система имеет нулевое решение, то она |
совместна. Так как число уравнений больше числа неизвестных, то система имеет бесконечно много решений. Следовательно, у неё есть ненулевое решение х10, х20, …, хn0. При этих значениях равенство (18) будет верно, что противоречит тому, что система векторов 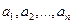 линейно независима. Итак, наше предположение не верно. Следовательно, n £ s.
линейно независима. Итак, наше предположение не верно. Следовательно, n £ s.
Следствие. Если две эквивалентные системы векторов конечны и линейно независимы, то они содержат одинаковое число векторов.
Определение 17. Система векторов называется максимальной линейно независимой системой векторов линейного пространства L, если она линейно независима, но при добавлении к ней любого вектора из L , не входящего в эту систему, она становится уже линейно зависимой.
Теорема 10. Любые две конечные максимальные линейно независимые системы векторов из L содержат одинаковое число векторов.
Доказательство следует из того, что любые две максимальные линейно независимые системы векторов эквивалентны.
Легко доказать, что любую линейно независимую систему векторов пространства L можно дополнить до максимальной линейно независимой системы векторов этого пространства.
Примеры:
1. Во множестве всех коллинеарных геометрических векторов любая система, состоящая их одного ненулевого вектора, является максимальной линейно независимой.
2. Во множестве всех компланарных геометрических векторов любые два неколлинеарных вектора составляют максимальную линейно независимую систему.
3. Во множестве всех возможных геометрических векторов трёхмерного евклидова пространства любая система трёх некомпланарных векторов является максимальной линейно независимой.
4. Во множестве всех многочленов степени не выше n с действительными (комплексными) коэффициентами система многочленов 1, х, х2, … , хn является максимальной линейно независимой.
5. Во множестве всех многочленов с действительными (комплексными) коэффициентами примерами максимальной линейно независимой системы являются
а) 1, х, х2, … , хn, … ;
б) 1, (1 – х), (1 – х)2, …, (1 – х)n, …
6. Множество матриц размерности m´n является линейным пространством (проверьте это). Примером максимальной линейно независимой системы в этом пространстве является система матриц Е11 = 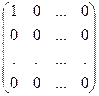 , Е12 =
, Е12 = 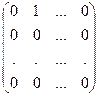 , … , Еmn =
, … , Еmn = 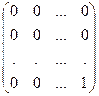 .
.
Пусть дана система векторов с1, с2, … , ср (*). Подсистема векторов из (*) называется максимальной линейно независимой подсистемой системы (*), если она линейно независима, но при добавлении к ней любого другого вектора этой система она становится линейно зависимой. Если система (*) конечна, то любая её максимальная линейно независимая подсистема содержит одно и то же число векторов. (Доказательство проведите самостоятельно). Число векторов в максимальной линейно независимой подсистеме системы (*) называется рангом этой системы. Очевидно, эквивалентные системы векторов имеют одинаковые ранги.
