Следствия теоремы Больцано-Коши

1. Теорема о нуле непрерывной функции.

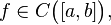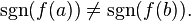Если функция непрерывна на некотором отрезке и на концах этого отрезка принимает значения противоположных знаков, то существует точка, в которой значение функции равно нулю. Формально: пусть и Тогда 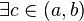такое, что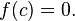

2. В частности любой многочлен нечётной степени имеет, по меньшей мере, один нуль.

Иногда теорему о нуле непрерывной функции называют первой теоремой Больцано-Коши, а теорему о промежуточном значении - второй теоремой соответственно. Хотя на самом деле эти теоремы эквивалентны.

18 Первая и вторая теорема вейерштрасса.

Теорема (первая теорема Вейерштрасса)

Если функция непрерывна на сегменте, то она ограничена на нем.

Доказательство: методом от противного, воспользуемся свойством замкнутости сегмента [a;b]. Из любой последовательности (xn) этого сегмента можем выделить подпоследовательность xnk, сходящуюся к x0∈[a;b] .

Пусть f не ограничена на сегменте [a;b], например, сверху, тогда для всякого натуральногоn∈N найдется точка xn∈[a;b] , что f(xn)>n. Придавая n значения 1,2,3,{\ldots}, мы получим последовательность (xn)точек сегмента [a;b], для которых выполнено свойство f(x1)>1,f(x2)>2,f(x3)>3,...,f(xn)>n...

Последовательность (xn) ограничена и поэтому из нее по теореме можно выделить подпоследовательность(xnk), которая сходится к точке x0∈[a;b] : limk→∞xnk=x0 (1)

Рассмотрим соответствующую последовательность (f(xnk)). С одной стороны f(xnk)>nk и поэтому limk→∞f(xnk)=+∞ (2),

С другой стороны, учитывая определение непрерывной функции по Гейне из (1) будем иметьlimk→∞f(xnk)=f(x0) (3)
Получаем равенства (2) и (3) противоречат теореме (о единственности предела). Это противоречие и доказывает справедливость теоремы. Аналогично доказывается ограниченность функции снизу. Ч.Т.Д.

Замечание 1
Таким образом, если f непрерывна на [a;b], то ее множество значений ограничено и поэтому существует конечные верхняя и нижняя грань функции.

c=infx∈[a;b]f(x),d=supx∈[a;b]f(x), но открыт вопрос о достижении
функции своих граней.

Замечание 2
Если слово сегмент в условии теоремы заменить словом интервал или полуинтервал, то теорема может и нарушиться. Пример, y=tgx,tgx∈C((−2π;2π)) , но функция не ограничена на этом интервале.

Теорема (вторая теорема Вейерштрасса)

Если функция непрерывна на сегменте, то она достигает на нем своих граней (т.е. непрерывная на сегменте функция принимает свое наибольшее и наименьшее значения).

Доказательство: Пусть f(x)∈C([a;b]) , c=infx∈[a;b]f(x), d=supx∈[a;b]f(x). По первой
теореме Вейерштрасса c,d∈R . Докажем, что f достигает на [a;b] своих граней, т.е. найдутся такие точки x1,x2∈[a;b] , чтоf(x1)=c,f(x2)=d.

Докажем, например, существование точки x2.

По определению верхней грани имеем (∀x∈[a;b])(f(x)=d) . Предположим противное, т.е. точки x2, в которой f(x2)=dна [a;b], тогда на [a;b] выполняется условиеf(x)<d или d−f(x)>0 . Далее введем вспомогательную функцию ϕ(x)=1d−f(x) . ϕ(x) на [a;b] положительна и непрерывна (как отношение двух непрерывных на [a;b] функций и d−f(x)/=0) , поэтому по первой Т. Вейерштрасса ϕ(x) на [a;b]ограничена.
Это означает, что при некотором М>0 (∀x∈[a;b])(0<1d−f(x)≤M) , отсюда имеем f(x)≤d−1M<d .
Полученное неравенство противоречит тому, что d является верхней гранью функции f(x) на [a;b], т.е. наименьшим из верхних границ. Полученное противоречие и означает существование точки x2 такой, чтоf(x2)=d.

Аналогично доказывается существование точки x1∈[a;b] , такой что f(x1)=c.

Следствие
Если f непрерывна и непостоянна на [a;b], то образ этого отрезка [a;b] при отображении f будет так же отрезок, т.е. непрерывный непостоянный образ отрезка есть отрезок.

Доказательство: В самом деле образом отрезка [a;b] при отображении f будет отрезок [с;d], где c=inf[a;b]f(x)=min[a;b]f(x), а d=sup[a;b]f(x)=max[a;b]f(x), что следует из второй теоремы Больцано-Коши и второй теоремы Вейерштрасса Ч.Т.Д.

19 Производная функции в точке. Геометрический смысл производной.

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной —интегрирование.

Определение

Пусть в некоторой окрестности точки 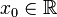определена функция 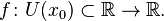Производной функции называется такое число 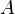, что функцию в окрестности 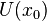можно представить в виде

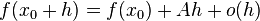
если 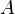существует.