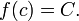Больцано-Коши и Вейерштрасса (без доказательства)

1) Определение односторонней непрерывности.

В определении непрерывности функции в точке х0 требуется существование 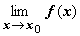и равенство 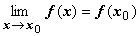. С применением односторонних пределов определяются понятия непрерывности функции в точке слева и справа:

Опр.. Функция f(x) называется непрерывной в точке х0 слева, если .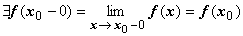

Опр. Функция f(x) называется непрерывной в точке х0 справа, если .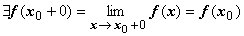

Опр. Если одно из этих условий не выполнено, то функция f(x) имеет в точке х0 разрыв, соответственно, слева или справа.

Если функция определена на отрезке [a,b], то в левом конце отрезка х0= a можно говорить только о непрерывности справа, в правом конце (х0= b) - о непрерывности слева. Для внутренней точки отрезка функция f(x) непрерывна в точке х0 тогда и только тогда, когда она непрерывна в этой точке слева и справа

2) Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).

При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.

3) Теорема Больцано — Коши

Пусть дана непрерывная функция на отрезке 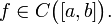Пусть также 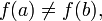и без ограничения общности предположим, что 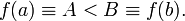Тогда для любого 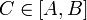существует 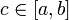такое, что