Инверсный код с повторением

В основу построения кода положен метод повторения исходной кодовой комбинации. Однако в зависимости от четного или нечетного числа единиц в исходной комбинации последняя передается в неизменном виде, либо в инвертированном виде.

Пример.

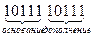- четное число единиц.

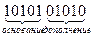- нечетное число единиц.

Декодирование производится следующим образом. Сначала суммируются все «1» первой комбинации из 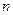разрядов. Если их оказалось четное число, то вторые «п» разрядов без изменения сравниваются поразрядно с первыми. Если число «1» в первой комбинации нечетные, повтор ее инвертируется, а затем уже сравнивается. Если имеется хотя бы одно несовпадение, все 2п элемента стираются (приема нет, ошибки обнаружены).

При использовании этого кода ошибка не будет обнаружена, если одновременно исказятся два (четыре, шесть) элемента в исходной комбинации и элементы с теми же порядковыми номерами в повторной комбинации. Вероятность такого искажения зависит от распределения ошибок в канале, по которому ведется передача.

Защита от групповых ошибок в данном случае зависит еще и от длины кодовых комбинаций п.

Предположим, что все 2п разрядов поражены групповой ошибкой с 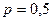. Примем или не примем эту кодовую комбинацию, определится соответствием повторов. Если из-за помех в первых 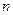разрядах оказалась какая-то комбинация непохожая на переданную, то она будет принята как правильная, если в последующих « 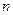» разрядах окажется она же (или инверсная комбинация). Вероятность такого события ~ равна 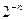, при .

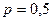Если 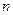мало, то условная вероятность ложного приема при групповой ошибке велика, если 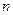велико, 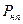- мала.

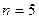
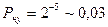Так при , при .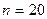

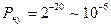Код Хэмминга

Код Хэмминга относится к линейным систематическим корректирующим кодам с проверкой на четность. Этот код строится путем добавления к « 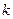» информационным символам, образующим кодовую комбинацию, 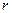проверочных символов. Проверочные элементы получаются по результатам проверки на четность групп символов. Так, если к последовательности двоичных символов 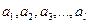добавляется двоичный символ 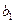так, что последовательность содержит четное число единиц, то говорят: 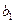- определяется проверкой на четность.

В основу построения кода Хэмминга положены следующие правила:

При кодировании к 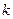информационным двоичным символам путем 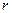проверок на четность добавляется 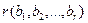проверочных двоичных символов (во всей группе, включая проверочный, число единиц всегда четно, каждая проверка охватывает определенную группу символов).

При декодировании проверяются на четность те же группы. Если число единиц в группе четно, то результат проверки - 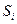принимается равным «0», в противном случае – «1» (произошла ошибка). Если 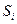проверка дала в результате «1», то это означает, что исказился один из символов, входящий в 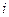-ю группу.

Проверочные группы выбираются так, чтобы, записав результаты проверок 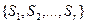в виде двоичного числа 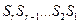получился номер искаженного элемента.

Это требование позволяет определить число необходимых проверочных разрядов. Число элементов в коде - 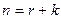, число разрядов двоичного числа, которое указывает номер искаженного элемента - 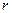, следовательно, 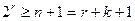; 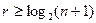. Иначе, при передаче может быть искажен любой символ (п) или искажений нет (1) – столько вариантов надо различать с помощью проверок.

;

; .

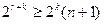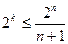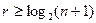Найдем правило, согласно которому определяется состав проверочных групп. Мы потребовали, чтобы число 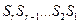указывало двоичный номер искаженного символа. «1» в 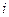-ом разряде этого числа указывает на то, что исказился символ, двоичный номер которого содержит «1» в 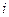-ом разряде. Значит, проверка, в результате которой получается 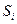, должна охватывать все символы, порядковые двоичные номера которых содержат «1» в 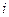-ом разряде.

Удобно, чтобы проверочный элемент, при этом, входил только в одну из групп проверок. В противном случае получится дополнительная неопределенность.

Таким образом, контролирует разряды 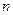-разрядного числа 1, 3, 5, 7, 9,…

: 2, 3; 6, 7; 10, 11; 14, 15

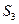: 4, 5, 6, 7, 12, 13, 14, 15,…

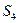: 8, 9, 10, 11, 12, 13, 14, 15; и т.д.

Элементы, входящие в каждую из проверочных групп только один раз, имеют номера 1, 2, 4, 8, 16, 32 и т.д. их мы и выбираем в качестве контрольных.

Процедуру кодирования – декодирования кодом Хэмминга проиллюстрируем примером.

Пусть 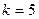. Тогда, согласно 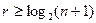; 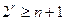, 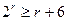получим .

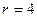двоичные символы	а1	а2	а3	а4	а5	а6	а7	а8	а9
итог кодирования					0_

Пусть хотим передать сообщение 10101. Записываем его в позициях информационных разрядов: .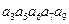

Находим значения контрольных символов.

1.

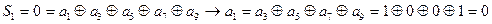
2.

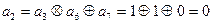
3.

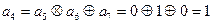
4.

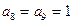
Получим: 001101011

Пусть в канале при передаче исказился седьмой символ и принято сообщение 001101111.

Определим номер искаженного символа и декодируем сообщение.

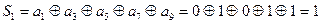
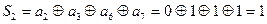
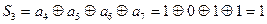
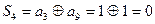
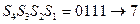
Определили номер искаженного символа и инвертируем его (символ), т.е. передавалось: 10101.

Если получим 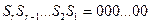, это говорит об отсутствии ошибок. Если точнее на отсутствие одиночных ошибок; с двойными, тройными и более высокой кратности ошибками этот код бороться не может.