Интеграл от разрывной функции

Пусть функция f (x) непрерывна в интервале [a,b), но имеет разрыв в точке x = b. В этом случаенесобственный интеграл определяется в виде

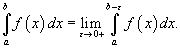
Аналогично можно рассмотреть случай, когда функция f (x) непрерывна в интервале (a,b], но имеет разрыв при x = a. Тогда

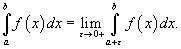
Если приведенные выше пределы существуют и конечны, то говорят, что соответствующие несобственные интегралы сходятся. В противном случае они считаются расходящимися.

Пусть f (x) непрерывна для всех действительных x в интервале [a,b], за исключением некоторой точки 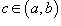. Тогда справедливо соотношение

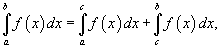
и говорят, что несобственный интеграл 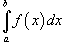сходится, если оба интеграла в правой части верхнего равенства сходятся. В противном случае несобственный интеграл расходится.

10. Геометрические приложения определенных интегралов.