Интеграл от функции комплексной переменной.

ГЛАВА 2. ИНТЕГРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ АНАЛИТИЧЕСКИХ ФУНКЦИЙ

Интеграл от функции комплексной переменной.

Определение и условие существования. Пусть на комплексной плоскости задана произвольная ориентированная кривая L. Пусть в каждой точке этой кривой определена функция комплексной переменной f(z). Рассмотрим разбиение кривой L на дуги 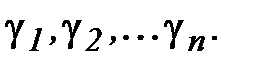набором точек z₀ ,z₁,…z_n. Числа 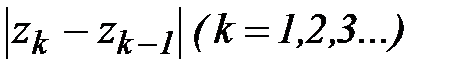есть длины хорд, соединяющие соседние точки, ограничивающие дуги 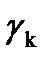и на каждой дуге возьмем точку 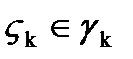, в которой вычислим значение функции.

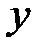
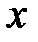
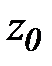
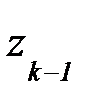
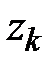
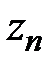
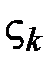
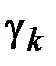
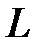
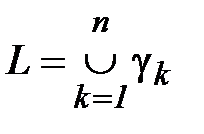
Рис.1.

Составим следующую интегральную сумму: 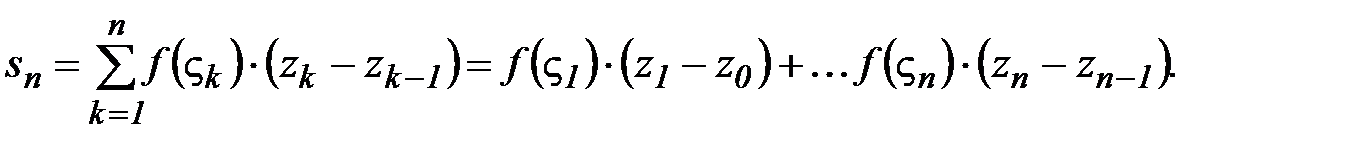(1)

Определение 1.Интегралом от функции комплексной переменной f(z)по ориентированной кривой L называется предел интегральных сумм (1) при 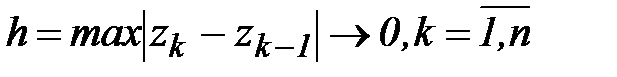, если он существует независимо от способа разбиения кривой L набором точек z_kи выбора точек 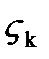на дугах 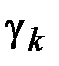, что записывается в виде:

.

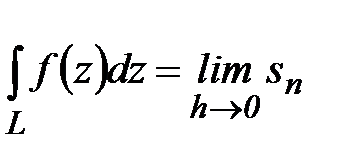Пример 1.Вычислить интеграл 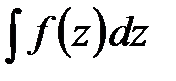, где подинтегральная функция тождественно равна единице, а L-кривая, соединяющая две произвольные точки z=aи z=bна комплексной плоскости (рис.2).

Решение.

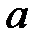
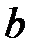
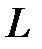
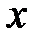
Рис.2.

.

.

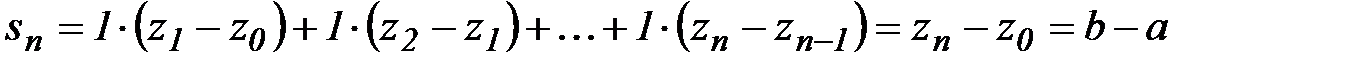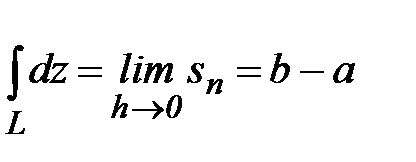Таким образом, рассмотренный интеграл зависит только от начальной и конечной точки интегрирования и не зависит от кривой, соединяющей эти точки.

Теорема 1.Интеграл от функции комплексной переменной по кривой L существует, если кривая L кусочно-гладкая, а функция f(z) непрерывна на ней.

□ Рассмотрим снова некоторое разбиение кривой точками z₀ ,z₁,…z_n.

Обозначим

.

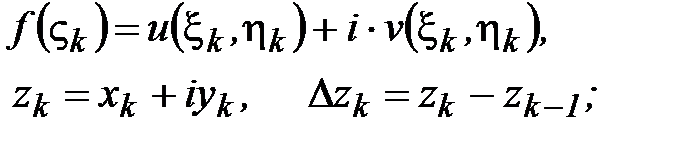
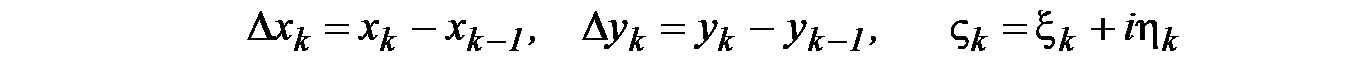Составим n-ю частичную сумму: .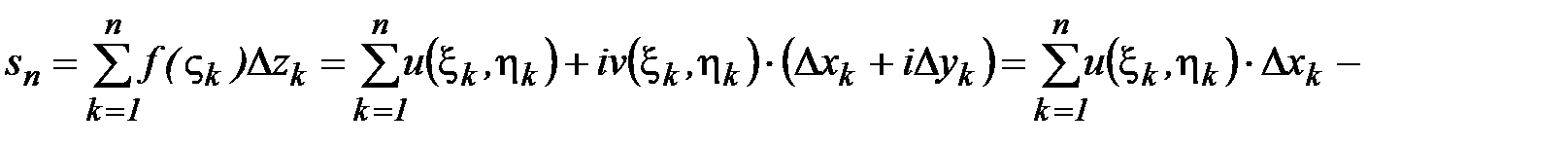

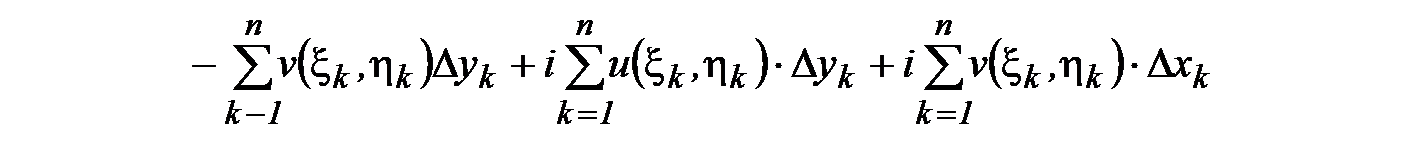Поскольку функция f(z) непрерывна на кривой, то непрерывными будут её действительная и мнимая части, т.е. функции 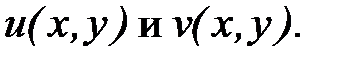Тогда, если перейти к пределу при 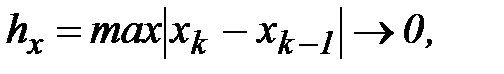то первое слагаемое 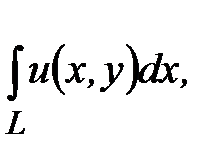будет криволинейным интегралом второго рода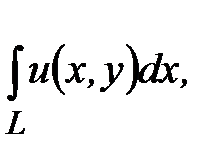

Аналогично для всех остальных слагаемых получим, что они при предельном переходе будут равны соответствующим криволинейным интегралам второго рода с учетом, что 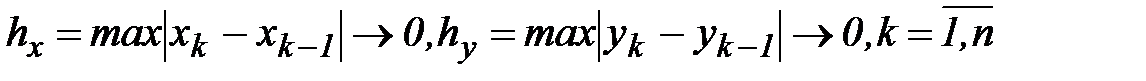. В итоге из n-ой частичной суммы функции комплексной переменной получим в результате предельного перехода равенство:

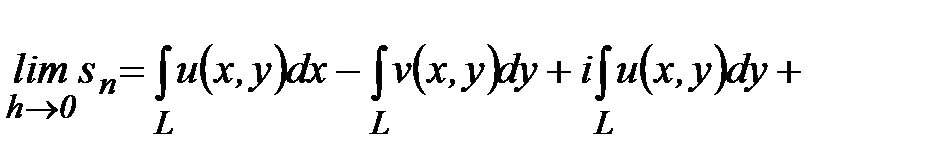
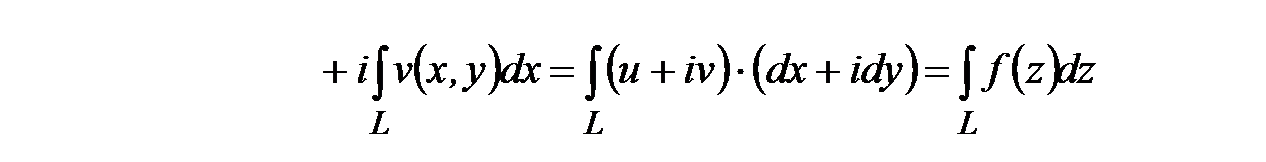(2)

Последний переход в этом равенстве обусловлен свойством линейности криволинейных интегралов и свойствами комплексных чисел. Таким образом, при выполнении условий теоремы существует 4 криволинейных интеграла функций действительной переменной в правой части равенства (2) и, следовательно, существует интеграл функции комплексной переменной. Формула (2) позволяет вычислять интеграл функции комплексной переменной через криволинейные интегралы второго рода.

Пример 2.Вычислить интеграл 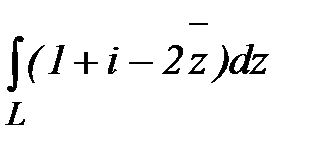по линиям: а) прямая; б) парабола y=x², соединяющим точки z₁=0 и z₂=1+I.

На практике для вычисления интегралов часто используется показательная форма комплексных чисел.

Пример 3.Вычислить 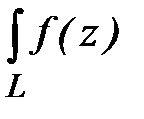, если L: .

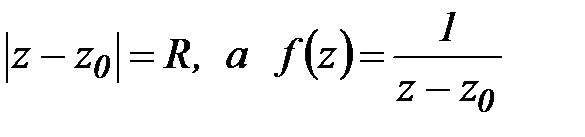Решение.

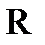
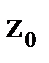
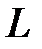
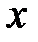
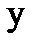
Рис.3.

Сделаем замену переменной, т.е. запишем в показательной форме, обозначив 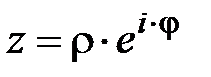. Для точек, лежащих на окружности, будем иметь: 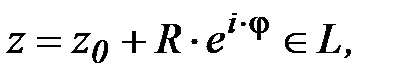0<φ<2π, .

.

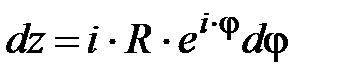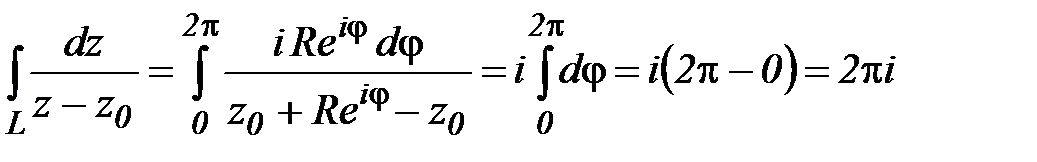Свойства.Пусть функции f(z)и g(z) непрерывны на кусочно-гладкой ориентируемой кривой L. Тогда справедливы следующие свойства.

Линейность: 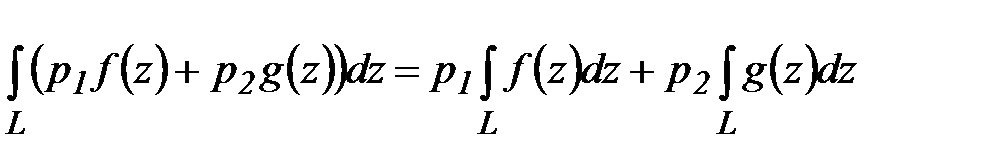, где 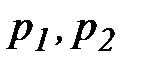- произвольные комплексные числа.

Ориентированность: .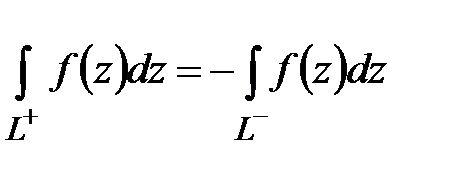

Аддитивность:Пусть 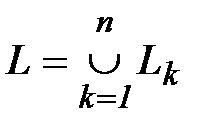, тогда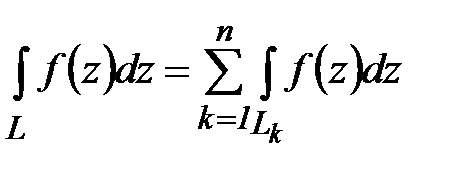

Оценка интеграла: 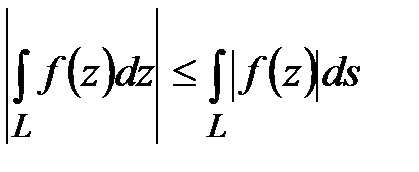,где 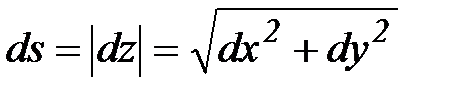, ds- дифференциал дуги кривой L.

Формула замены переменной: 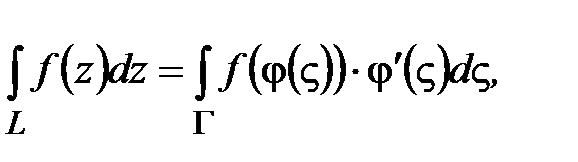где 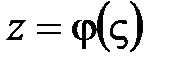- аналитическая функция, устанавливающая взаимно-однозначное соответствие между кривыми L и Г.

Справедливость указанных свойств следует из формулы (2) и соответствующих свойств криволинейных интегралов.