Тензоры

И ЭЛЕМЕНТЫ ТЕОРИИ НАПРЯЖЕНИЙ

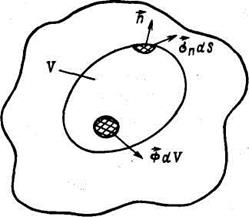Для изучения движения сплошной среды в связи с причинами, которые это движение вызывают, вводят понятие о силах. Силы могут быть внешними и внутренними. Первые являются следствием воздействия на рассматриваемое тело других тел, а вторые возникают в результате взаимодействия элементов данного тела. Внешние и внутренние силы могут быть двоякого рода: объемные (или массовые) и поверхностные. Объемная сила действует на массу, заключенную в произвольном элементе объема тела, например сила тяжести.

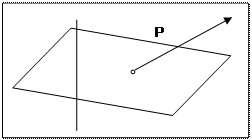
Рис. 4. Схема действия массовых и поверхностных сил в объеме V

Пусть 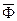(x,t)— объемная сила, отнесенная к единице объема. Тогда сила, действующая на бесконечно малый объем dV, равна

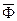dV, а на объем V—равна dV (рис. 1).

Поверхностная сила действует на элементы, которые можно мысленно выделить внутри тела или на его поверхности.

Сила, действующая на бесконечно малый элемент поверхности dS, равна 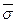dS, где 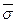— вектор силы, рассчитанный на единицу площади элемента и приложенный в любой его точке, называется вектором напряжения или просто напряжением (см. рис. 1).

Напряжение 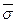зависит от положения элемента dS, т. е. от ориентировки его

в теле. Если требуется указать, что напряжение 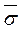относится к площадке с нормалью п, то пишут .

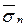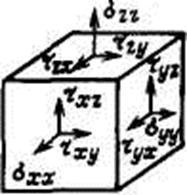
Проекции этого вектора на оси произвольной системы координат Ох₁х₂х₃ обозначаются через σ_nj (j=1, 2, 3). В частности, проекции напряжений 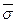_xi, отнесенные к площадкам, перпендикулярным к координатным осям Ox_i, обозначаются через σ_ij (i,j = 1,2,3), где σ_ii называются нормальными напряжениями, а σ_ij = σ_ji (i≠j) — касательными напряжениями, действующими на этих площадках (рис. 5). Легко доказать следующие очень важные соотношения:

σ_nj = 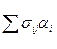( i, j = 1,2,3), (1.29)

которые позволяют найти компоненты вектора напряжения для произвольной площадки с нормалью 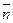, проходящей через точку М; α_i = cos(n, х_i) (i = 1, 2, 3).

Поэтому говорят, что совокупность шести величин σ_ij, называемых компонентами симметричного тензора напряжений, полностью характеризует напряженное состояние в точке тела М.

Рис. 5. Расположение компонент тензора напряжений относительно выбранной декартовой системы координат

Рис. 6. Векторы напряжений в точке М, действующие в двух произвольно ориентированных площадках

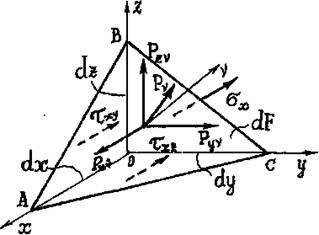
Рис. 7. Нормальная и касательная проекции вектора напряжения

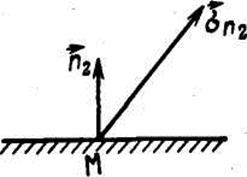
Пусть заданы две площадки, проходящие через одну и ту же точку М (рис. 6). Используя формулу (1.29), нетрудно доказать, что проекция напряжения 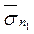, действующего на первую площадку, на нормаль 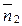ко второй равна проекции напряжения 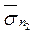, действующего на вторую площадку, на нормаль 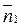к первой и вычисляется по формуле

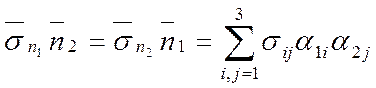
(1.30)

где α_1i и α_2j — направляющие косинусы нормале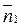й и 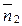. Эта формула позволяет вычислить проекцию на любое направление вектора напряжения, действующего на данную площадку. В частности, проектируя вектор 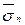на направление нормали, получаем нормальное напряжение (рис. 7)

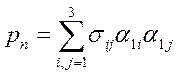(1.31)

Касательное напряжение на этой же площадке равно

(1.32)

где σ_n — величина вектора напряжения .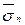

Из формулы (1.30) следуют формулы перехода от одной системы Ох₁х₂х₃ координат к другой О ;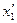

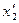
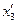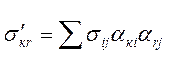(1.33)

где σ'_кr — компоненты тензора напряжений относительно новой системы координат;

α_кi = cos( 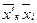), α_rj = cos( ).

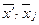Например, зависимость между напряжениями в декартовой (Ох₁х₂х₃) и цилиндрической (r, θ, z) системах координат с общей осью Ox₃ = Oz имеет вид

σ_rr = σ₁₁cos²θ + σ₂₂ sin²θ + σ₁₂ sin 2θ;

σ_θθ= σ₁₁ sin²θ + σ₂₂ cos²θ - σ₁₂ sin 2θ;

σ_zz = σ₃₃; (1.34)

σ_rθ = 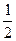( σ₂₂ - σ₁₁)sin 2θ + σ₁₂ cos2θ;

σ_rz = σ₁₃ cosθ + σ₂₃sin θ;

σ_θz= - σ₁₃ sinθ + σ₂₃ cosθ;

где σ_rr—радиальное напряжение, действующее на площадке, перпендикулярной к радиусу; σ_θθ — тангенциальное (окружное) напряжение, действующее на площадке, нормаль которой перпендикулярна к радиусу.

Принимая во внимание известные соотношения аналитической геометрии

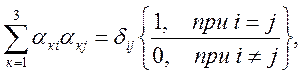
из формул (1.33) после суммирования левой и правой частей по к (при r = к) получается важное соотношение

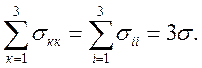(1.35)

Оно показывает, что величина σ, называемая средним нормальным напряжением, инвариантна по отношению к преобразованию системы координат.

Характерной особенностью напряженного состояния сплошной среды является наличие в каждой точке тела, по крайней мере, трех взаимно перпендикулярных площадок, на которых касательные напряжения σ_ij (i≠j) равны нулю. Направления нормалей к этим площадкам образуют главные направления, которые не зависят от исходной системы координат. Соответствующие напряжения σ_ii=σ_i называются главными нормальными напряжениями. Поэтому любое напряженное состояние в рассматриваемой точке может быть вызвано растяжением (сжатием) окрестности точки в трех взаимно перпендикулярных направлениях.

Главные нормальные напряжения могут быть найдены из следующего кубического уравнения:

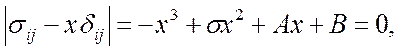
корни этого уравнения могут быть только вещественными.

Так как решения этого уравнения х_i = σ_i (i=1,2,3) не зависят от выбора системы координат, коэффициенты σ, А, В также не должны зависеть, т. е. они инвариантны. Это еще одно доказательство инвариантности среднего напряжения

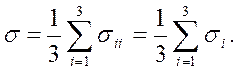(1.36)

Два других инварианта физического смысла не имеют.

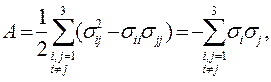
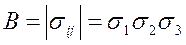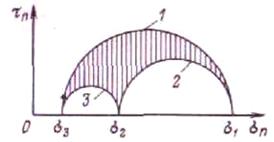
(1.37)

Рис. 8. Диаграмма Мора:

/, 2, 3 — окружности, координаты которых определяют нормальные и касательные напряжения на площадках, проходящих через главные оси 1, 2, 3 соответственно

Если главные направления совпадают с координатными осями (Ох_i), то формулы (1.31) — (1.34) упрощаются. Например, формулы (1.31) и (1.32) принимают вид

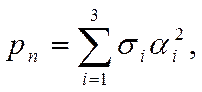(1.38)

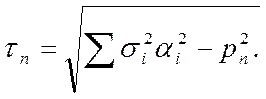
где α_i= cos (n, x_i).

Отсюда нетрудно получить, что напряжения р_п и τ_n могут лежать только внутри области, заштрихованной на рис.8. Это так называемая диаграмма Мора, дающая наглядное представление о напряжениях в различных сечениях, проходящих через данную точку. Здесь принята нумерация главных осей такой, чтобы выполнялись условия

σ₁ ≥ σ₂ ≥ σ₃ (1.39)

Практический интерес представляют сечения, проходящие через главные оси. На рис. 8 точкам какой-либо окружности 1, 2 или 3 отвечают площадки, содержащие соответствующую главную ось.

Если площадка содержит главную ось Ox₁ и наклонена под углом θ к оси Ох₂, то из формул (1.38) получается

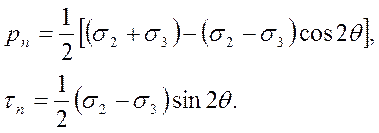
Эти напряжения соответствуют координатам точек окружности № 1 (см. рис. 8).

По аналогии можно записать формулы для напряжений, действующих на площадках, проходящих через две другие главные оси, иначе, для координат точек окружностей № 2 и 3 на рис. 8.

При θ = π/4, т. е. в сечениях, делящих пополам углы между главными плоскостями, касательные напряжения принимают экстремальные значения

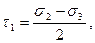
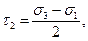
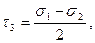
называемые главными касательными напряжениями,

а нормальные напряжения равны полусуммам

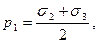
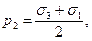
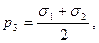
что соответствует координатам центров окружностей 1, 2 и 3 (см. рис. 8). Наибольшее из значений τ_i (i = 1, 2, 3) называется максимальным касательным напряжением и обозначается τ_max. Если условия (1.39) выполняются, то τ_max = τ₂.

Так как различные тела обладают различными механическими свойствами по отношению к сдвигу и равномерному всестороннему сжатию, удобно компоненты тензора напряжения представить в виде суммы

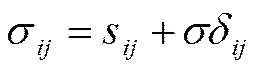
где S_ij—компоненты тензора, характеризующего касательные напряжения в данной точке и называемого девиатором напряжений.

Нормальные составляющие девиатора обозначают S_ii = σ_ii — σ, а касательные составляющие s_ij = σ_ij (i≠j).

Главные направления девиатора напряжений (S_ij) и тензора напряжений (σ_ij) совпадают, а главные значения s_i отличаются от σ_i, на величину среднего (гидростатического) давления и определяются кубическим уравнением

-s³ + A₁s+B₁=0,

все корни которого также вещественны.

Инварианты A₁ и В₁ легко получить из формул (1.37), если заменить σ_ij на s_ij и σ_i на s_i.

Неотрицательную величину

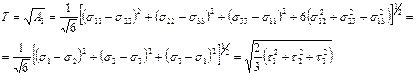
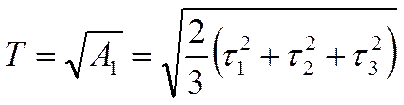(1.40)

называют интенсивностью касательных напряжений.

Часто рассматривают приведенное напряжение или интенсивность напряжений

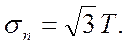(1.41)

Величина Т равна нулю только в том случае, когда напряженное состояние есть состояние гидростатического давления.

Доказывается, что с погрешностью не более 7% имеет место равенство

Т ≈ 1,08 τ_max.

Для характеристики вида напряженного состояния, подобно характеристике деформационного состояния, используется параметр, введенный Лоде и Надаи:

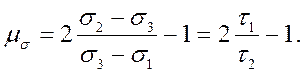
который изменяется в пределах от —1 до +1. Он указывает на взаимоотношение главных нормальных напряжений, в частности на положение точки σ₂ на диаграмме Мора. Для одних и тех же величин μ_σ диаграммы Мора подобны.

Для чистого растяжения элемента (σ₁>0, σ₂= σ₃ = 0) μ_σ= —1, для чистого сжатия (σ₁ = σ₂ = 0, σ₃<0) μ_σ= 1, для сдвига (σ₁>0, σ₂=0, σ₃= — σ₁) μ_σ= 0, для гидростатического давления (σ₁ = σ₂ = σ₃) μ_σ не имеет смысла.

§ 4. Источник и сток в пространстве.

Рассмотрим еще один важный для дальнейшего пример потенциального течения. Пусть

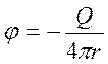(1.42)

где 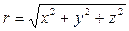, a Q = const или Q = Q (t). Ясно, что поверхностями равного потенциала j = const являются в этом случае поверхности r = const, т. е. концентрические сферы с центром в начале координат. Скорость v = grad j ортогональна к этим сферам, т. е. направлена по радиусам. Линии тока являются лучами, выходящими из начала координат.

Пусть Q > 0; тогда, так как grad j направлен в сторону роста j, то v направлена по r. Если Q < 0, то v направлена по - r (рис. 6). Величина скорости равна:

|(grad j_r)| = .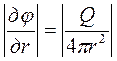

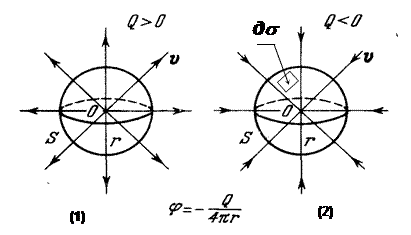Рис. 6

Скорость стремится к нулю при r ® ¥ и к бесконечности при r ® 0. Точки нуль и бесконечность являются критическими. При Q > 0 (1) имеем

вытекание жидкости из начала координат во всех направлениях — это течение называется точечным пространственным источником. При Q < 0 (2) — втекание жидкости в начало координат — сток. В первом случае в бесконечно удаленной точке имеем источник, а во втором — сток.

Вычислим объем жидкости, протекающей за единицу времени через поверхность сферы S некоторого радиуса r с центром в начале координат. Через элемент сферы ds за единицу времени протекает объем жидкости v ds, а через всю сферу

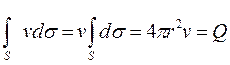(расход жидкости)

( v можно вынести за знак интеграла, так как v = const на поверхности сферы). Заметим, что первые два равенства верны всегда, когда v = v (r) и v ортогональна к поверхности сферы S. Вычисленный объем жидкости не зависит от r. Таким образом, несмотря на то, что на разных сферах разного радиуса с центром в начале координат скорости разные, постоянная Q в потенциале j (1.42) является объемом жидкости протекающей за единицу времени через каждую такую сферу. Величина Q называется расходом или мощностью источника (стока).

Если Q = const, то источник или сток имеет постоянную мощность; если Q = Q (t) — то переменную. Если в некоторый момент времени Q меняется в начале координат, то мгновенно измеряется поле скоростей во всем пространстве. Сигналы изменение Q сразу сказываются на всем поле скоростей, что, конечно, не может иметь места в действительности. Возмущения должны распространяться с некоторой конечной скоростью. Поэтому рассмотренное поле скоростей является определенной идеализацией, которая может достаточно хорошо отражать действительность только в том случае, когда рассматриваются течения жидкости с большой скоростью распространения возмущений. Во многих случаях можно считать, что такой жидкостью является, например, вода, в которой скорость распространения слабых возмущений 1450 м/сек.

Греческий алфавит

Α α – альфа Ν ν – ни (ню)

Β β – бэта Ξ ξ – кси

Γ γ – гамма Ο ο – омикрон

Δ δ – дельта Π π – пи

Ε ε – эпсилон Ρ ρ – ро

Ζ ζ – дзэза Σ σ – сигма

Η η – эта Τ τ – тау

Θ θ – тэта Υ υ – ипсилон

Ι ι – иота Φ φ – фи

Κ κ – каппа Χ χ – хи

Λ λ – ламбда Ψ ψ – пси

Μ μ – ми (мю) Ω ω – омега

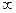
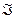
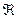
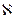
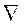- набла (от греч.-ναβλα - арфа) – знак действия над полем (оператор) –

этот оператор Гамильтона векторно-дифференциальный

¢

£

¤

¥

¿

ñ

æ

ě

ę

Ģ

į

Ķ

Ł

ł

Œ

œ

ə

ΐ

‰

₤

₧

₪

₫

€

℅

™

ТЕНЗОРЫ

Понятие тензора (от латинского tendo — напрягаю, растягиваю) принадлежит к числу основных, фундаментальных математических понятий и широко применяется сейчас в механике, электродинамике, теории относительности и т. д. Первоначально возникшее в рабо­тах XIX века по теории упругости, оно было систематически иссле­довано в 1886 —1901 гг. итальянским геометром Г. Рйччи-Курбастро (1853—1925) и итальянским математиком и механиком Т. Лёви-Чивйта (1873—1942).

Внимание к новому аппарату существенно возросло после создания в 1915 —1916 гг. великим ученым, физиком А. Эйнштейном (1879 — 1955) общей теории относительности, мате­матическая часть которой целиком основана на тензорном исчислении. Физические величины, которые нам встре­чались до сих пор, были либо скалярными, либо векторными. Однако существуют физические величины более сложной природы.

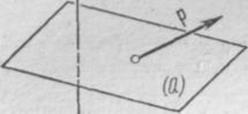
Например, однородное напряженное состоя­ние упругого тела характеризуется плотностью р силы, с которой одна часть тела действует на другую через мысленно вы­деленную плоскость (Q) (рис. 1); однако при этом р для различных направлений плоскости (Q) будет различным. Таким образом, вели­чина, характеризующая напряженное состояние, уже не является вектором, она представляет собой тензор 2-го ранга. Оказывается, что и многие другие важные величины, характеризующие состояние сплошных сред, также являются тен­зорами.

К настоящему времени тензорная алгебра, а также тензорный анализ (т. е. теория тензорных полей, связанная с применением диф­ференцирования и интегрирования) представляют собой значительно разработанные дисциплины.

§ 1. Тензорная алгебра

1. Примеры.К понятию тензора можно прийти уже размышляя над описанием векторов в обычном пространстве с помощью чисел. Как известно из векторной алгебры, все действия над векторами удобно осуществлять, выбрав евклидов базис i, j, k, после чего можно любой вектор а разложить по этому базису

а = а_хi + а_уj+ a_zk (1)

и взамен действий над векторами осуществлять действия над их про­екциями, т. е. над числами — коэффициентами разложений. Более того, даже задавать конкретные векторы обычно бывает удобнее с помощью разложения (1), чем каким-то геометрическим способом.

Однако задумаемся теперь, что это за векторы i, j, k. В некото­рых случаях, когда в задаче имеется естественная система отсчета направлений (например, во многих задачах статики), эти векторы можно описать вполне точно, «привязав» их к данным задачи. Но во многих случаях привлечение такой «абсолютной» системы отсчета является весьма искусственным либо вообще невозможно. Тогда по­лучается на первый взгляд парадокс: мы пользуемся проекциями вполне определенного вектора, которые зависят от выбора базиса, но не уточняем, как этот базис выбирается...

Эта трудность будет преодолена, если с самого начала отка­заться от выбора какого-то одного базиса, а считать, что все ба­зисы равноправны и каждому выбору базиса i, j, k отвечает на­бор значений а_х, а_у, а_z в соответствии с формулой (1). Подобный набор величин, приобретающих определенные значения лишь после выбора базиса и преобразующихся по определенному правилу при за­мене базиса (см. ниже), и называется тензором (или тензорной вели­чиной), а сами эти величины, составляющие в определенном порядке тензор, называются его компонентами. (Отметим некоторое несо­ответствие: в векторной алгебре принято компонентами вектора A называть в е к торы а_хi, а_уj, a_zk. Однако здесь мы будем компонентами называть величины а_х, а_y , а_z.)

В тензорном исчислении принято не писать знак суммы по повто­ряющемуся индексу, а при повторении индекса всегда осуществлять такое суммирование, т. е. писать последнюю формулу.

Здесь индекс суммирования является немым и может быть обозна­чен любой буквой, а пределы суммирования определяются размер­ностью пространства, в котором рассматривается тензор.

Напряженное состояние в окрестности точки

Если через произвольную точку тела провести три взаимно перпендикулярные площадки параллельно координат­ным плоскостям, то девять составляющих (компонент) напря­жения: три нормальных а_х, а_у, ст_г и шесть касательных х_ху, т,₂, т_2Х, т_ух, t_xz, х_zy, действующих на этих площадках (рис. 4.1),

полностью определяют напряженное состояние в окрестности данной точки. Это означает, что, зная эти девять величин, можно найти напряжения на любой наклонной площадке, проходя­щей через данную точку. Слово «со­ставляющая» или «компонента» в дальнейшем для краткости будем опускать.

Все девять напряжений можно обозначить одинаково, например, Gij{hj=x, У, z). Тогда при г'=у получа­ются нормальные напряжения, в которых сохраняется только один индекс, а при i Ф]—касательные напряжения. Первый индекс указывает, параллельно какой оси направлено напряже­ние, а второй обозначает нормаль к площадке, на которой оно действует. Это правило непосредственно относится к касатель­ным напряжениям, но им также можно пользоваться и для нормальных напряжений, если употреблять обозначения <у_и.

Нормальные напряжения считаются положительными, если они направлены в сторону внешней Нормали к площадке, и наоборот. В соответствии с этим правилом положительные нормальные напряжения считаются растягивающими, а от­рицательные — сжимающими.

Для касательных напряжений принимается следующее правило знаков. На площадке, внешняя нормаль к которой направленав положительном (или отрица­тельном) направлении соответст­вующей оси, касательное напряже­ние считается положительным, ес­ли оно также направлено в поло­жительном (или отрицательном) направлении оси. На рис. 4.1 пока­заны положительные напряжения.

Проведем вблизи точки О тела произвольную наклонную площад­ку ABC, площадь которой обозна­чим через dF(рис. 4.2). Положение этой площадки может быть опреде­лено углами, которые составляет нормаль v с осями координат.

Как известно из аналитической геометрии, направляющие косинусы нормали связаны между собой соотношением

l² + m²+n² = 1. (4.1)

Полное напряжение p_v, действующее на этой площадке, можно спроектировать на оси координат. Проекции p_xv, p_yv, p_zv определяются из уравнений равновесия тетраэдра ОАВС. Составим сумму проекций всех сил, приложенных к граням тетраэдра, на ось Ох (на рис. 4.2 на вертикальных и горизон­тальной гранях тетраэдра показаны только те напряжения, которые дают проекции на ось