Линейная зависимость и независимость векторов
ЛИНЕЙНЫЕ, ЕВКЛИДОВЫ И УНИТАРНЫЕ ПРОСТРАНСТВА
Линейные пространства
Определение. Множество векторов  называется вещественным линейным пространством, если в этом множестве введены операции сложения двух векторов (т.е. каждой паре
называется вещественным линейным пространством, если в этом множестве введены операции сложения двух векторов (т.е. каждой паре 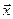 ,
, 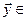
 поставлен в соответствие определенный элемент
поставлен в соответствие определенный элемент 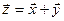 из множества
из множества  ) и умножения вектора на вещественное число (т.е. каждому вектору
) и умножения вектора на вещественное число (т.е. каждому вектору 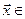
 и произвольному числу
и произвольному числу 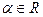 поставлен в соответствие определенный элемент
поставлен в соответствие определенный элемент  из множества
из множества  ), и эти две операции удовлетворяют следующим аксиомам:
), и эти две операции удовлетворяют следующим аксиомам:
1) 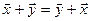 для
для 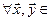
 ;
;
2) 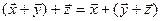 для
для 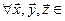
 ;
;
3) во множестве  существует нулевой вектор
существует нулевой вектор 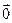 такой, что
такой, что 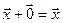 для
для 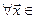
 ;
;
4) для 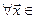
 вомножестве
вомножестве  существует противоположный вектор
существует противоположный вектор 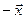 такой, что
такой, что 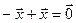 ;
;
5) для 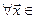
 выполняется
выполняется 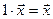 ;
;
6) для 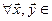
 и
и 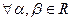 выполняются равенства
выполняются равенства
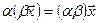 ;
;
 ;
;
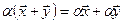 .
.
Определение. Арифметическим пространством Rnназывается множество векторов 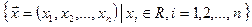 , в котором операции сложения векторов и умножения вектора на число определены следующим образом: если
, в котором операции сложения векторов и умножения вектора на число определены следующим образом: если 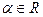 ,
, 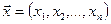 ,
, 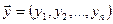 , то
, то
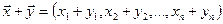 ,
, 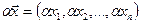 .
.
Утверждение. Множество всех решений однородной системы образует
линейное пространство.
Определение. Линейной комбинацией векторов 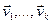 называется сумма вида
называется сумма вида 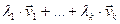 , где
, где 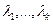 - произвольные числа.
- произвольные числа.
Утверждение. Множество всех линейных комбинаций векторов 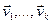 образует линейное пространство.
образует линейное пространство.
Задачи
3.1. Доказать, что следующее множество является линейным пространством, указать его нулевой элемент, а также какой-либо конкретный элемент этого пространства и противоположный ему элемент:
а) множество решений однородной системы 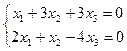 ;
;
б) множество решений однородной системы 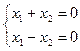 ;
;
в) множество всех квадратных матриц n-го порядка;
г) множество всех симметричных матриц n-го порядка;
д) множество всех векторов, лежащих на одной оси;
е) множество всех линейных комбинаций векторов 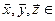 R3.
R3.
3.2. Доказать, что множество всех решений однородной системы образует линейное пространство.
3.3. Доказать, что множество всех линейных комбинаций векторов 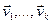 образует линейное пространство.
образует линейное пространство.
3.4. Является ли линейным пространством множество
а) всех решений неоднородной совместной системы линейных уравнений;
б) всех векторов координатной плоскости, каждый из которых лежит на одной из координатных осей;
в) всех многочленов степени не выше n;
г) всех многочленов n-ой степени;
д) всех сходящихся числовых последовательностей;
е) всех числовых последовательностей 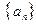 , сходящихся к даному числу
, сходящихся к даному числу 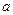 .
.
3.5. Доказать, что
а) множество всех непрерывных функций, заданных на отрезке 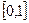 , где сумма произвольных функций
, где сумма произвольных функций  и
и 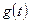 вычисляется как
вычисляется как 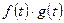 , а произведение функции на число вычисляется обычным образом, не является линейным пространством;
, а произведение функции на число вычисляется обычным образом, не является линейным пространством;
б) множество всех векторов пространства R3, где сумма произвольных векторов  и
и 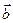 вычисляется как
вычисляется как 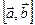 , а произведение вектора на число вычисляется обычным образом, не является линейным пространством;
, а произведение вектора на число вычисляется обычным образом, не является линейным пространством;
в) множество всех диагональных матриц n-го порядка, где сумма произвольных матриц 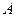 и
и 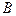 вычисляется как
вычисляется как 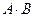 , а произведение матрицы на число вычисляется обычным образом, не является линейным пространством;
, а произведение матрицы на число вычисляется обычным образом, не является линейным пространством;
г) множество всех вещественных чисел, в котором сумма произвольных чисел 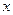 и
и 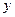 вычисляется как
вычисляется как 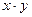 , а произведение числа на число вычисляется обычным образом, не является линейным пространством.
, а произведение числа на число вычисляется обычным образом, не является линейным пространством.
3.6. Доказать, что
а) множество всех положительных чисел, в котором сумма произвольных чисел 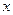 и
и 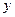 вычисляется как
вычисляется как 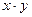 , а произведение вещественного числа
, а произведение вещественного числа 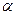 на произвольное положительное число
на произвольное положительное число 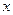 вычисляется как
вычисляется как 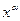 , является линейным пространством;
, является линейным пространством;
б) множество всех положительных функций, заданных на множестве 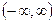 , если сумма произвольных функций
, если сумма произвольных функций 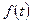 и
и 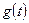 вычисляется как
вычисляется как 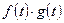 , а произведение функции
, а произведение функции 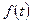 на число
на число 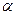 вычисляется как
вычисляется как 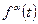 , является линейным пространством.
, является линейным пространством.
Линейная зависимость и независимость векторов
Определение. Система векторов 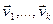 называется линейно независимой, если равенство
называется линейно независимой, если равенство 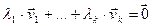 выполняется только при
выполняется только при 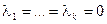 .
.
Утверждение. Система векторов линейно независима тогда и только тогда, когда ни один из этих векторов не является линейной комбинацией остальных векторов данной системы.
Определение. Система векторов 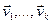 называется линейно зависимой, если существуют числа
называется линейно зависимой, если существуют числа 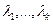 , не равные нулю одновременно, при которых выполняется равенство
, не равные нулю одновременно, при которых выполняется равенство  .
.
Утверждение. Система векторов 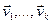 линейно зависима тогда и только тогда, когда хотя бы один из этих векторов является линейной комбинацией остальных векторов данной системы.
линейно зависима тогда и только тогда, когда хотя бы один из этих векторов является линейной комбинацией остальных векторов данной системы.
Примеры
1. Являются ли линейно зависимыми (независимыми) векторы
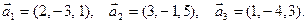
Решение. По определению линейная зависимость или независимость векторов устанавливается исходя из условия равенства нулю линейной комбинации этих векторов
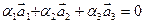
или в развёрнутом виде

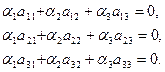
Если эти равенства выполняются при условии, что хотя бы один из коэффициентов 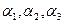 отличен от нуля, то векторы линейно зависимы. Записанные равенства представляют собой однородную систему линейных уравнений относительно коэффициентов
отличен от нуля, то векторы линейно зависимы. Записанные равенства представляют собой однородную систему линейных уравнений относительно коэффициентов 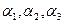 . Эта система имеет нетривиальное решение (т.е. решение, в котором не все
. Эта система имеет нетривиальное решение (т.е. решение, в котором не все
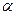 одновременно равны нулю) только при условии равенства нулю определителя системы. В рассматриваемом случае определитель системы равен
одновременно равны нулю) только при условии равенства нулю определителя системы. В рассматриваемом случае определитель системы равен
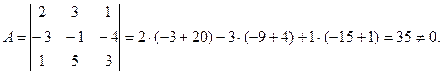 Таким образом система имеет лишь тривиальное решение и исходная совокупность векторов линейно независима.
Таким образом система имеет лишь тривиальное решение и исходная совокупность векторов линейно независима.
2. При каких 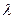 вектор
вектор 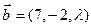 линейно выражается через векторы
линейно выражается через векторы
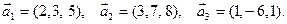
Решение. По условию задачи надо найти такие 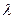 , при которых выполняется равенство
, при которых выполняется равенство
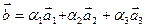
или в развёрнутом виде
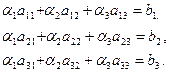
Записанные соотношения представляют собой систему неоднородных линейных уравнений относительно 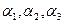 - коэффициентов линейной комбинации. В соответствии с теоремой Кронекера-Капелли эта система совместна, если ранг основной матрицы системы равен рангу расширенной матрицы. Выпишем расширенную матрицу для заданных условий:
- коэффициентов линейной комбинации. В соответствии с теоремой Кронекера-Капелли эта система совместна, если ранг основной матрицы системы равен рангу расширенной матрицы. Выпишем расширенную матрицу для заданных условий:

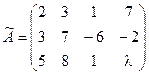
Сначала определим ранг основной матрицы. Видно, что отличные от нуля миноры второго порядка в матрице имеются, например, минор, стоящий в левом верхнем углу. Вычислим теперь минор третьего по-
рядка (определитель) основной матрицы
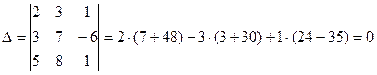 .
.
Следовательно, ранг основной матрицы равен двум. Таким образом рассматриваемая система будет совместна, если ранг расширенной матрицы
также будет равен двум. Для этого необходимо, чтобы второй минор третьего порядка расширенной матрицы был равен нулю, т.е.
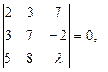
откуда следует
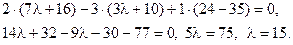
Задачи
3.7. Зависимы ли векторы
а) 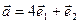 ,
, 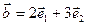 ;
;
б) 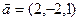 ,
, 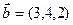 ,
, 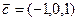 ;
;
в) 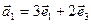 ,
, 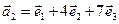 ,
, 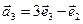 .
.
3.8. При каких значениях параметра 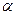 зависимы векторы
зависимы векторы
а) 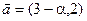 ,
, 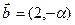 ;
;
б) 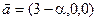 ,
,  ,
, 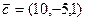 ;
;
в) 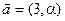 ,
, 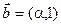 ,
, 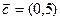 ;
;
г) 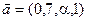 ,
, 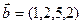 ,
, 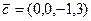 .
.
3.9. Является ли вектор 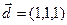 линейной комбинацией векторов
линейной комбинацией векторов 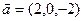 ,
, 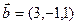 ,
, 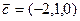 ?
?
3.10. Является ли вектор 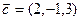 линейной комбинацией векторов
линейной комбинацией векторов
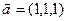 и
и 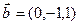 ?
?
3.11. При каких 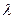 вектор
вектор 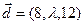 линейно выражается через векторы
линейно выражается через векторы 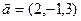 ,
, 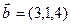 ,
, 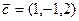 ?
?
3.12. При каких 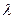 вектор
вектор 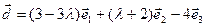 линейно выражается через векторы
линейно выражается через векторы 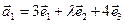 ,
, 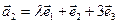 ,
, 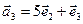 ?
?
3.13. Является ли линейно независимой система векторов в линейном пространстве квадратных матриц данного порядка:
a) 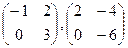 ;
;
b) 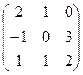 ,
, 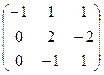 ,
, 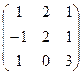 .
.
3.14. Является ли линейно зависимой система векторов в линейном пространстве многочленов степени не выше 2:
а) 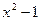 ,
,  ; б)
; б)  ,
, 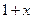 ,
, 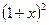 ;
;
в) 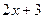 ,
, 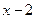 ,
, 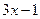 .
.
3.15. Является ли линейно независимой система векторов в линейном пространстве функций специального вида, заданных на указанном множестве:
а) 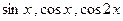 при
при 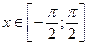 ;
;
б) 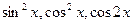 при
при 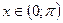 ;
;
в) 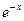 ,
,  ,
,  при
при 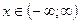 ;
;
г) 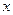 ,
, 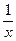 ,
,  при
при 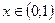 .
.
3.16. Доказать, что система векторов, содержащая нулевой вектор, всегда линейно зависима.
3.17. Доказать, что система векторов линейно зависима, если хотя бы один из этих векторов является линейной комбинацией остальных
векторов данной системы.
3.18. Доказать, что система векторов линейно независима, если ни один из этих векторов не является линейной комбинацией остальных векторов данной системы.
