Свойства дисперсии

1. Если k – число, то D[kx] = k² D[x], т.е. константа выносится из-под знака дисперсии с квадратом.

Докажем это.

D[kx] = M[(kx – M[kx])²] = M[(kx – k M[x])²] = M[k² (x – m_x)²] =

= k²M[x – m_x]² = k² D[x].

2. Сдвиг на константу не меняет дисперсии:

D[k+x]= D[x].

Свойства (1) и (2) объединяются в одно:

D[c+kx]= k²D[x].

3. Для попарно независимых случайных величин x₁, x₂,¼, x_n справедливо равенство

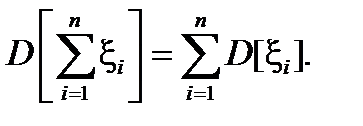
Пример 16. Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения:

X	–5
P	0,4	0,3	0,1	0,2

Решение. Дисперсию можно вычислить исходя из ее
определения, однако мы воспользуемся формулой D[X]=M[X²]–(M[X])², которая быстрее ведет к цели. Найдем математическое ожидание Х:

М[Х]=–5·0,4+2·0,3+3·0,1+4·0,2=–0,3.

Напишем закон распределения Х²:

X2
P	0,4	0,3	0,1	0,2

Найдем математическое ожидание Х²:

М[Х²]=25·0,4+4·0,3+9·0,1+16·0,2=15,3.

Вычислим искомую дисперсию:

.

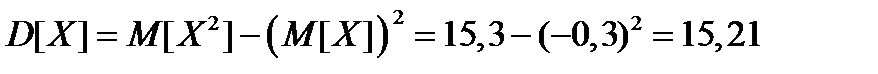и, наконец, искомое среднее квадратическое отклонение:

s_X= 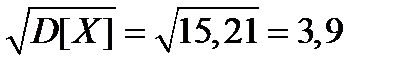.