Линейные уравнения с постоянными коэффициентами
Дифференциальное уравнение вида
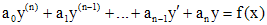 (1)
(1)
где 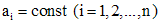 , f - известная функция, называется линейным дифференциальным уравнением n - го порядка с постоянными коэффициентами. Если
, f - известная функция, называется линейным дифференциальным уравнением n - го порядка с постоянными коэффициентами. Если 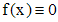 , то уравнение (1) называется однородным, в противном случае - неоднородным. К однородному уравнению, очевидно, применима теорема существования и единственности, причем интервалом определения решений этого уравнения будет вся действительная ось.
, то уравнение (1) называется однородным, в противном случае - неоднородным. К однородному уравнению, очевидно, применима теорема существования и единственности, причем интервалом определения решений этого уравнения будет вся действительная ось.
Если f - непрерывная функция, то общее решение уравнения (1) состоит из суммы общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения (1).
Чтобы решить однородное линейное уравнение с постоянными коэффициентами (1) надо составить характеристическое уравнение
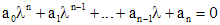 (2)
(2)
и найти его корни 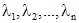 . Каждому простому корню
. Каждому простому корню 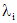 соответствует частое решение однородного уравнения (1), имеющее вид
соответствует частое решение однородного уравнения (1), имеющее вид 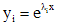 , а каждому корню
, а каждому корню 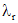 кратности k - решения
кратности k - решения 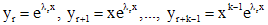 . Произвольная линейная комбинация всех частных решений является общим решением однородного уравнения (1), т.е.
. Произвольная линейная комбинация всех частных решений является общим решением однородного уравнения (1), т.е.
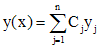 ,
,
где 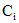 произвольные постоянные.
произвольные постоянные.
Если все коэффициенты однородного уравнения (1) вещественные, то решение можно написать в вещественной форме и в случае комплексных корней 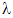 . Для каждой пары комплексно сопряженных корней
. Для каждой пары комплексно сопряженных корней 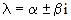 в формулу общего решения включаются слагаемые
в формулу общего решения включаются слагаемые
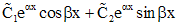 ,
,
если эти корни простые, и слагаемые
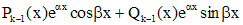 ,
,
если каждый из корней 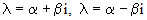 имеет кратность k. Здесь
имеет кратность k. Здесь 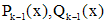 - многочлены степени k-1.
- многочлены степени k-1.
Пример 1.Решить уравнение 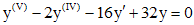 .
.
Решение.
Выпишем характеристическое уравнение, соответствующее данному однородному уравнению
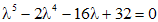 .
.
Разлагая левую часть уравнения на множители, находим корни:
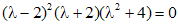 ,
,
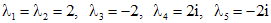 .
.
Следуя выше изложенной теории, выпишем общее решение данного уравнения
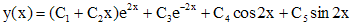 .
.
Для линейных неоднородных уравнений с постоянными коэффициентами и с правой частью специального вида, а именно состоящей из сумм и произведений функций 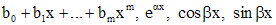 , частное решение можно искать методом неопределенных коэффициентов. Вид частного решения зависит от корней характеристического уравнения. Ниже представлена таблица видов частных решений линейного неоднородного уравнения с правой частью специального вида.
, частное решение можно искать методом неопределенных коэффициентов. Вид частного решения зависит от корней характеристического уравнения. Ниже представлена таблица видов частных решений линейного неоднородного уравнения с правой частью специального вида.
| Правая часть | Число, сравниваемое с корнем характеристического уравнения | Вид частного решения |
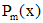 | 0 - не корень | 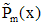 |
| 0 - корень кратности k | 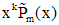 | |
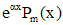 | 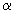 - не корень - не корень | 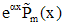 |
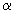 - корень кратности k - корень кратности k | … | |
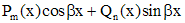 | 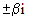 - не корень - не корень | 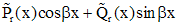 |
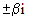 - корень кратности k - корень кратности k | 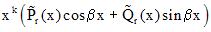 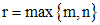 | |
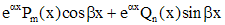 | 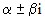 - не корень - не корень |  |
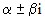 - корень кратности k - корень кратности k | 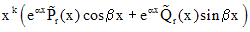 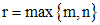 |
Здесь 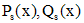 -многочлены степени s, а
-многочлены степени s, а 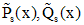 - многочлены степени s, коэффициенты которых нужно найти методом неопределенных коэффициентов. Для того чтобы их найти, нужно функцию, задающую вид частного решения, подставить в исходное дифференциальное уравнение и после приведения подобных слагаемых приравнять соответствующие коэффициенты в правой и левой частях уравнения. В случае, когда для определения вида частного решения нельзя воспользоваться только одной строкой таблицы, применяют принцип суперпозиции.
- многочлены степени s, коэффициенты которых нужно найти методом неопределенных коэффициентов. Для того чтобы их найти, нужно функцию, задающую вид частного решения, подставить в исходное дифференциальное уравнение и после приведения подобных слагаемых приравнять соответствующие коэффициенты в правой и левой частях уравнения. В случае, когда для определения вида частного решения нельзя воспользоваться только одной строкой таблицы, применяют принцип суперпозиции.
Теорема (принцип суперпозиции). Пусть 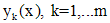 - решения уравнений
- решения уравнений
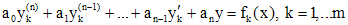 ,
,
соответственно. Тогда
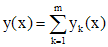
есть решение уравнения
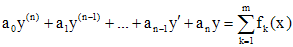 .
.
Пример 2.Решить уравнение 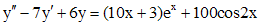 , удовлетворяющее условиям
, удовлетворяющее условиям 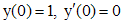 .
.
Решение.
Сначала найдем общее решение данного неоднородного уравнения второго порядка, а затем среди всех решений выберем то, которое удовлетворяет заданным условиям. Так как характеристическое уравнение 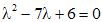 имеет корни
имеет корни 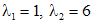 , то общим решением соответствующего однородного уравнения является функция:
, то общим решением соответствующего однородного уравнения является функция:
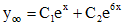 .
.
Правая часть исходного неоднородного уравнения представляет собой сумму двух функций специального вида 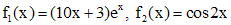 . Найдем методом неопределенных коэффициентов частные решения
. Найдем методом неопределенных коэффициентов частные решения 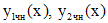 уравнений
уравнений
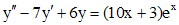 (*)
(*)
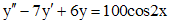 (**)
(**)
соответственно.
Определим частное решение 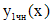 уравнения (*). Правая часть
уравнения (*). Правая часть 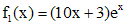 представляет собой произведение многочлена первой степени и
представляет собой произведение многочлена первой степени и 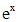 . Число, которое нужно сравнивать с корнем характеристического уравнения - это 1. Оно является простым корнем характеристического уравнения кратности 1. Согласуя с параметрами таблицы, имеем
. Число, которое нужно сравнивать с корнем характеристического уравнения - это 1. Оно является простым корнем характеристического уравнения кратности 1. Согласуя с параметрами таблицы, имеем 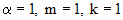 , следовательно, частное решение будем искать в виде:
, следовательно, частное решение будем искать в виде:
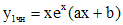 ,
,
где коэффициенты a и b подлежат определению. Подставляя последнее выражение в (*), и приравнивая коэффициенты при одинаковых степенях x в левой и правой частях, получим следующую систему:
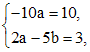
откуда 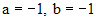 , а значит
, а значит
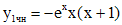 .
.
Правая 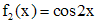 часть уравнения (**) представляет собой произведение многочлена нулевой степени и тригонометрической функции. Число 2i не является корнем характеристического уравнения. Частное решение
часть уравнения (**) представляет собой произведение многочлена нулевой степени и тригонометрической функции. Число 2i не является корнем характеристического уравнения. Частное решение 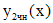 уравнения (**) ищем в виде (
уравнения (**) ищем в виде ( 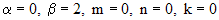 ):
):
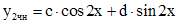 .
.
Подставляя 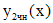 в (**), и приравнивая коэффициенты при sin2x и cos2x справа и слева, получим систему для определения коэффициентов c и d:
в (**), и приравнивая коэффициенты при sin2x и cos2x справа и слева, получим систему для определения коэффициентов c и d:
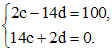
Откуда 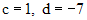 . Поэтому
. Поэтому 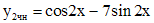 . Согласно принципу суперпозиции, частное решение
. Согласно принципу суперпозиции, частное решение 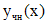 первоначального уравнения имеет вид:
первоначального уравнения имеет вид:
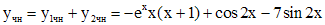 ,
,
а его общее решение определяется функцией:
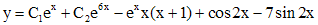 .
.
Чтобы решить задачу Коши, определим значения произвольных постоянных 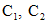 в общем решении. Для этого в решение и его производную подставим x=0. Используя начальные условия
в общем решении. Для этого в решение и его производную подставим x=0. Используя начальные условия 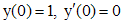 , получим:
, получим:
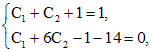
откуда 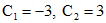 . Значит решение поставленной задачи Коши есть
. Значит решение поставленной задачи Коши есть
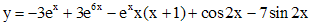 .
.
Линейное неоднородное уравнение (1) с любой правой частью 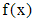 можно решить методом вариации постоянных. Пусть найдено общее решение
можно решить методом вариации постоянных. Пусть найдено общее решение 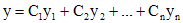 соответствующего линейного однородного уравнения. Тогда решения уравнения (1) ищется в виде
соответствующего линейного однородного уравнения. Тогда решения уравнения (1) ищется в виде
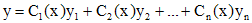 .
.
Функции 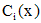 определяются из системы
определяются из системы
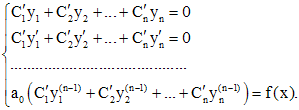
Пример 3.Решить уравнение 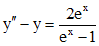 .
.
Решение.
Исходное уравнение есть линейное неоднородное уравнение второго порядка. Решим соответствующее однородное уравнение 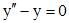 . Характеристическое уравнение для данного однородного уравнения есть
. Характеристическое уравнение для данного однородного уравнения есть 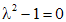 , решениями которого являются
, решениями которого являются 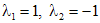 . Тогда общим решением однородного уравнения будет функция
. Тогда общим решением однородного уравнения будет функция 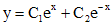 . Тогда решение заданного уравнения будем искать в виде
. Тогда решение заданного уравнения будем искать в виде
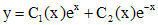 .
.
Функции 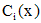 определяются из системы
определяются из системы
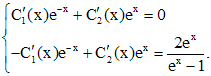
Решая систему, находим
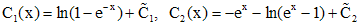 .
.
Тогда функция
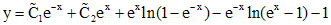
определяет общее решение исходного уравнения.
Рассмотрим дифференциальные уравнения, сводящиеся к линейным уравнения с постоянными коэффициентами.
