Линейные дифференциальные уравнения с постоянными коэффициентами

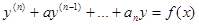где а₁…а_n - константы.

1) Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. 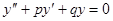где p, q = const его линейно независимые решения будем искать в виде 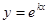, 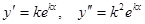и подставляем в однородное дифференциальное уравнение: 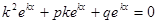, 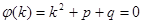характеристическое уравнение. Оно имеет два корня К₁ и К₂ – либо действительных либо комплексные – сопряженные.

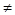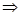
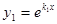а) К₁, К₂ – действительные и К₁ К₂ и 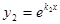- линейно независимые решения и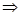

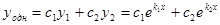
б) К1 и К2 – действительные и К₁=К₂ 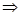их кратность r=2 и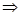 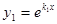Второе линейно независимое решение однородного дифференциального уравнения будем искать в виде 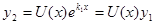тогда находим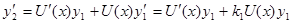

;

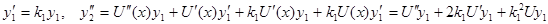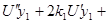
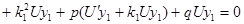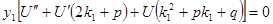; если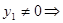

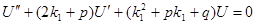но k₁ – корень характеристического уравнения то есть 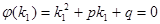, более того k₁ – корень кратности r=2 то есть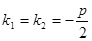

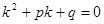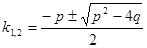( ; ) то есть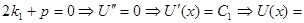

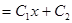Нам нужно выбрать С₂=0 и С₁=1

U_max: 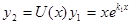в случае r=2 то есть 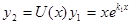где r>2 Þ 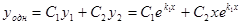при k₁=k₂

в) k₁ и k₂ – комплексно сопряженные корни то есть 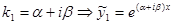и и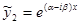ли два действительных линейно независимых решения ,

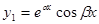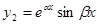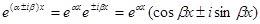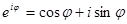; ; - формула Эйлера.

Общее решение: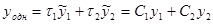

2)Линейные однородные дифференциальные уравнения n-ного порядка с постоянными коэффициентами. 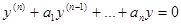где а₁, а₂ = const Его линейно независимое решение ищут в виде 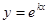После подстановки его в однородное дифференциальное уравнение получают характеристическое уравнение для к:

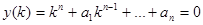это алгебраическое уравнение n-ного порядка и Þ имеет ровно n корней, включая комплексно сопряжённые, с учётом их кратностей. При этом могут представиться следующие четыре случая:

а) Каждому действительному корню k_i кратности =1, соответствует решение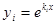

б) Каждому действительному корню k_j кратности r соответствует r линейно независимых решений: ; ; … ;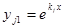

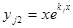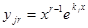
в) Каждой паре комплексно сопряжённых корне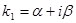й и 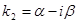кратности каждой r=1 соответствуют два линейно независимых решения 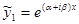и и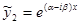ли два действительных линейно независимых решения 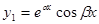и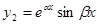

г) Каждой паре комплексно сопряжённых корне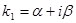й и 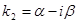кратности m соответствует 2m линейно независимых решен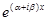и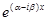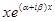й: и 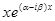; 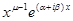и ;…; и 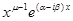или 2m действительных линейно независимых решен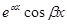и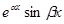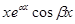й: и 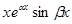; 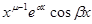и ;…; и .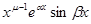

Линейные неоднородные дифференциальные уравнения n^-го порядка.

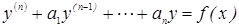. Для его решения вначале находят общее решение однородного уравнения затем находят частное решение неоднородного, тогда общее решение неоднородного уравнения представляют в виде суммы решений однородного и частного неоднородного т. е. 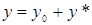, где у₀ – общее решение однородного дифференциального уравнения, у* - частное решение неоднородного дифференциального уравнения. Теорема: Если 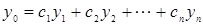есть общее решение однородного дифференциального уравнения 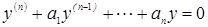, а у* - частное решение неоднородного дифференциального уравнения 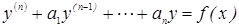то общее решение у неоднородного дифференциального уравнения представляется в виде суммы этих уравнений, т. е. 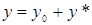. Доказательство: Доказательство проведем для случая n=2, 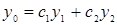- общее решение однородного дифференциального уравнения, а у* - частное решение неоднородного дифференциального уравнения 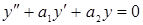. (а) Докажем, что 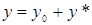решение неоднородного дифференциального уравнения следовательно

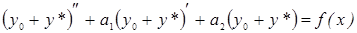или

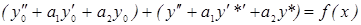(т.к. 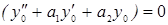- у₀ – общее решение однородного дифференциального уравнения, а 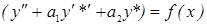- у* частное решение неоднородного дифференциального уравнения). 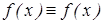. (б) Докажем, что у=у₀+у* общее решение неоднородного дифференциального уравнения т. е. удовлетворяет произвольным начальным условиям 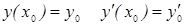отсюда следует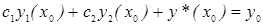

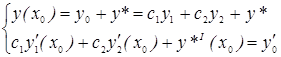или

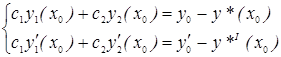эта система двух линейных неоднородных уравнений имеет единственное решение, если ее определитель 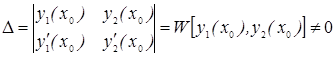, в точке х₀ , т.к. 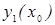и 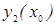- линейно независимы. Общих методов нахождения всех линейно независимых решений однородного дифференциального уравнения не существует исключения составляет только однородные дифференциального уравнения с постоянными коэффициентами если же общее решение однородного дифференциального уравнения известно 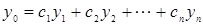, то общее решение неоднородного дифференциального уравнения (а следовательно и у*) может быть найдено методом вариаций произвольных постоянных, для этого общее решение неоднородного дифференциального уравнения ищут в виде 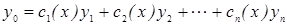, далее находят 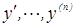и накладывают (n-1) дополнительных условий связывающие функции 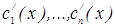и подставляют производные 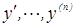, в исходное неоднородное дифференциальное уравнение. Объединяя полученные (n-1) дополнительных условий связывающие функции 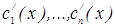и последнее выражение, получают систему n линейных уравнений относительно функций 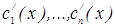и решая которую находят функцию 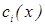. Интегрирую подставляя в 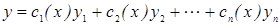находят общее решение. Выпишем систему: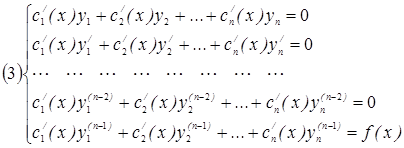

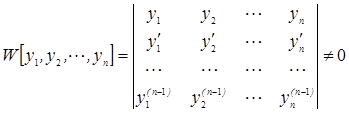, эта система имеет единственное решение. Докажем для случая n=2: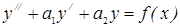

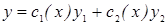
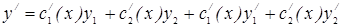и проинтегрируем полученное выражение: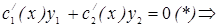 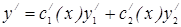отсюда находим 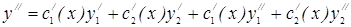подставляем 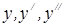в неоднородное дифференциальное уравнения:

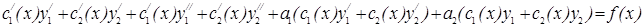
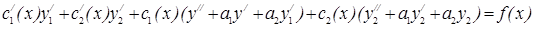следовательно мы получаем: 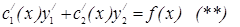Из (*) и (**)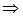

Замечание: Система (3) и (4) имеет смысл если коэффициент при 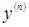в неоднородном дифференциальном уравнении равен 1.

Замечание:Если правая часть неоднородного дифференциального уравнения функция f(x) представляет собой сумму нескольких функций т.е. например 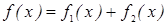, то частное решение у* соответствующей функции f(x) имеет также в виде у*=у₁*+у₂*, где у₁* соответствует правой части f₁(x),а у₂* соответственно f₂(x) (следует линейность дифференциального уравнения).