Первый и второй замечательный предел

Первый замечательный предел: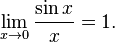

Второй замечательный предел: 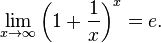или

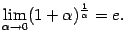
Вопрос 15.

Непрерывность функции в точке,в интервале,на отрезке.
Функция y=f(x),наз-ся непрерывной в т.x₀,если сущ предел ф-ции в этой точке и он равен значению ф-ции в этой точке. 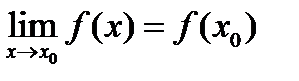(1) равенство (1) означает выполнение 3-х усл:

1)ф-я опред в т Хо и ее окрестности

2)ф-я f(x) имеет lim x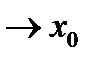

3)lim f(x) в т.Хо=ее значению в этой точке

Пусть y=f(x) опред в некотором (a;b) возьмем т.Хo 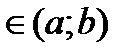.Для любого Х 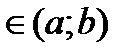разность x 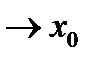, назыв приращением аргументов Х в т.Хо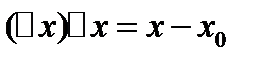

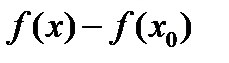Разность,назыв приращением ф-ции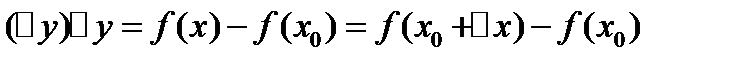

2 опред неприрывности

Усл 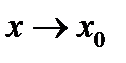и 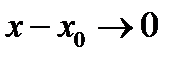одинаковые 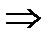равенство(1) принимает вид: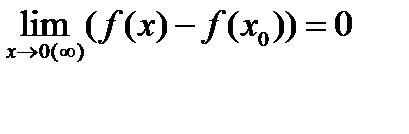

(2)

Т.е ф-я y=f(x),назыв неприрывной в т.Хо,если она опред в т.Хо и ее окрестности выполняется равенство (2),т.е БМ приращению аргумента соответ БМ приращению ф-ции

Ф-ция y=f(x),наз-ся непрерывной на интервале (a;b),если она непрерывна в каждой т.этого интервала.
y=f(x),наз-ся непрерывной на отрезке [a;b],если она непрерывна на интервале (a;b) и в т. X=a и справа это значит 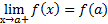,а в т.x=b непрерывна слева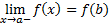
Точки в которой нарушается непрерывность ф-ции наз-ся точками разрыва этой ф-ции.Если x= x₀,-т.разрыва функции,то в ней не выполняется одно из 3х усл.непрерывности.

Вопрос 16.

Точки в Х нарушается неприрывность ф=ции,назыв точками разрыва этой ф-ции,если Х=Хо точка разрыва ф-ции,то в ней не выполнится одно из 3-х усл неприрывности.

Точки разрыва ф-ции и их классификация
Все т.разрыва ф-ции подразделяются на т.разрыва 1-го и 2-го порядка.
т.разрыва x₀-т.разрыва 1 рода, ф-ции y=f(x),если существует в этой т.конечный левый и правый пределы 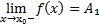, 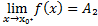При этом:
а)если А₁=А₂ , то x₀ - т.устраненного разрыва
б)если A₁≠A₂ ,то x₀ - т.конечного разрыва. Вел-на модуля |А₂-А₁|, скачок ф-ции, т.разрыва 1 рода.

Т.разрыва, x₀ наз-ся т.разрыва 2го рода ф-ции y=f(x) если по крайней мере 1 из односторонних пределов =∞ или не сущ.

Вопрос 17.Основные теоремы о непрерывных ф-циях.
1.Сумма произведения частное 2х непрерывных функций есть непрерывная функция.
2.Пусть ф-ция u= 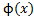непрерывна в т. x₀,а ф-ция y=f(u) непрерывна в т. u₀=ϕ(x₀) тогда сложная ф-ция y=( ϕ(x))-непрерывна в т. x₀
3.Все элементарные ф-ции непрерывны для всех значений Х входящих в область их определения.

Вопрос 18.

Задачи приводящие к понятию производной.

Пусть материальная т.М движется не равномерно по прямой

Каждому моменту времени t соответствует расстояние OM=S.Это расстояние зависит от времени s=s(t).Равенство назыв законом движения точки.

Найдем скорость движения точки .

Пусть момент времени 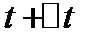,точка займет положение 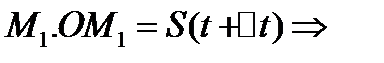переменная т.М за время 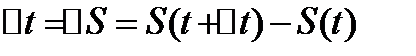.Отношение 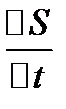назыв средней скоростью движения точки за время 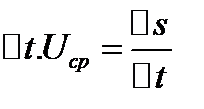Предел 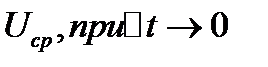назыв скоростью движения точки в момент времени t(мгновенною скоростью)

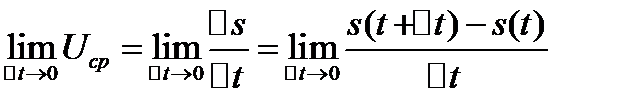
Касательная кривой

Возьмем на кривой L 2 точки M и 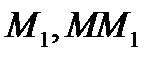назыв секущей. Пусть т. 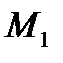двигаясь вдоль кривой L приближается к т.М , когда тогда секущая поворачивается вокруг т.М и стремится к некоторому предельному положению МТ. Касательной к данной кривой данной т.М назыв предельное положение МТ секущей 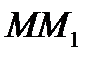,проходящей через т.М и 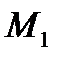,когда т. 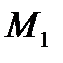неограниченно приближается по кривой к т.М

Рассмотрим неприрывну ф-цию y=f(x).

Проведем касательн к графику в этой точки и обозначим углом образован этой касательн с положит направлен ОХ,угловой коэф этой касат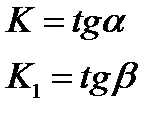

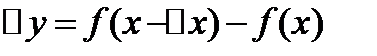
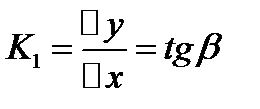
При 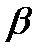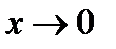,т. 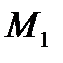будет неограниченно приближаться по кривой к т.М,а секущая будет поворачиваться вокруг т.М переходя в касательную ,а 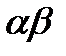будет стремится к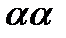

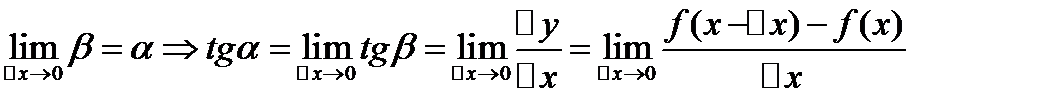=углов коэф к касат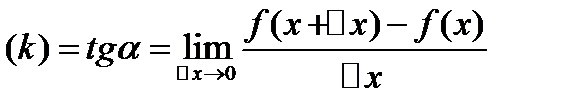
Вопрос19.

Определение производной,её механический и геометрический смысл.Связь между непрерывностью и дифференцируемостью функции.
Пусть ф-ция y=f(х) определенна в интервале (a;b)
1.аргументу хͼ(a;b) придадим приращение х такое,что 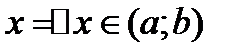2.найдем соотв.приращение ф-ции y. ∆y=f(x+∆x)-f(x)
3.сост.отнош.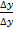
4.и перейдем к пределу этого отнош.при ∆х->0

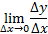Если этот предел существует,то он наз-ся производной ф-ции f(x) и обозначается f’’х, f’ (x),y’(x) и т.д.
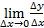= f’ (x)
Производной ф-ей y=f(x) в т.Хо назыв предел отношения,приращение ф-ции приращения аргумента ,когда последнее .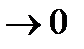

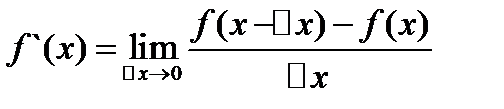
Операция нахождения производ-дифференцированием .Если ф-ция y=f(x) имеет производ в каждой т.(a;b),то она назыв дифференцированной на (а;b)

Др.обозначения произв в т.y`(Xo);

Рассмотрим мгновенную скорость

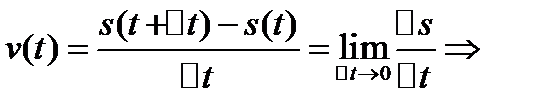это равенство можно написать в виде v`(t)=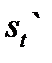

Скорорсть прямолинейнного движения материальной точки в момент t есть производ пути S по времени t-в этом физический смысл.

Рассмотрим улговой коэф касательной.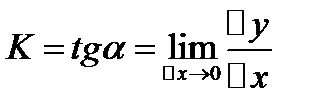

По определен производ K=f`(x)

Производн ф-ции в т.Х=углов коэф касат проведенной к графику ф-ции в т.Х-геометр смысл.?????

Связь между непрерывностью и дифференцируемостью функции.
Теорема:Если ф-ция дифф-ая в некоторой точки,то она неприрывна в этой точки

Теорема не верна:неприрывная ф-ция может не иметь производной.

Вопрос 20.

Правила дифференцирования.Формулы деференцирования
Рассмотрим ф-ции u=u(x),v=v(x)
1.(v±u)ˈ=(uˈ±vˈ)
2.(uv)ˈ=uˈv+vˈu (cuˈ)cuˈ -постоянную можно вынести за знак
3.( )ˈ=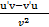

4.Сложной функции
y=f(u) u=ϕ(x)

yᵪˈ=yˈᵤ · Uₓ

5.Связь между кривой произв-ой обратной ф-ции:

y=f(x), x=ϕ(y)

yₓˈ=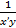

Формулы дифференцирования

1.(c)ˈ=0 c-const

2.( 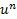)ˈ=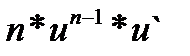

2. ( a ^u )' = a ^u lna ×u'.

3. ( e ^u )' = e ^u u'.

4. (log _a u)' = u' /( u ln a).

5. (ln u)' = u'/u.

6. ( sin u)' = cos u ×u'.

7. (cos u)' = - sin u ×u'.

8. (tg u)' = 1/ cos ² u ×u'.

9. ( ctg u)' = - u' / sin ² u.

10. (arcsin u)' = u' / .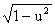

11. ( arccos u)' = - u' / .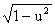

12. (arctg u)' = u' /( 1 + u ² ).

13. (arcctg u)' = - u' /( 1 + u ² ).

Вопрос 21.

Дифференцтрование неявных функций, Если ф-ия задана ур-ем y=f(x), разрешееном относит. у, то эта ф-ия задана в явном виде. Не явно заданная ф-ия задается ур-ем не разрешенном относит. у. Для нахождения ее производной нужно продефферен. ее ур-е F(x;y)=0 по х. Рассматривая у как ф-ию х. Из полученного ур-я выразить у^’.